В третьем задании ЕГЭ по профильной математике рассматривается стереометрия, объемные фигуры. Для вас задания из открытого банка ФИПИ с ответами. Все из нового банка, все задания могут попасться на реальном ЕГЭ. КЭС: Геометрия
Все задания из ОБОИХ банков ФИПИ. 36 заданий из нового банка, остальные 350 из старого.
Задания по стереометрии с ФИПИ, ЕГЭ мат профиль
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 5√2 . Найдите площадь боковой поверхности конуса.
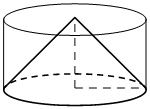
КЭС: 5.4 Тела и поверхности вращения 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение:
5
Площадь боковой поверхности цилиндра
Sц=2πrh=2πr2=5√2
Площадь поверхности конуса
Sк=πrl
При этом
l2=r2+r2
`l=sqrt(2r^2)`=r√2
Sк=πr*r√2=(2*πr*r√2)/2= (5√2*√2)/2=5
Ответ: 5
Номер: 37164B
Впишите правильный ответ.
Найдите объём многогранника, вершинами которого являются вершины A , B , C , C1 правильной треугольной призмы ABCA1B1C1 , площадь основания которой равна 6, а боковое ребро равно 9.
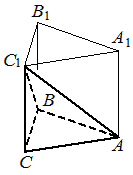
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
18
ABCC1 это пирамида, объем которой равен 1/3*Sоснования *h
Объем призмы равен Sоснования *h, то есть пирамида по объему в три раза меньше, тогда
`(6*9)/3`=18
Ответ:18
Номер: BE03FA
Впишите правильный ответ.
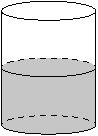
Шар, объём которого равен 18, вписан в цилиндр. Найдите объём цилиндра.
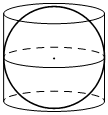
КЭС: 5.4 Тела и поверхности вращения 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
27
Объем шара
V=4/3*π*r3
Объем цилиндра
V=2π*r*h
h=2r, тогда
V=π*r2*2r=2π*r3
Объемы относятся как 4/3 и 2
То есть объем цилиндра больше в 2:4/3=1,5 раза
18*1,5=27
Ответ: 27
Номер: 6D5AF2
Впишите правильный ответ.
Найдите объём многогранника, вершинами которого являются вершины A , B , C , D , B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=9, BC=3, BB1=8 .
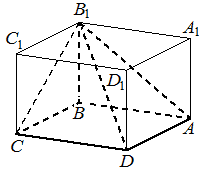
КЭС: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
72
ABCDB1 это пирамида, объем которой равен 1/3*Sоснования *h
Объем параллелепипеда равен Sоснования *h, то есть пирамида по объему в три раза меньше, тогда
`(3*9*8)/3`=72
Ответ: 72
Номер: 29FE0E
Впишите правильный ответ.
Через среднюю линию основания треугольной призмы, объём которой равен 52, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.
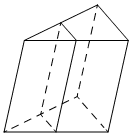
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
13
Соотношение объемов между треугольными призмами будет равно соотношению площади треугольников, так как они являются площадью основания, а высота у них одинаковая.
Причем так как это средняя линия, то она меньше основания треугольника в 2 раза, и высота треугольника тоже меньше в 2 раза, то есть площадь треугольников соотносится как 1/4
`52/4`=13
Ответ:13
Номер: 5C9973
Впишите правильный ответ.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсечённой треугольной призмы равен 15.

КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
60
Соотношение объемов между треугольными призмами будет равно соотношению площади треугольников, так как они являются площадью основания, а высота у них одинаковая.
Причем так как это средняя линия, то она меньше основания треугольника в 2 раза, и высота треугольника тоже меньше в 2 раза, то есть площадь треугольников соотносится как 1/4
15*4=60
Ответ: 60
Номер: 817F71
Впишите правильный ответ.
Дана правильная треугольная призма ABCA1B1C1 , площадь основания которой равна 8, а боковое ребро равно 6. Найдите объём многогранника, вершинами которого являются точки A , C , A1 , B1 , C1 .
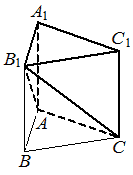
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
32
BACB1 это пирамида, объем которой равен 1/3*Sоснования *h
Объем призмы равен Sоснования *h, то есть пирамида по объему в три раза меньше, тогда
`8*6/3`=16
Но в нашем случае объем ACA1B1C1 находится как разность объемов пирамиды и призмы. 48-16=32
Ответ: 32
ИЛИ
BACB1 - это пирамида, объем которой равен `1/3*S_(основания) *h`
Объем призмы равен `S_(основания)*h`.
`V_(приз.)=8*6=48`
`V_(ABCB_1)=1/3*8*6=16`
Объем ACA1B1C1 находится как разность объемов призмы и пирамиды
`V=48-16=32`
Ответ: 32
Номер: F277BE
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=6 , BC=5 , AA1=4. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1 .

КЭС: 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
20
Объем A B C B1 составляет 1/6 от ABCDA1B1C1D1, так как это пирамида V=1/3 * Sосн. * h
в то время как параллелепипед V= Sосн. * h, то есть здесь при том же основании пирамида меньше параллелепипеда в три раза.
Да к тому же еще и площадь основания меньше в 2 раза, так как делится по диагонали. В итоге 2*3=6 во столько раз соотносятся объемы фигур.
тогда
`(6*5*4)/6`=20
Ответ: 20
Номер: B28DB5
Впишите правильный ответ.
Через среднюю линию основания правильной треугольной призмы, объём которой равен 84, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.
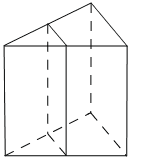
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
21
Соотношение объемов между треугольными призмами будет равно соотношению площади треугольников, так как они являются площадью основания, а высота у них одинаковая.
Причем так как это средняя линия, то она меньше основания треугольника в 2 раза, и высота треугольника тоже меньше в 2 раза, то есть площадь треугольников соотносится как 1/4
тогда `84/4`=21
Ответ:21
Номер: 6F27B9
Впишите правильный ответ.
Дано два цилиндра. Объём первого цилиндра равен 15. У второго цилиндра высота в 3 раза меньше, а радиус основания в 2 раза больше, чем у первого. Найдите объём второго цилиндра.
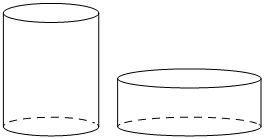
КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
20
Объем цилиндра
V=πr2*h
Если высота в 3 раза меньше, то она уменьшает объем в 3 раза, а если радиус основания в 2 раза больше, то он увеличивает объем в 4 раза, так как 2r в квадрате даcт значение 4r2
Итого 4/3, во столько должен отличаться объем второго цилиндра от первого.
`(15*4)/3`=20
Ответ:20
Номер: F4F51D
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 30. Найдите объём конуса.
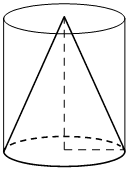
КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
10
Объем цилиндра
Vц=πr2h=30
Объем конуса
Sк=1/3πr2h
То есть объем конуса в 3 раза меньше цилиндра в который он вписан.
`30/3`=10
Ответ:10
Номер: 26B211
Впишите правильный ответ.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 60. Найдите объём конуса.
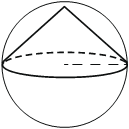
КЭС: 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
15
Объем шара
Vш=4/3*πr3=60
Объем конуса
Sк=1/3*πr2h=1/3*πr2*r=1/3*πr2*r
То есть объем конуса и шара соотносятся как величины 4/3 к 1/3.
4/3:1/3=12/3=4 раза
Находим объем конуса
`60/4`=15
Ответ:15
Номер: 80631B
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=7 , BC=6 , AA1=5 . Найдите объём многогранника, вершинами которого являются точки A , B , C , B1 .
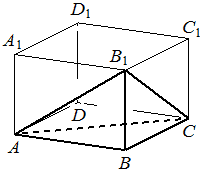
КЭС: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
35
Объем ABCB1 составляет 1/6 от ABCDA1B1C1D1, так как это пирамида V=1/3 * Sосн. * h
в то время как параллелепипед V= Sосн. * h, то есть здесь при том же основании пирамида меньше параллелепипеда в три раза.
Да к тому же еще и площадь основания меньше в 2 раза, так как делится по диагонали. В итоге 2*3=6 во столько раз соотносятся объемы фигур.
тогда
`(6*7*5)/6`=35
Ответ:35
Номер: 06E32C
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BC=9, CD=3, CC1=7. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, C1.
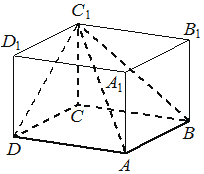
КЭС: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
63
ABCDB1 это пирамида, объем которой равен 1/3*Sоснования *h
Объем параллелепипеда равен Sоснования *h, то есть пирамида по объему в три раза меньше, тогда
`(3*9*7)/3`=63
Ответ: 63
Номер: 2D6929
Впишите правильный ответ.
Во сколько раз уменьшится объём конуса, если его высота уменьшится в 9 раз, а радиус основания останется прежним?
КЭС: 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
9
Объем конуса
Sк=1/3πr2h
Если уменьшим высоту в 9 раз, то получим Sк=1/3*π*r2*h/9 то есть уменьшится в 9 раз
Ответ:9
Номер: E71725
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=5 , BC=4 , AA1=3 . Найдите объём многогранника, вершинами которого являются точки A , B , C , D , A1 , B1 .

КЭС: 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
30
ABCDA1B1 объем равен 1/2*Sоснования *h
Объем параллелепипеда равен Sоснования *h, то есть пирамида по объему в два раза меньше, тогда
`(5*4*3)/2`=30
Ответ: 30
ИЛИ
Объем параллелепипеда
V = abh
`V =1/2*V_(пар)=1/2*3*4*5=30`
Ответ: 30
Номер: 32AF22
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 6. Найдите объём конуса.

КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
2
Объем цилиндра
Vц=πr2h=6
Объем конуса
Sк=1/3πr2h
То есть объем конуса в 3 раза меньше цилиндра в который он вписан.
`6/3`=2
Ответ:2
Номер: 41E054
Впишите правильный ответ.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
12
Соотношение площадей боковых сторон между треугольными призмами будет равно соотношению площади оснований, боковых сторон, и все они соотносятся между собой как 1/2. Так как высота и образующая меньше в два раза и средняя линия по сравнению с основанием тоже меньше в 2 раза.
Тогда `24/2`=12
Ответ:12
Номер: 1F4550
Впишите правильный ответ.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 12. Найдите объём шара.

КЭС: 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
48
Объем шара
Vш=4/3*πr3
Объем конуса
Sк=1/3*πr2h=1/3*πr2*r=1/3*πr2*r = 12
То есть объем конуса и шара соотносятся как величины 4/3 к 1/3.
4/3:1/3=12/3=4 раза
Находим объем шара
12*4=48
Ответ:48
Номер: 1D9551
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 6. Найдите объём цилиндра.

КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
18
Объем цилиндра
Vц=πr2h=6
Объем конуса
Sк=1/3πr2h
То есть объем конуса в 3 раза меньше цилиндра в который он вписан.
Тогда объем цилиндра 6*3=18
Ответ:18
Номер: DFC057
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9 , BC=7 , AA1=6 . Найдите объём многогранника, вершинами которого являются точки A , B , C , B1 .

КЭС: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
63
Объем A B C B1 составляет 1/6 от ABCDA1B1C1D1, так как это пирамида V=1/3 * Sосн. * h
в то время как параллелепипед V= Sосн. * h, то есть здесь при том же основании пирамида меньше параллелепипеда в три раза.
Да к тому же еще и площадь основания меньше в 2 раза, так как делится по диагонали. В итоге 2*3=6 во столько раз соотносятся объемы фигур.
тогда
`(9*7*6)/6`=63
Ответ:63
Номер: 467AAF
Впишите правильный ответ.
Шар, объём которого равен 24, вписан в цилиндр. Найдите объём цилиндра.

КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.4.3 Шар и сфера, их сечения 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
36
Объем шара
V=4/3*π*r3
Объем цилиндра
V=2π*r*h
h=2r, тогда
V=π*r2*2r=2π*r3
Объемы относятся как 4/3 и 2
То есть объем цилиндра больше в 2:4/3=1,5 раза
24*1,5=36
Ответ:36
Номер: 48EB9B
Объём куба равен 80. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Решение:
Отношение площадей `S_(больш.Δ)/S_(мал.Δ) = k^2`
1) Рассмотрим ABCD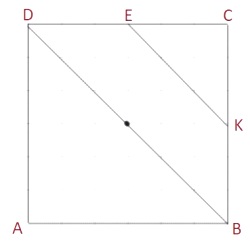
ΔCEK∼ΔBCD
`k=2`
`S_(BCD)/S_(CEK) = 2^2`
То есть в ΔBDC войдет 4 треугольника KEC, а в четырехугольник - 8 треугольников KEC.
`V_(приз)=1/8V_(куба)=1/8*80=10`
Ответ: 10
Номер: F51D9A
Впишите правильный ответ.
Дано два цилиндра. Объём первого цилиндра равен 18. У второго цилиндра высота в 3 раза меньше, а радиус основания в 2 раза больше, чем у первого. Найдите объём второго цилиндра.

КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
24
Объем цилиндра
V=πr2*h
Если высота в 3 раза меньше, то она уменьшает объем в 3 раза, а если радиус основания в 2 раза больше, то он увеличивает объем в 4 раза, так как 2r в квадрате даcт значение 4r2
Итого 4/3, во столько должен отличаться объем второго цилиндра от первого.
(18*4)/3=24
Ответ:24
Номер: 61D99A
Впишите правильный ответ.
Дана правильная треугольная призма ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 6. Найдите объём многогранника, вершинами которого являются точки B, C, A1, B1, C1.
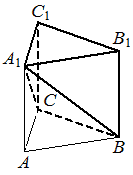
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
16
BACB1 это пирамида, объем которой равен 1/3*Sоснования *h
Объем призмы равен Sоснования *h, то есть пирамида по объему в три раза меньше, нам надо найти объем BCA1B1C1, он равен
`V_(ABCA1B1C1) - V_(BACB1)= V_(BCA1B1C1)`
1-1/3=2/3 от правильной треугольной призмы.
`4*6*2/3`= 16
Ответ:16
Номер: 370392
Впишите правильный ответ.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсечённой треугольной призмы равен 5.

КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
20
Соотношение объемов между треугольными призмами будет равно соотношению площади треугольников, так как они являются площадью основания, а высота у них одинаковая.
Причем так как это средняя линия, то она меньше основания треугольника в 2 раза, и высота треугольника тоже меньше в 2 раза, то есть площадь треугольников соотносится как 1/4
тогда 5*4=20
Ответ:20
Номер: 0989E5
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=7 , BC=6 , AA1=5 . Найдите объём многогранника, вершинами которого являются точки A, B, C, A1, B1, C1.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
105
ABCA1B1C1 объем равен 1/2*Sоснования *h так как сечение проходит по диагонали основания и на всю высоту.
Объем параллелепипеда равен Sоснования *h, то есть пирамида по объему в два раза меньше, тогда
`(7*6*5)/2`=105
Ответ: 105
Номер: B1EBED
Впишите правильный ответ.
Найдите объём многогранника, вершинами которого являются вершины A , B , C , C1 правильной треугольной призмы ABCA1B1C1 , площадь основания которой равна 7, а боковое ребро равно 9.
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
21
BACB1 это пирамида, объем которой равен 1/3*Sоснования *h
Объем призмы равен Sоснования *h, то есть пирамида по объему в три раза меньше.
Найдем ее объем
`(7*9)/3`=21
Ответ:21
Номер: 2359E0
Впишите правильный ответ.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 36. Найдите площадь боковой поверхности исходной призмы.

КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение:
72
Соотношение площадей боковых сторон между треугольными призмами будет равно соотношению площади оснований, боковых сторон, и все они соотносятся между собой как 1/2. Так как высота и образующая меньше в два раза и средняя линия по сравнению с основанием тоже меньше в 2 раза.
Тогда 36*2=72
Ответ:72
Номер: 5C56EC
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна 3√2 . Найдите площадь боковой поверхности цилиндра.

КЭС: 5.4 Тела и поверхности вращения 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение:
6
Площадь боковой поверхности цилиндра
Sц=2πrh=2πr2
Площадь поверхности конуса
Sк=πrl=3√2
При этом
l2=r2+r2
`l=sqrt(2r^2)`=r√2
Sк=πr*r√2
то есть πr*r = 3, тогда объем цилиндра будет из формулы выше в 2 раза больше
3*2=6
Ответ:6
Номер: E45C62
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=6 , BC=5 , AA1=4 . Найдите объём многогранника, вершинами которого являются точки A , B , C , D , A1 , B1 .

КЭС: 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
60
ABCDA1B1 объем равен 1/2*Sоснования *h так как сечение проходит по диагонали боковой стороны и на всю ширину.
Объем параллелепипеда равен Sоснования *h, то есть пирамида по объему в два раза меньше, тогда
`(4*6*5)/2`=60
Ответ: 60
Номер: 793F38
Впишите правильный ответ.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9 , BC=6 , AA1=5 . Найдите объём многогранника, вершинами которого являются точки A , B , C , B1 .

КЭС: 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
45
Объем A B C B1 составляет 1/6 от ABCDA1B1C1D1, так как это пирамида V=1/3 * Sосн. * h
в то время как параллелепипед V= Sосн. * h, то есть здесь при том же основании пирамида меньше параллелепипеда в три раза.
Да к тому же еще и площадь основания меньше в 2 раза, так как делится по диагонали. В итоге 2*3=6 во столько раз соотносятся объемы фигур.
тогда
`(9*6*5)/6`=45
Ответ:45
Номер: E5413A
Впишите правильный ответ.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсечённой треугольной призмы равен 7.

КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
28
Соотношение объемов между треугольными призмами будет равно соотношению площади треугольников, так как они являются площадью основания, а высота у них одинаковая.
Причем так как это средняя линия, то она меньше основания треугольника в 2 раза, и высота треугольника тоже меньше в 2 раза, то есть площадь треугольников соотносится как 1/4
тогда 7*4=28
Ответ:28
Номер: 843F31
Впишите правильный ответ.
Цилиндр, объём которого равен 18, описан около шара. Найдите объём шара.

КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.4.3 Шар и сфера, их сечения 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
12
Объем шара
V=4/3*π*r3
Объем цилиндра
V=2π*r*h
h=2r, тогда
V=π*r2*2r=2π*r3
Объемы относятся как 4/3 и 2
То есть объем цилиндра больше в 2:4/3=1,5 раза
18/1,5=12
Ответ:12
Номер: B4FF85
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 18. Найдите объём конуса.

КЭС: 5.4 Тела и поверхности вращения 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
6
Объем цилиндра
Vц=πr2h=18
Объем конуса
Sк=1/3πr2h
То есть объем конуса в 3 раза меньше цилиндра в который он вписан.
`18/3`=6
Ответ: 6
Номер: D8F984
Впишите правильный ответ.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 9. Найдите объём цилиндра.

КЭС: 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развёртка 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
27
Объем цилиндра
Vц=πr2h
Объем конуса
Sк=1/3πr2h
То есть объем конуса в 3 раза меньше цилиндра в который он вписан.
то есть объем цилиндра 9*3=27
Ответ:27
Номер: C59282
Впишите правильный ответ.
Во сколько раз увеличится объём конуса, если радиус его основания увеличится в 11 раз, а высота останется прежней?

КЭС: 5.4.2 Конус. Основание, высота, боковая поверхность, образующая, развёртка 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
121
Объем конуса
Sк=1/3πr2h
Если увеличим радиус в 11 раз, то получим Sк=1/3*π*112r2h
11*11=121, то есть объем увеличится в 121 раз
Ответ:121
Номер: 33B18F
Задания из старого банка ФИПИ
Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).

Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 3*2*3-1*1*3=15
Ответ: 15
Номер: 79A288
Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).

Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 5*3*1-1*1*3=12
Ответ: 12
Номер: 0630DF
Найдите объём многогранника, изображённого на рисунке (все двугранные углы — прямые).

Решение:
...
Ответ:
Номер: 9F1158
Найдите объём многогранника, изображённого на рисунке (все двугранные углы — прямые).

Решение:
...
Ответ:
Номер: 5B434D
Найдите объём многогранника, изображённого на рисунке (все двугранные углы — прямые).

Решение:
...
Ответ:
Номер: 0A76AD
Найдите объём многогранника, изображённого на рисунке undefined (все двугранные углы многогранника прямые).

Решение:
...
Ответ:
Номер: 2685D2
Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).

Решение:
...
Ответ:
Номер: BEBEA0
Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).

Решение:
...
Ответ:
Номер: CE3CAC
Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).

Решение:
...
Ответ:
Номер: 7BEFC4
Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).

Решение:
...
Ответ:
Номер: 747A9F
Найдите объём многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=3, AD=4, AA1=5.
Решение:
Объем параллелепипеда V = abh
`V =1/2*V_(пар.)=1/2*3*4*5=30`
Ответ: 30
Номер: C352F6
В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 4. Найдите её объём.
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) ΔCOD
`OC=sqrt(4^2-2^2)=sqrt12=2sqrt3`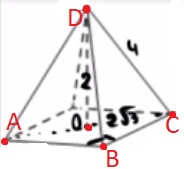
2) ΔABC:
`(4sqrt3)^2=x^2+x^2`
`48=2x^2`
`x^2=24`
3) `V=1/3*24*2=16`
Ответ: 16
Номер: F26E93
В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

Решение:
...
Ответ:
Номер: 22DBDC DF37FC
В правильной четырёхугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите её объём.

Решение:
...
Ответ:
Номер: 9C2BD6
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
Решение:
Обозначим стороны маленького треугольника за a b c
1) `S_(бок.пов.мал.) = ah+bh+ch=37`
2) `S_(бок.пов.бол.) = 2ah+2bh+2ch=2(ah+bh+ch)=2*37=74`
Ответ: 74
Номер: AB1F5D
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.

Решение:
...
Ответ:
Номер: A643C9
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.

Решение:
...
Ответ:
Номер: C93F05
Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
Решение:
Площадь поверхности конуса
`S = πR^2+πRl`
1) `K_(подобия конусов) = (5x)/(3x)=5/3=R_(бол)/R_(мал)=l_(бол)/l_(мал)`
2) `S_(пов. бол.) = 35=π(5/3R)^2+π*5/3*R*5/3*l`
`35=25/9*πR^2+25/9*πRl`
`35=25/9(πR^2+πRl)`
`πR^2+πRl = (35*9)/25=63/5=12,6`
3) `S_(пов. мал.) = πR^2+πRl=12,6`
Ответ: 12,6
Номер: 0C55B6
Площадь полной поверхности конуса равна 32,5. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 4:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
Решение:
Площадь боковой поверхности конуса
`S = πRl`
1) `K_(подобия конусов) = (5x)/(4x)=5/4=R_(бол)/R_(мал)=l_(бол)/l_(мал)`
2) `S_(пов. бол.) = 32,5=π(5/4R)^2+π*5/4*R*5/4*l`
`32,5=25/16*πR^2+25/16*πRl`
`32,5=25/16(πR^2+πRl)`
`πR^2+πRl = (32,5*16)/25=104/5`
3) `S_(пов. мал.) = πR^2+πRl=104/5=20,8`
Ответ: 20,8
Номер: 4F5B93
Площадь полной поверхности конуса равна 15. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 2:3, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

Решение:
...
Ответ:
Номер: 46716E
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 2 и 7, боковое ребро призмы равно 6. Найдите объём призмы.
Решение:
Площадь прямоугольного треугольника
`S=(ab)/2`
Объем призмы
`V = S_(осн)*h`
1)`S=(2*7)/2=7`
2)`V = 7*6=42`
Ответ: 42
Номер: C2CADE
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 3 и 4, боковое ребро призмы равно 4. Найдите объём призмы.

Решение:
...
Ответ:
Номер: 474C30
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 7, объём призмы равен 56. Найдите боковое ребро призмы.

Решение:
Площадь прямоугольного треугольника
`S=(ab)/2`
Объем призмы
`V = S_(осн)*h`
1) `S=(4*7)/2=14`
2)`56 = 14*h`
`h = 4`
Ответ: 4
Номер: 872654
В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
Решение:
Объем цилиндра
`V=πR^2h`
Радиус окружности, описанной около прямоугольного треугольника
`R=c/2`, где с - гипотенуза и диаметр
ΔABC - треугольник в основании призмы
1) ΔABC:
`AB=sqrt(10^2+9^2)=sqrt181`
2) `R=sqrt181/2`
3) `V_ц=π*(sqrt181/2)^2*2/π=181/4*2=90,5`
Ответ: 90,5
Номер: E7964C
В правильной шестиугольной пирамиде боковое ребро равно 6,5, а сторона основания равна 2,5. Найдите высоту пирамиды.
Решение:
Радиус окружности, описанной около равностороннего шестиугольника, равен стороне этого шестиугольника.
1) `R=2,5`
2) `h=sqrt(6,5^2-2,5^2)=sqrt(42,25-6,25)=6`
Ответ: 6
Номер: 5912F6
Найдите объём многогранника, вершинами которого являются вершины A, C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 7, а боковое ребро равно 9.
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Объем призмы
`V = S_(осн)*h`
1) `V_(призм) = 7*9=63`
2) `V_(ABCB_1) = 1/3*7*9=21`
3) `V_(иск) = 63-21=42`
Ответ: 42
Номер: 805979
Найдите объём многогранника, вершинами которого являются вершины A, C, A1, B1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 9, а боковое ребро равно 4.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
1) `V_(призм)=9*4=36`
2) `V_(ABCB_1)=1/3*9*4=12`
3) `V_(A_1B_1C_1C)=1/3*9*4=12`
4) `V_(иск)=36-12-12=12`
Ответ: 12
Номер: D4DB81
Найдите объём многогранника, вершинами которого являются вершины A1, B1, F1, A правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 15.
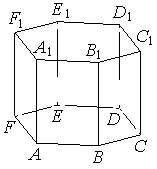
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Площадь части основания правильного шестиугольника, равная отсеченному треугольнику (между любой вершиной и двумя соседними углами), равна 1/6 части от всего основания.
1) `S_(A_1B_1F_1)=1/6*12=2`
2) `V_(иск)=1/3*2*15=10`
Ответ: 10
Номер: 285ADD
Найдите объём многогранника, вершинами которого являются вершины A, C, D, F, A1, C1, D1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11.

Решение:
Площадь части основания правильного шестиугольника, равная прямоугольнику, - между четырьмя вершинами напротив друг друга, равна 2/3 части от всего основания: `S_(ABDE) = 2/3*S`
Объем призмы `V = S_(осн)*h`
1) `S_(ACDF) = 2/3*9=6`
2) `V_(иск) = 6*11=66`
Ответ: 66
Номер: BCD10D
Найдите объём многогранника, вершинами которого являются вершины C, D, E, C1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 14.

Решение:
...
Ответ:
Номер: 077452
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра.
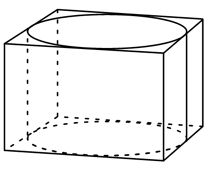
Решение:
Объем прямоугольного параллелепипеда
`V= abh`
`36=6*6*h`
`h=1`
Ответ: 1
Номер: A57713
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.

Решение:
Объем прямоугольного параллелепипеда
`V= abh`
`V=4*4*2=32`
Ответ: 32
Номер: 7BEA25
В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в см.
Решение:
Объем цилиндра
`V = πR^2h`
Диаметр в 2 раза больше, значит радиус также в 2 раза больше.
1) `V_(вод)=πR^2*48`
2) `V_(вод)=π(2R)^2*h`
3) `πR^2*48=4πR^2*h`
`48=4*h`
`h=12`
Ответ: 12
Номер: 0BE824
В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз меньше диаметра первого? Ответ выразите в сантиметрах.
Решение:
Объем цилиндра
`V = πR^2h`
1) `V_(вод)=πR^2*2`
2) `V_(вод)=π(R/5)^2*h`
3) `πR^2*2=(πR)/25*h`
`2=h/25`
`h=50`
Ответ: 50
Номер: BDAC50
В цилиндрическом сосуде уровень жидкости достигает 80 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 6DC4D1
В цилиндрическом сосуде уровень жидкости достигает 405 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 08BD53
В цилиндрическом сосуде уровень жидкости достигает 98 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 32A4DF
В цилиндрическом сосуде уровень жидкости достигает 64 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 6CD9EC
В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 46A627
В цилиндрическом сосуде уровень жидкости достигает 256 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: D03E2C
В цилиндрическом сосуде уровень жидкости достигает 96 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: E2332F
В цилиндрическом сосуде уровень жидкости достигает 20 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 429FD8
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: DA19DC
В цилиндрическом сосуде уровень жидкости достигает 45 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 58515E
В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 48B7A0
В цилиндрическом сосуде уровень жидкости достигает 294 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: F3E5CA
В цилиндрическом сосуде уровень жидкости достигает 192 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 7923C4
В цилиндрическом сосуде уровень жидкости достигает 147 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 9051C6
В цилиндрическом сосуде уровень жидкости достигает 125 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 30D4CA
В цилиндрическом сосуде уровень жидкости достигает 50 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 9493EA
В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз меньше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: BEA763
В цилиндрическом сосуде уровень жидкости достигает 324 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 203E60
В цилиндрическом сосуде уровень жидкости достигает 243 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 90193F
В цилиндрическом сосуде уровень жидкости достигает 320 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 867137
В цилиндрическом сосуде уровень жидкости достигает 6 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз меньше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 9D8E4C
В цилиндрическом сосуде уровень жидкости достигает 5 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 9A6748
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 8CBC41
В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: CFF4F9
В цилиндрическом сосуде уровень жидкости достигает 112 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: CDE9F6
В цилиндрическом сосуде уровень жидкости достигает 216 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: CAB009
В цилиндрическом сосуде уровень жидкости достигает 72 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 602700
В цилиндрическом сосуде уровень жидкости достигает 28 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 1B4376
В цилиндрическом сосуде уровень жидкости достигает 63 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: A0B974
В цилиндрическом сосуде уровень жидкости достигает 384 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: A7F873
В цилиндрическом сосуде уровень жидкости достигает 12 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 06DFB2
В цилиндрическом сосуде уровень жидкости достигает 144 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 0070B6
В цилиндрическом сосуде уровень жидкости достигает 567 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: CD95BE
В цилиндрическом сосуде уровень жидкости достигает 343 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 1D0619
В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
Решение:
...
Ответ:
Номер: 680A1A
В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите угол между прямыми AA1 и BC1.
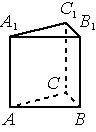
Решение:
1) Искомый угол ∠B1BC1
2) Рассмотрим ΔB1BC1, он прямоугольный и равнобедренный. Тогда углы у основания `(180-90)/2 =45` º
Ответ: 45
Номер: C0F645
В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите расстояние между прямыми AA1 и BC1.
Решение:
...
Ответ:
Номер: 59E06C
В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что BD1=2AD. Найдите угол между диагоналями DB1 и CA1. Ответ дайте в градусах.
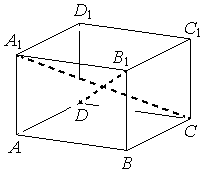
Решение:
Обозначим пересечение диагоналей точкой О
`ΔA_1OB_1` равносторонний, значит
`ΔA_1OB_1=60`º
Ответ: 60
Номер: A629B5
В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что BD1=2AD. Найдите угол между диагоналями DB1 и AC1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: C8B866
В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что DB1=2CB. Найдите угол между диагоналями BD1 и AC1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 9C8BCB
В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что CA1=2A1D1. Найдите угол между диагоналями BD1 и AC1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: F7B88B
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 3, найдите угол между прямыми CD и E1F1. Ответ дайте в градусах.
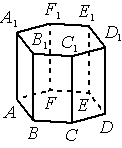
Решение:
Продолжим прямые F1E1 и C1D1 до пересечения в точке K.
1) ∠E1KD - искомый
2)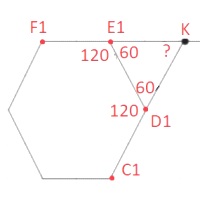
∠KE1D1=180°-120°=60°
∠KD1E1=180°-120°=60° ⇒ ∠E1KD1=180°-2*60°=60°
Ответ: 60
Номер: 257041
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 5, найдите угол между прямыми FA и D1E1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 4C40EE
Дана правильная четырёхугольная призма ABCDA1B1C1D1, площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, A1, B1.
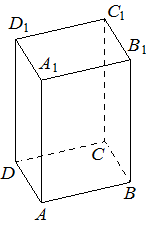
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
1) AB*CB=6
2) `V_(AB B_1A_1C)=1/3*7*AB*CB=1/3*7*6=14`
Ответ: 14
Номер: EFF329
Найдите объём многогранника, вершинами которого являются точки D, A1, B1, C1, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 2.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
`V=1/3*12*2=8`
Ответ: 8
Номер: 362938
Найдите объём многогранника, вершинами которого являются точки D, E, F, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 8, а боковое ребро равно 9.

Решение:
Площадь части основания правильного шестиугольника, равная треугольнику, - между любой вершиной и двумя углами через эту вершину, равна 1/6 части от всего основания: `S_(ABC) = 1/6*S`
Объем призмы `V = S_(осн)*h`
1) `S_(FED)=1/6*8=4/3`
2)`V=4/3*9=12`
Ответ: 12
Номер: 02836B
Найдите объём многогранника, вершинами которого являются точки A, B, C, D, E, F, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 8, а боковое ребро равно 6.

Решение:
...
Ответ:
Номер: 113FBD
Найдите объём многогранника, вершинами которого являются точки B, C, D, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 12.

Решение:
...
Ответ:
Номер: B70519
Найдите объём многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 12.

Решение:
...
Ответ:
Номер: 7E63F8
Найдите объём многогранника, вершинами которого являются точки A, E, F, A1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 13.

Решение:
...
Ответ:
Номер: 15C90E
Найдите объём многогранника, вершинами которого являются точки A, B, C, D, E, F, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 5, а боковое ребро равно 9.

Решение:
...
Ответ:
Номер: AB820F
Найдите объём многогранника, вершинами которого являются точки A, B, F, A1, B1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 8, а боковое ребро равно 15.

Решение:
...
Ответ:
Номер: 9E9C0F
Найдите объём многогранника, вершинами которого являются точки A, B, C, D, E, F, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 3, а боковое ребро равно 9.

Решение:
...
Ответ:
Номер: FD6FA5
Найдите объём многогранника, вершинами которого являются точки F, A1, B1, C1, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4, а боковое ребро равно 3.

Решение:
...
Ответ:
Номер: D4F5A5
Найдите объём многогранника, вершинами которого являются точки A, B, C, D, E, F, B1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 6.

Решение:
...
Ответ:
Номер: 301462
Найдите объём многогранника, вершинами которого являются точки C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 9.

Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
`V_(A_1B_1C_1C) = 1/3*4*9=12`
Ответ: 12
Номер: C6FDB6
Найдите объём многогранника, вершинами которого являются точки A, B, C, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 7, а боковое ребро равно 6.

Решение:
...
Ответ:
Номер: 90C5FB
Найдите объём многогранника, вершинами которого являются точки A, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 9.

Решение:
...
Ответ:
Номер: 010A16
Найдите объём многогранника, вершинами которого являются точки A, B, C, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6, а боковое ребро равно 9.

Решение:
...
Ответ:
Номер: BC715C
Найдите объём многогранника, вершинами которого являются точки A, B, C, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6, а боковое ребро равно 3.

Решение:
...
Ответ:
Номер: 1BC647
Найдите объём многогранника, вершинами которого являются точки B, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 9, а боковое ребро равно 8.

Решение:
...
Ответ:
Номер: F351F0
Найдите объём многогранника, вершинами которого являются точки A, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 2.

Решение:
...
Ответ:
Номер: F007F1
Найдите объём многогранника, вершинами которого являются точки C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 6.

Решение:
...
Ответ:
Номер: EC8EB4
Найдите объём многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 5, а боковое ребро равно 6.

Решение:
...
Ответ:
Номер: 58FE25
Найдите объём многогранника, вершинами которого являются точки B, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 8, а боковое ребро равно 6.

Решение:
...
Ответ:
Номер: 5B4556
Найдите объём многогранника, вершинами которого являются точки A, B, C, B1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6, а боковое ребро равно 3.

Решение:
...
Ответ:
Номер: 67FCAB
Найдите объём многогранника, вершинами которого являются точки A, B, C, B1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 7, а боковое ребро равно 3.

Решение:
...
Ответ:
Номер: E76380
Дана правильная треугольная призма ABCA1B1C1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки A, A1, B1, C1.

Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
`V_(пир A_1B_1C_1A)=1/3*9*4=3*4=12`
Ответ: 12
Номер: FBF62F
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O – центр основания, SO=35, SD=37. Найдите длину отрезка BD.
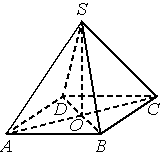
Решение:
ΔSAO
`AO=sqrt(37^2-35^2) = sqrt((37-35)(37+35))=sqrt144=12`
`AC=2*12=24=BD`
Ответ: 24
Номер: C026C8
В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=6, SA=10. Найдите длину отрезка BD.
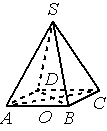
Решение:
...
Ответ:
Номер: B1C644
В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=48, SC=80. Найдите длину отрезка BD.

Решение:
...
Ответ:
Номер: 44F180
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=27, SC=45. Найдите длину отрезка AC.

Решение:
...
Ответ:
Номер: 49E52A
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=48, SC=73. Найдите длину отрезка AC.

Решение:
...
Ответ:
Номер: 703F42
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=18, SD=82. Найдите длину отрезка AC.

Решение:
...
Ответ:
Номер: 0E4DEB
В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=30, SA=34. Найдите длину отрезка AC.

Решение:
...
Ответ:
Номер: 3669AD
В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=14, SD=50. Найдите длину отрезка AC.

Решение:
...
Ответ:
Номер: 80EAE0
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=21, AC=40. Найдите длину отрезка SB.

Решение:
...
Ответ:
Номер: 455F22
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=30, AC=32. Найдите длину отрезка SA.

Решение:
...
Ответ:
Номер: A4BE5E
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=15, AC=40. Найдите длину отрезка SA.

Решение:
...
Ответ:
Номер: D8637E
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=35, BD=24. Найдите длину отрезка SD.

Решение:
...
Ответ:
Номер: CDD528
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=24, AC=20. Найдите длину отрезка SD.

Решение:
...
Ответ:
Номер: ADF7CA
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=28, BD=42. Найдите длину отрезка SC.

Решение:
...
Ответ:
Номер: 636742
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SD=26, AC=20. Найдите длину отрезка SO.

Решение:
...
Ответ:
Номер: 20294D
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SB=29, AC=40. Найдите длину отрезка SO.

Решение:
...
Ответ:
Номер: 1429DE
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SD=37, BD=24. Найдите длину отрезка SO.

Решение:
...
Ответ:
Номер: 12725D
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SD=41, BD=18. Найдите длину отрезка SO.

Решение:
...
Ответ:
Номер: ACAA35
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SA=34, AC=32. Найдите длину отрезка SO.

Решение:
...
Ответ:
Номер: 1AAA8C
В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SC=35, BD=42. Найдите длину отрезка SO.

Решение:
...
Ответ:
Номер: 5BB642
В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.

Решение:
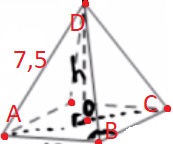
1) ΔABC:
`AC=sqrt(10^2+10^2)=sqrt200=sqrt(100*2)=10sqrt2`
2) ΔACD:
`OD=sqrt((15/2)^2-(5sqrt2)^2) =sqrt(225/4-50/1)=sqrt(25/4)=2,5`
Ответ: 2,5
Номер: 59DC27
В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC равно 37, сторона основания равна 35√2. Найдите объём пирамиды.
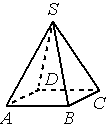
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) ΔABC:
`AC=sqrt((35sqrt2)^2+(35sqrt2)^2)=sqrt(35^2*2+35^2*2)=sqrt(4*35^2)=2*35=70`
2) ΔSOC:
`SO=sqrt(37^2-35^2)=sqrt((37-35)(37+35))=sqrt144=12`
3) `V=1/3(35sqrt2)^2*12=1225*8=9800`
Ответ: 9800
Номер: 0940E2
В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC равно 17, сторона основания равна 15√2. Найдите объём пирамиды.

Решение:
...
Ответ:
Номер: F9348F
Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра.
Решение:
Площадь боковой поверхности
S = 2πRh
1) `S_(бок) = 12π=2πRh`
6=Rh
6=3h
h=2
Ответ: 2
Номер: B29C5A
Площадь боковой поверхности цилиндра равна 24 π, а диаметр основания равен 8. Найдите высоту цилиндра.

Решение:
...
Ответ:
Номер: 9A8020
Площадь боковой поверхности цилиндра равна 20 π, а высота равна 4. Найдите диаметр основания.

Решение:
...
Ответ:
Номер: E85866
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы – прямые).

Решение:
Площадь прямоугольника равна произведению двух сторон.
(6-2)/2=2 размерность неизвестных сторон
Sпов. = 2*4*7+(2*2+6*2)*2+6*4=56+32+24=112
Ответ: 112
Номер: 0CD226
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы — прямые).

Решение:
...
Ответ:
Номер: 1F2997
Диаметр основания конуса равен 40, а длина образующей – 25. Найдите высоту конуса.
Решение:
`25^2=20^2+h^2`
`h^2=225`
`h=15`
Ответ: 15
Номер: 50FCF3
Диаметр основания конуса равен 18, а длина образующей равна 41.

Найдите высоту конуса.
Решение:
...
Ответ:
Номер: 7236F1
Диаметр основания конуса равен 32, а длина образующей равна 65.

Найдите высоту конуса.
Решение:
...
Ответ:
Номер: 6891E2
Диаметр основания конуса равен 10, а длина образующей — 13. Найдите высоту конуса.

Решение:
...
Ответ:
Номер: 66C481
Диаметр основания конуса равен 14, а длина образующей — 25. Найдите высоту конуса.

Решение:
...
Ответ:
Номер: 4C5D0D
Диаметр основания конуса равен 24, а длина образующей — 13. Найдите высоту конуса.

Решение:
...
Ответ:
Номер: 28677C
Высота конуса равна 21, а длина образующей равна 29.

Найдите диаметр основания конуса.
Решение:
...
Ответ:
Номер: 0ABBF1
Высота конуса равна 9, а длина образующей равна 41.

Найдите диаметр основания конуса.
Решение:
...
Ответ:
Номер: 4637FE
Высота конуса равна 24, а длина образующей равна 25. Найдите диаметр основания конуса.

Решение:
...
Ответ:
Номер: FA10DF
Высота конуса равна 5, а длина образующей равна 13. Найдите диаметр основания конуса.

Решение:
...
Ответ:
Номер: 11FDA1
Высота конуса равна 12, а длина образующей равна 13. Найдите диаметр основания конуса.

Решение:
...
Ответ:
Номер: E4EDE4
Высота конуса равна 24, а длина образующей равна 30. Найдите диаметр основания конуса.

Решение:
...
Ответ:
Номер: 6B7BEF
Высота конуса равна 24, а диаметр основания равен 90. Найдите образующую конуса.
Решение:
...
Ответ:
Номер: E29891
Высота конуса равна 24, а диаметр основания равен 20. Найдите длину образующей конуса.

Решение:
...
Ответ:
Номер: AE935B
Высота конуса равна 32, а диаметр основания равен 48. Найдите длину образующей конуса.

Решение:
...
Ответ:
Номер: 013B94
Высота конуса равна 12, а диаметр основания равен 70. Найдите длину образующей конуса.

Решение:
...
Ответ:
Номер: E12074
Высота конуса равна 16, а диаметр основания равен 60. Найдите длину образующей конуса.

Решение:
...
Ответ:
Номер: 944BB0
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса.
Радиус сферы равен 10√2 . Найдите образующую конуса.
Решение:
Пусть A - точка вершины конуса, B - центр основания конуса, C - любая точка по краю основания конуса (получается BC радиус сферы).
Образующая `AC=sqrt((10sqrt2)^2+(10sqrt2)^2)=sqrt(200+200)=20`
Ответ: 20
Номер: F4AA43
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса.

Радиус сферы равен 51√2. Найдите образующую конуса.
Решение:
...
Ответ:
Номер: 280F78
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 26√2. Найдите образующую конуса.

Решение:
...
Ответ:
Номер: 0F93C7
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 23√2. Найдите образующую конуса.

Решение:
...
Ответ:
Номер: CEA269
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 52√2. Найдите образующую конуса.

Решение:
...
Ответ:
Номер: F3318D
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 32√2. Найдите образующую конуса.
Решение:
...
Ответ:
Номер: 0F4E18
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса.

Образующая конуса равна 50√2. Найдите радиус сферы.
Решение:
Пусть A - точка вершины, B - любая точка на поверхности шара и по краю основания конуса и AC - высота конуса, С - центр шара (получается CB радиус).
ΔABC:
`(50sqrt2)^2=R^2+R^2`
`2500*2=2R^2`
`R^2=2500`
`R=50`
Ответ: 50
Номер: 2A5773
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса.

Образующая конуса равна 80√2. Найдите радиус сферы.
Решение:
...
Ответ:
Номер: A4F344
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 11√2. Найдите радиус сферы.

Решение:
...
Ответ:
Номер: 2C6DDC
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 94√2. Найдите радиус сферы.

Решение:
...
Ответ:
Номер: 556A0A
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. undefined Образующая конуса равна 36√2. Найдите радиус сферы.

Решение:
...
Ответ:
Номер: D9F924
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 85√2. Найдите радиус сферы.

Решение:
...
Ответ:
Номер: 0717DF
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 29√2. Найдите радиус сферы.

Решение:
...
Ответ:
Номер: 6C63C7
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=16, A1B1=2, A1D1=8. Найдите длину диагонали AC1.
Решение:
1) ΔABC `AC=sqrt(2^2+8^2) =sqrt68`
2) ΔACC1 `AC_1=sqrt(16^2+sqrt68^2) =sqrt324=18`
Ответ: 18
Номер: D6AA89
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=2, C1D1=6, B1C1=3. Найдите длину диагонали AC1.

Решение:
...
Ответ:
Номер: BD3D53
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=3, AB=6, BC=6. Найдите длину диагонали AC1.
Решение:
...
Ответ:
Номер: 836C43
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=2, A1B1=5, A1D1=14. Найдите длину диагонали CA1.
Решение:
...
Ответ:
Номер: 34CC3D
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=7, CD=6, AD=6. Найдите длину диагонали CA1.

Решение:
...
Ответ:
Номер: 4D5A7F
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=6, CD=17, AD=6. Найдите длину диагонали CA1.

Решение:
...
Ответ:
Номер: 4F57B0
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=6, A1B1=12, A1D1=12. Найдите длину диагонали CA1.

Решение:
...
Ответ:
Номер: 223E12
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=4, AB=8, A1D1=8. Найдите длину диагонали DB1.
Решение:
...
Ответ:
Номер: D95E72
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=12, A1B1=6, AD=4. Найдите длину диагонали DB1.

Решение:
...
Ответ:
Номер: 856E35
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1=7, CD=4, AD=4. Найдите длину диагонали BD1.
Решение:
...
Ответ:
Номер: 5D0145
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=8, CD=8, AD=14. Найдите длину диагонали BD1.

Решение:
...
Ответ:
Номер: BB1641
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=4, AB=2, AD=4. Найдите длину диагонали DB1.

Решение:
...
Ответ:
Номер: 88471E
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=11, AB=2, A1D1=10. Найдите длину диагонали BD1.

Решение:
...
Ответ:
Номер: 9B3521
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AA1=10, AB=5, A1D1=10. Найдите длину диагонали DB1.

Решение:
...
Ответ:
Номер: C296D4
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=9, AB=2, B1C1=6. Найдите длину диагонали BD1.

Решение:
...
Ответ:
Номер: 52BBCD
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AA1=2, CD=1, A1D1=2. Найдите длину диагонали BD1.

Решение:
...
Ответ:
Номер: E170C1
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=9, A1B1=12, A1D1=8. Найдите длину диагонали BD1.

Решение:
...
Ответ:
Номер: 8C61CF
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=4, A1B1=1, BC=8. Найдите длину диагонали DB1.

Решение:
...
Ответ:
Номер: 1495E8
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=4, A1B1=12, A1D1=3. Найдите длину диагонали DB1.

Решение:
...
Ответ:
Номер: 7801FB
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AA1=12, A1B1=12, B1C1=1. Найдите длину диагонали BD1.

Решение:
...
Ответ:
Номер: AC49F5
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=15, AD=8, AA1=21. Найдите площадь сечения, проходящего через вершины B, B1 и D.

Решение:
1) BDD1B1 - сечение
2) ΔABD: `BD=sqrt(15^2+8^2) = sqrt(255+64)=sqrt289=17`
3) `S_(BDD_1B_1) = 21*17=357`
Ответ: 357
Номер: 22DA45
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=21, AD=20, AA1=23. Найдите площадь сечения, проходящего через вершины A, A1 и C.

Решение:
...
Ответ:
Номер: C1FD10
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=3, AD=4, AA1=32. Найдите площадь сечения, проходящего через вершины C, C1 и A.

Решение:
...
Ответ:
Номер: 1B0EDB
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=27, AD=36, AA1=10. Найдите площадь сечения, проходящего через вершины D, D1 и B.

Решение:
...
Ответ:
Номер: EF9136
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C.

Решение:
∠BB1C - искомый
1) ΔBB1C `B_1C=sqrt(12^2+16^2)=sqrt400=20`
2) `sin∠BB_1C = 16/20=0,8`
Ответ: 0,8
Номер: 0628B5
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=9, AD=12, AA1=18. Найдите синус угла между прямыми A1D1 и AC.

Решение:
...
Ответ:
Номер: 15CF1C
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=8, AD=22, AA1=6. Найдите синус угла между прямыми C1D и AB.

Решение:
...
Ответ:
Номер: CA52A9
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=8, AD=6, AA1=21. Найдите синус угла между прямыми A1D1 и AC.

Решение:
...
Ответ:
Номер: 0626A3
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=6, AD=8, AA1=9. Найдите синус угла между прямыми CD и A1C1.

Решение:
...
Ответ:
Номер: 9F08EB
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=9, AD=12, AA1=9. Найдите синус угла между прямыми DD1 и B1C.

Решение:
...
Ответ:
Номер: 913B36
В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.
Решение:
Радиус окружности описанной около равностороннего треугольника.
`R = (sqrt3*a)/3`
`R = 2/3*h`
1) `R=sqrt3*(10,5)/3=3,5sqrt3=(7sqrt3)/2`
2) `h=sqrt(7^2-(7sqrt3/2)^2) = sqrt(49/1-(49*3)/4)=sqrt(49/4)=3,5`
Ответ: 3,5
Номер: 9726B0
В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см.
Решение:
Объем цилиндра
`V = πR^2h`
1)`V_(вод) = 500=πR^2*h`
2)`V_(вод)+V_(дет) = 1,2*500`
`V_(дет) =100`
Ответ: 100
Номер: EBB312
В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. Ответ выразите в куб. см.
Решение:
Объем цилиндра
`V = πR^2h`
1)`V_(вод) = 2800=πR^2*16`
2)`V_(вод)+V_(дет) = πR^2*29`
`2800+V_(дет) = 175*29`
`V_(дет) = 5075-2800=2275`
Ответ: 2275
Номер: 791637
Радиусы двух шаров равны 9 и 12. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Решение:
Площадь поверхности шара:
`S=4πR^2`
1) `S_(пов1)=4π*9^2=324π`
2) `S_(пов2)=4π*12^2=576π`
3) `S_(пов3)=324π+576π=900π`
4) `S_(пов3)=900π=4πR_(нов)^2`
`R_(нов)^2=225`
`R_(нов)=15`
Ответ: 15
Номер: 320DAF
Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 8 раз, а высоту оставить прежней?
Решение:
Объем конуса
`V = 1/3πR^2h`
1)`V_1 = (1/3πR^2h)`
2)`V_2 = 1/3π(8R)^2h=64*(1/3πR^2h)`
в 64 раза
Ответ: 64
Номер: F9E66F
Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 5 раз, а высоту оставить прежней?
Решение:
...
Ответ:
Номер: E1FD6A
Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 6 раз, а высоту оставить прежней?
Решение:
...
Ответ:
Номер: 039CFC
Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 7 раз, а высоту оставить прежней?
Решение:
...
Ответ:
Номер: BA9809
В цилиндрический сосуд, в котором находится 8 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
Решение:
...
Ответ:
Номер: DAB40F
В цилиндрический сосуд, в котором находится 6 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
Решение:
...
Ответ:
Номер: 590166
В цилиндрический сосуд, в котором находится 4 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 2,5 раза. Чему равен объём детали? Ответ выразите в дм3.
Решение:
...
Ответ:
Номер: A25AB8
В цилиндрический сосуд, в котором находится 10 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,6 раза. Чему равен объём детали? Ответ выразите в дм3.
Решение:
...
Ответ:
Номер: 3E171F
В кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и D1C1. Ответ дайте в градусах.

Решение:
D1C1||A1B1
Проведем диагональ A1B. Получим треугольник A1BB1 равнобедренный и прямоугольный.
Угол BA1B1=(180-90)/2=45°.
Ответ: 45
Номер: 0A2A44
В кубе ABCDA1B1C1D1 найдите угол между прямыми CD1 и AD. Ответ дайте в градусах.

Решение:
Найти надо BCD1, так как AD||CB.
Если проведем СD1, то получим прямоугольник A1BСD1. В нем углы равны 90°.
Ответ: 90
Номер: DC1005
В кубе ABCDA1B1C1D1 найдите угол между прямыми AC и BB1. Ответ дайте в градусах.

Решение:
С1С||BB1. Если провести AC1, то получим прямоугольный и равнобедренный треугольник ACC1. Нас интересует искомый прямой угол. То есть угол ACC1 = 90°
Ответ: 90
Номер: 09E9B4
В кубе ABCDA1B1C1D1 найдите угол между прямыми A1D и B1D1. Ответ дайте в градусах.

Решение:
Получается, надо найти угол BDA1.
Если провести диагонали A1D, DB, A1B, то они все равны и получается равносторонний треугольник. А в равностороннем треугольнике углы равны 180/3=60°.
Ответ: 60
Номер: 21B915
В кубе ABCDA1B1C1D1 найдите угол между прямыми AB1 и CD. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: D40EB4
В кубе ABCDA1B1C1D1 найдите угол между прямыми BC1 и A1B1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 1B915A
В кубе ABCDA1B1C1D1 найдите угол между прямыми CB1 и AD. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 55735F
В кубе ABCDA1B1C1D1 найдите угол между прямыми AC и BC1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 2259DC
В кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и AD1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 4C46AC
В кубе ABCDA1B1C1D1 найдите угол между прямыми CB1 и C1D1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: 50D1AB
В кубе ABCDA1B1C1D1 найдите угол между прямыми BD и A1D1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: BCDE6B
В кубе ABCDA1B1C1D1 найдите угол между прямыми CD1 и BC1. Ответ дайте в градусах.

Решение:
...
Ответ:
Номер: D52983
В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение:
Отношение объемов подобных конусов
`V_1/V_2 = k^3`
1) `k=h/(2/3h)=3/2`
2) `V_б/144 = (3/2)^2`
`V_б =(27*144)/8=486`
3) `V_(иск) =486-144=342`
Ответ: 342
Номер: 06254C
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение:
Отношение объемов подобных конусов
`V_1/V_2 = k^3`
`k=2`
1) `V_б/V_м = k^3`
`V_б/25 = 2^3`
`V_б=200`
2) `V_(иск) =200-25=175`
Ответ: 175
Номер: 60E82D
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/3 высоты. Объём жидкости равен 12 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение:
...
Ответ:
Номер: 304821
В сосуде, имеющем форму конуса, уровень жидкости достигает 14 высоты. Объём жидкости равен 1 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение:
...
Ответ:
Номер: DBFAE3
Прямоугольный параллелепипед описан около сферы радиуса 16. Найдите его объём.
Решение:
Объем прямоугольного параллелепипеда
`V=abh`
`V=32^3=(2^5)^3=2^15=2^10*2^5=1024*32=32768`
Ответ: 32768
Номер: 7D0E46
Прямоугольный параллелепипед описан около сферы радиуса 17. Найдите его объём.

Решение:
...
Ответ:
Номер: 202AFE
Прямоугольный параллелепипед описан около сферы радиуса 15,5. Найдите его объём.

Решение:
...
Ответ:
Номер: 3D3E0B
Прямоугольный параллелепипед описан около сферы радиуса 8,5. Найдите его объём.

Решение:
...
Ответ:
Номер: E460C7
Высота цилиндра равна 5, а радиус основания 10. Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
Решение:
...
Ответ:
Номер: 13BCFE
В куб с ребром 3 вписан шар. Найдите объём этого шара, делённый на 𝜋.
Решение:
Объем шара:
`V=4/3*πR^3`
1) `R=3/2`
2) `V=4/3*π(3/2)^3=9/2π=4,5π`
Ответ: 4,5
Номер: 4DADB3
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
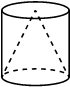
Решение:
Объем конуса:
`V=1/3*πR^2h`
Объем цилиндра
`V=πR^2h`
`V_ц=57*3=171`
Ответ: 171
1)`V_ц=18=πR^2h`
2)`V_k=1/3*πR^2h=1/3*18=6`
Ответ: 6
Номер: 267D7F
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 18.

Решение:
...
Ответ:
Номер: 5272A0
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 48.

Решение:
...
Ответ:
Номер: B43A9D
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 63.

Решение:
...
Ответ:
Номер: AF6921
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 36.

Решение:
...
Ответ:
Номер: BB0BEC
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 45.

Решение:
...
Ответ:
Номер: 96208A
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 162.

Решение:
...
Ответ:
Номер: BEC32B
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 252.

Решение:
...
Ответ:
Номер: BF31A3
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 30.

Решение:
...
Ответ:
Номер: F5558F
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 63.

Решение:
...
Ответ:
Номер: 79DC8F
Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.

Решение:
Площадь поверхности шара:
`S=4πR^2`
Площадь поверхности цилиндра
`S_ш=2πR^2+2πRh`
1) `S_(пов)=48=4πR^2`
`πR^2=12`
2) `S_(полн. пов. ц.)=2πR^2+2πR*2R=6πR^2=6*12=72`
Ответ: 72
Номер: AFD872
Шар вписан в цилиндр. Площадь поверхности шара равна 21. Найдите площадь полной поверхности цилиндра.

Решение:
...
Ответ:
Номер: D039B4
Шар вписан в цилиндр. Площадь поверхности шара равна 29. Найдите площадь полной поверхности цилиндра.

Решение:
...
Ответ:
Номер: 2D1022
Шар вписан в цилиндр. Площадь поверхности шара равна 144. Найдите площадь полной поверхности цилиндра.

Решение:
...
Ответ:
Номер: DEDFDF
Шар вписан в цилиндр. Площадь поверхности шара равна 60. Найдите площадь полной поверхности цилиндра.

Решение:
...
Ответ:
Номер: ED1954
Шар вписан в цилиндр. Площадь поверхности шара равна 120. Найдите площадь полной поверхности цилиндра.

Решение:
...
Ответ:
Номер: AF879C
Цилиндр описан около шара. Объём шара равен 50. Найдите объём цилиндра.

Решение:
Объем шара:
`V=4/3*πR^3`
Объем цилиндра
`V=πR^2h`
1) `V_ш=50=4/3*π*R^3`
`π*R^3=(50*3)/4=75/2`
2) `V_ц=π*R^2*2R=2*πR^3=2*75/2=75`
Ответ: 75
Номер: FCCBC9
Конус вписан в шар (см. рисунок). Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.

Решение:
Объем шара:
`V=4/3*πR^3`
Объем конуса:
`V=1/3*πR^2h`
1) `V_(кон)=47=1/3*πR^2*R`
`πR^2=141`
2) `V_ш=4/3*141=188`
Ответ: 188
Номер: 857802
Конус вписан в шар (см. рисунок). Радиус основания конуса равен радиусу шара. Объём конуса равен 39. Найдите объём шара.

Решение:
...
Ответ:
Номер: B82BDB
Две параллельные плоскости, расстояние между которыми 3, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,91. Найдите радиус шара.
Решение:
...
Ответ:
Номер: 6AB55A
Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите радиус шара.
Решение:
...
Ответ:
Номер: 567C96
Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.
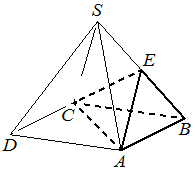
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) `V_(SABCD) = 116=1/3*S_(ABCD)*h`
`S_(ABCD)*h=116*3=348`
2) `V_(EABC) = 1/3 * S_(ABC)*h/2=1/3*1/2*S_(ABCD)*1/2*h=1/12*S_(ABCD)*h=1/12*348=29`
Ответ: 29
Номер: 943A2F
Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
Решение:
Объем цилиндра
`V = πR^2h`
1) `V_1 = πR^2h`
2) `V_2 = π(3R)^2*h/2 = 9/2*πR^2*h`
3) `V_2/V_1=(4,5πR^2*h)/(πR^2*h)=4,5`
Ответ: 4,5
Номер: 4BD794
Объём треугольной пирамиды равен 78. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рисунок). Найдите объём отсечённой треугольной пирамиды.
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Отношение площадей подобных треугольников
`S_1/S_2=k^2`
1) `V_(бол)=1/3*S_(осн. бол.)*h=78` ⇒ `S_(осн. бол.)*h=234`
2) `V_(мал)=1/3*S_(осн. мал.)*h=1/3*1/4*S_(осн. бол.)*h=1/12*234=19,5`
Ответ: 19,5
Номер: 06A191
Площадь боковой поверхности треугольной призмы равна 75. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Решение:
Обозначим стороны маленького треугольника за a b c
1) `S_(бок.пов.бол.) = 2ah+2bh+2ch=2(ah+bh+ch)=75`
2) `S_(бок.пов.мал.) = ah+bh+ch=37,5`
Ответ: 37,5
Номер: 5DADB7
Эти задания устарели. Для короткого ответа сложны, для развернутого структура не соответствует ЕГЭ
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=3:1. Найдите угол между прямыми BE и AC1.
Решение:
...
Ответ:
Номер: 448426
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=1:2. Найдите угол между прямыми BE и AC1.
Решение:
...
Ответ:
Номер: 6B07DE
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=3:2. Найдите угол между прямыми BE и AC1.
Решение:
...
Ответ:
Номер: 1BF9C3
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=2:1. Найдите угол между прямыми BE и AC1.
Решение:
...
Ответ:
Номер: B8FC30
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=2:3. Найдите угол между прямыми BE и AC1.
Решение:
...
Ответ:
Номер: 31824E
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE:EC1=1:3. Найдите угол между прямыми BE и AC1.
Решение:
...
Ответ:
Номер: F4FEF5
Точка E — середина ребра CC1 куба ABCDA1B1C1D1. Найдите угол между прямыми BE и AD.
Решение:
...
Ответ:
Номер: 2B3E5C
Точка E — середина ребра BB1 куба ABCDA1B1C1D1. Найдите угол между прямыми AE и CA1.
Решение:
...
Ответ:
Номер: 063533
Точка E — середина ребра DD1 куба ABCDA1B1C1D1. Найдите угол между прямыми CE и AC1.
Решение:
...
Ответ:
Номер: B6078E
Точка E — середина ребра AA1 куба ABCDA1B1C1D1. Найдите угол между прямыми DE и BD1.
Решение:
...
Ответ:
Номер: F2B2F5
Точка E — середина ребра CC1 куба ABCDA1B1C1D1. Найдите угол между прямыми BE и B1D.
Решение:
...
Ответ:
Номер: 2D40BB
Точка E — середина ребра DD1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью B1CE, если рёбра куба равны 4.
Решение:
...
Ответ:
Номер: E7DFA7
Точка E — середина ребра AA1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью C1DE, если рёбра куба равны 2.
Решение:
...
Ответ:
Номер: CB3D95
Точка E — середина ребра CC1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью A1BE, если рёбра куба равны 2.
Решение:
...
Ответ:
Номер: 613E30
Точка E — середина ребра BB1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью D1AE, если рёбра куба равны 4.
Решение:
...
Ответ:
Номер: E38445
В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые рёбра равны 3, точка D — середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
Решение:
...
Ответ:
Номер: 6E7427
В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые рёбра равны 2, точка D — середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
Решение:
...
Ответ:
Номер: 9255D3
В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые рёбра равны 1, точка D — середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
Решение:
...
Ответ:
Номер: B37053
В правильной треугольной призме ABCA1B1C1 стороны основания равны 3, боковые рёбра равны 2, точка D — середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
Решение:
...
Ответ:
Номер: F807A9
В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые рёбра равны 3, точка D — середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
Решение:
...
Ответ:
Номер: 482999
В правильной треугольной призме ABCA1B1C1 стороны основания равны 3, боковые рёбра равны 1, точка D — середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
Решение:
...
Ответ:
Номер: DA8FEB
В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые рёбра равны 3, точка D – середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
Решение:
...
Ответ:
Номер: 28FCD9
В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые рёбра равны 1, точка D — середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
Решение:
...
Ответ:
Номер: 7CE94E
В правильной треугольной призме ABCA1B1C1 стороны основания равны 3, боковые рёбра равны 2, точка D — середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
Решение:
...
Ответ:
Номер: DB33A0
В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые рёбра равны 2, точка D — середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
Решение:
...
Ответ:
Номер: FEBE6B
В правильной треугольной призме ABCA1B1C1 стороны основания равны 3, боковые рёбра равны 1, точка D — середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
Решение:
...
Ответ:
Номер: EA0937
В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые рёбра равны 3, точка D — середина ребра CC1. Найдите угол между плоскостями ABC и ADB1.
Решение:
...
Ответ:
Номер: C1C474
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые рёбра равны 3. На ребре AA1 отмечена точка E так, что AE:EA1=1:2. Найдите угол между плоскостями ABC и BED1.
Решение:
...
Ответ:
Номер: D13ED8
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые рёбра равны 4. На ребре AA1 отмечена точка E так, что AE:EA1=3:1. Найдите угол между плоскостями ABCи BED1.
Решение:
...
Ответ:
Номер: BCC69B
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые рёбра равны 3. На ребре AA1 отмечена точка E так, что AE:EA1=2:1. Найдите угол между плоскостями ABC и BED1.
Решение:
...
Ответ:
Номер: F91AC0
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 3, а боковые рёбра равны 5. На ребре AA1 отмечена точка E так, что AE:EA1=2:3. Найдите угол между плоскостями ABC и BED1.
Решение:
...
Ответ:
Номер: 70A784
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые рёбра равны 5. На ребре AA1 отмечена точка E так, что AE:EA1=3:2. Найдите угол между плоскостями ABC и BED1.
Решение:
...
Ответ:
Номер: A18F44
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 3, а боковые рёбра равны 4. На ребре AA1 отмечена точка E так, что AE:EA1=1:3. Найдите угол между плоскостями ABC и BED1.
Решение:
...
Ответ:
Номер: 460D1A
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 22, а боковое ребро AA1=7. Точка K принадлежит ребру B1C1 и делит его в отношении 6:5, считая от вершины B1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D и K.
Решение:
...
Ответ:
Номер: 443017
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 10, а боковое ребро AA1=2. Точка O принадлежит ребру A1B1 и делит его в отношении 4:1, считая от вершины A1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и O.
Решение:
...
Ответ:
Номер: AF4793
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 28, а боковое ребро AA1=3. Точка Q принадлежит ребру C1D1 и делит его в отношении 3:4, считая от вершины C1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и Q.
Решение:
...
Ответ:
Номер: FEC4BE
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 20, а боковое ребро AA1=7. Точка M принадлежит ребру A1D1 и делит его в отношении 2:3, считая от вершины D1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D и M.
Решение:
...
Ответ:
Номер: 52A086
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 6, а боковое ребро AA1=1. Точка F принадлежит ребру C1D1 и делит его в отношении 2:1, считая от вершины C1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и F.
Решение:
...
Ответ:
Номер: 59D68D
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 16, а боковое ребро AA1=1. Точка W принадлежит ребру A1B1 и делит его в отношении 1:3, считая от вершины A1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и W.
Решение:
...
Ответ:
Номер: 83088B
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые рёбра равны 3. Точка E — середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
Решение:
...
Ответ:
Номер: 9ED0BC
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые рёбра равны 1. Точка E — середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
Решение:
...
Ответ:
Номер: 4F7460
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, боковые рёбра равны 2. Точка E — середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
Решение:
...
Ответ:
Номер: 1BF133
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые рёбра равны 3. Точка E — середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
Решение:
...
Ответ:
Номер: 133D84
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 3, а боковые рёбра равны 2. Точка E — середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
Решение:
...
Ответ:
Номер: E2E34D
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 3, а боковые рёбра равны 1. Точка E — середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
Решение:
...
Ответ:
Номер: 948CF3
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 3, а боковые рёбра равны 13, найдите расстояние от точки C до прямой A1F1.
Решение:
...
Ответ:
Номер: 5E054E
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E1D1.
Решение:
...
Ответ:
Номер: BF1D67
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 2, найдите расстояние от точки B до прямой A1F1.
Решение:
...
Ответ:
Номер: 8661F8
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найдите расстояние от точки B до плоскости FB1C1.
Решение:
...
Ответ:
Номер: BCE544
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найдите расстояние от точки B до плоскости DEA1.
Решение:
...
Ответ:
Номер: 62C674
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 4, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Решение:
...
Ответ:
Номер: 91D67D
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 12, а боковые рёбра равны 24. Точка G принадлежит ребру MA, причём MG:GA=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B и G параллельно прямой AC.
Решение:
...
Ответ:
Номер: B04B20
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 1, а боковые рёбра равны 2. Точка N принадлежит ребру MC, причём MN:NC=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B и N параллельно прямой AC.
Решение:
...
Ответ:
Номер: ABA54B
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 16. Точка L принадлежит ребру MC, причём ML:LC=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки D и L параллельно прямой AC.
Решение:
...
Ответ:
Номер: D5E2B0
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 15, а боковые рёбра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку D и середину ребра MB параллельно прямой AC.
Решение:
...
Ответ:
Номер: 97799B
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 3, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Решение:
...
Ответ:
Номер: 806993
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно прямой BD.
Решение:
...
Ответ:
Номер: 824C9A
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 18, а боковые рёбра равны 15. Точка R принадлежит ребру MB, причём MR:RB=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки C и R параллельно прямой BD.
Решение:
...
Ответ:
Номер: 580A5F
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 9/2, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно прямой BD.
Решение:
...
Ответ:
Номер: E5F8FE
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 12, а боковые рёбра равны 10. Точка W принадлежит ребру MD, причём MW:WD=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки C и W параллельно прямой BD.
Решение:
...
Ответ:
Номер: FD30C9
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 5. Найдите площадь сечения пирамиды плоскостью, проходящей через точку A и середину ребра MC параллельно прямой BD.
Решение:
...
Ответ:
Номер: 1A48E0
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 32, а боковые рёбра равны 4. Точка K принадлежит ребру MB, причём MK:KB=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки A и K параллельно прямой BD.
Решение:
...
Ответ:
Номер: 205335
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=2, AD=AA1=1. Найдите угол между прямой A1B1 и плоскостью AB1D1.
Решение:
...
Ответ:
Номер: 8A6575
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=2, AD=AA1=1. Найдите угол между прямой AB1 и плоскостью ABC1.
Решение:
...
Ответ:
Номер: B432C2
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=1, AD=AA1=2. Найдите угол между прямой AB1 и плоскостью ABC1.
Решение:
...
Ответ:
Номер: 99B24D
В прямоугольном параллелепипеде ABCDA1B1C1D1 AD=1, AB=AA1=2. Найдите угол между прямой A1D1 и плоскостью AB1D1.
Решение:
...
Ответ:
Номер: DB3648
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=2, AD=AA1=1. Найдите угол между плоскостями CDA1 и CB1D1.
Решение:
...
Ответ:
Номер: D3065C
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=2, AD=AA1=1. Найдите угол между плоскостями ABC1 и AB1D1.
Решение:
...
Ответ:
Номер: 5B7798
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=1, AD=AA1=2. Найдите угол между плоскостями ABC1 и AB1D1.
Решение:
...
Ответ:
Номер: 2C5C87
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=1, AD=AA1=2. Найдите угол между плоскостями CDA1 и CB1D1.
Решение:
...
Ответ:
Номер: F2C8FB
В прямоугольном параллелепипеде ABCDA1B1C1D1 AD=2, AB=AA1=1. Найдите угол между плоскостями ADC1 и DA1C1.
Решение:
...
Ответ:
Номер: 3D75C5
В прямоугольном параллелепипеде ABCDA1B1C1D1 AD=1, AB=AA1=2. Найдите угол между плоскостями ADC1 и DA1C1.
Решение:
...
Ответ:
Номер: 9ED09E
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=4, AD=3, AA1=7. Точка O принадлежит ребру BB1 и делит его в отношении 3:4, считая от вершины B. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки A, O и C1.
Решение:
...
Ответ:
Номер: 6E4F5C
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=5, AD=3, AA1=8. Точка R принадлежит ребру AA1 и делит его в отношении 3:5, считая от вершины A. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки B, R и D1.
Решение:
...
Ответ:
Номер: EE8732
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=4, AD=5, AA1=9. Точка G принадлежит ребру AA1 и делит его в отношении 4:5, считая от вершины A. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки D, G и B1.
Решение:
...
Ответ:
Номер: 2A4B07
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=5, AD=2, AA1=7. Точка M принадлежит ребру CC1 и делит его в отношении 2:5, считая от вершины C. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки D, M и B1.
Решение:
...
Ответ:
Номер: 6A91AA
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=6, AD=4, AA1=10. Точка F принадлежит ребру BB1 и делит его в отношении 2:3, считая от вершины B. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки A, F и C1.
Решение:
...
Ответ:
Номер: BAA560
В правильной треугольной пирамиде MABC с вершиной M высота равна 6, а боковые рёбра равны 9. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон AC и BC параллельно прямой MC.
Решение:
...
Ответ:
Номер: 7F4F51
В правильной треугольной пирамиде MABC с вершиной M высота равна 8, а боковые рёбра равны 17. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон AB и BC параллельно прямой MB.
Решение:
...
Ответ:
Номер: F71EAB
В правильной треугольной пирамиде MABC с вершиной M высота равна 3, а боковые рёбра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон AB и AC параллельно прямой MA.
Решение:
...
Ответ:
Номер: BDB499
В правильной треугольной пирамиде MABC с вершиной M высота равна 9, а боковые рёбра равны 15. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон AB и BC параллельно прямой MB.
Решение:
...
Ответ:
Номер: 2FEF8D
В правильную шестиугольную пирамиду, боковое ребро которой равно 7, а высота равна 3√5, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: F60B4D
В правильную шестиугольную пирамиду, боковое ребро которой равно √5, а высота равна √3, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: E668F4
В правильную шестиугольную пирамиду, боковое ребро которой равно 3√2, а высота равна √10, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: B0895B
В правильную шестиугольную пирамиду, боковое ребро которой равно 2√13, а высота равна 2√10, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: C98CAF
В правильную шестиугольную пирамиду, боковое ребро которой равно √5, а высота равна 1, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: BBBCEC
В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: 9CC43E
В правильную четырёхугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: 884FFB
В правильную четырёхугольную пирамиду, боковое ребро которой равно 3√5, а высота равна 3, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: CCDF4B
В правильную четырёхугольную пирамиду, боковое ребро которой равно 7, а высота равна 3, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: 3F386E
В правильную четырёхугольную пирамиду, боковое ребро которой равно 2√5, а высота равна 4, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: F70136
В правильную четырёхугольную пирамиду, боковое ребро которой равно 2√10, а высота равна 2, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение:
...
Ответ:
Номер: 712D85
Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 6. Найдите расстояние от центра основания конуса до плоскости сечения.
Решение:
...
Ответ:
Номер: BB05B1
Радиус основания конуса равен 9, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 10. Найдите расстояние от центра основания конуса до плоскости сечения.
Решение:
...
Ответ:
Номер: 0D3757
Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4. Найдите расстояние от центра основания конуса до плоскости сечения.
Решение:
...
Ответ:
Номер: E3BE9B
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 8. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.
Решение:
...
Ответ:
Номер: BC9513
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.
Решение:
...
Ответ:
Номер: 9F6B16
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 14. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 9. Найдите площадь сечения большего шара плоскостью α.
Решение:
...
Ответ:
Номер: C52924
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 6. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 4. Найдите площадь сечения большего шара плоскостью α.
Решение:
...
Ответ:
Номер: 3ECCD9

