Все прототипы заданий на применение производной к исследованию функций первой части ЕГЭ по профильной математике

Решение:

Для того чтобы найти наибольшее значение функции, необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=x^3−12x+5$
$y´=3x^2−12$
Теперь найдем значение x при y=0
$0=3x^2−12$
$3x^2=12$
$x^2=4$
$x_1=2$
$x_2=-2$

Исключаем сразу 2, так как это вне отрезка [−3;0], ну и найдем значения для 3 точек x, для экстремума и точек границ отрезка:

$y(-3)=-27+36+5=14$

$y(-2)=-8+24+5=21$

$y(0)=5$

Собственно, как и предполагали, точка x=-2 оказалась экстремумом, причем положительный, то есть максимум, значит там и есть максимальное значение функции.

Ответ: 21

Решение:

Для того чтобы найти наименьшее значение функции, необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=18x^2−x^3+19$
$y´=18*2x−3x^2$
Теперь найдем значение x при y=0
$0=36x−3x^2$ |:3
$0=12x−x^2$
$x(12-x)=0$
$x_1=0$
$x_2=12$

Исключаем сразу 12, так как это вне отрезка, ну и найдем значения для 3 точек x, для экстремума и точек границ отрезка:

$y(-7)=18*49+343+19=1244$

$y(0)=19$

$y(10)=18*100-1000+19=819$

Точка экстремума оказалась точкой минимума, значит она и минимальная на этом отрезке.

Ответ: 19

Решение:

Для того чтобы найти наименьшее значение функции, необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=x^3−x^2−8x+4$
$y´=3x^2−2x-8$
Теперь найдем значение x при y=0
$3x^2−2x-8=0$
$D=4-4*3*(-8)=100=10^2$
$x_1=(2+10)/(2*3)=2$
$x_2=(2-10)/(2*3)=-8/6$ (не подходит, так как вне диапазона отрезка)

Найдем теперь значение функции для 3 точек, для пределов отрезка и точки экстремума

$y(1)=-4$

$y(2)=2^3-2^2-8*2+4=-8$

$y(7)=7^3-49-56+4=343-105+4=242$

Точка экстремума оказалась точкой минимума, значит она и минимальная на этом отрезке.

Ответ: -8

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.

$y=x^3−6x^2+9x+5$
$y´=3x^2−6*2x+9$
$y´=3x^2−12x+9$
Теперь найдем значение x при y=0
$3x^2−12x+9=0$
$D=144-4*3*9=36=6^2$
$x_1=(12+6)/(2*3)=3$
$x_2=(12-6)/(2*3)=1$

Найдем теперь значение функции для 2 точек экстремума

$y(1)=x^3−6x^2+9x+5=1-6+9+5=14$ (макс)

$y(3)=x^3−6x^2+9x+5=27-54+27+5=5$ (мин)

Точка экстремума и точкой максимума оказалась точка где x=1. Сразу скажем, для тех кто не понимает, что это условно локальные точки максимума и минимума, так как у функции есть более значимые по номиналу точки, но они нас не интересуют, так как они не определены. Здесь учащийся по определению должен понимать, что максимум - это локальный максимум.

Ответ: 1

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=x^5+20x^3−65x$
$y´=5x^4+3*20x^2-65$
$y´=5x^4+60x^2-65$ |:5
$y´=x^4+12x^2-13$
$t=x^2$
$y´=t^2−12t-13$
Теперь найдем значение t при y=0
$t^2−12t-13=0$
$D=144-4*1*(-13)=196=14^2$
$t_1=(-12+14)/2=1$
$t_2=(12-14)/2=-13$

тогда $x = sqrt(t)$ для минусовых значений не ищем значения, так как нет смысла ( $x^2>0$ ), а вот для $t_1=1$
$x^2 = 1$
$x_1 = 1$
$x_2 = -1$

Найдем теперь значение функции для точки экстремума в нашем диапазоне [−4;0] и для крайних точек, чтобы определить макс это или мин.

$y(0)=0$

$y(-1)=-1-20+65=44$ (макс)

$y(-4)=-1024-1280+260=-2044$

Точка экстремума и точкой максимума оказалась точка где x=-1.
y(-1)=44

Ответ: 44

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=17+15x−2x^(3/2)$
$y´=15-2*3/2x^(1/2)$
$y´=15-3x^(1/2)$ |:3
$y´=5-x^(1/2)$
$y´=5-sqrtx$
Теперь найдем значение при y´=0
$0=5-sqrtx$
$sqrtx=5$
$x=25$

У нас одна точка экстремума, проверим, что это макс. В принципе, с вероятностью 99 процентов это она, но дабы соблюсти все формальности, докажем, что это все же точка максимума. Возьмем, скажем, значение для x=25, x=16 и x=36 (так легче посчитать, взяли удобные цифры). Можно даже взять и найти значения для производной, по динамике будет понятно что происходит с функцией.

$y´(25)=5-sqrt25=0$

$y´(20)=5-sqrt16=1$

$y´(36)=5-sqrt36=-1$

То есть до 25 функция росла, производная была плюс, потом точка максимум, потом стала убывать. Теперь мы это доказали.

Ответ: 25

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=x^(3/2)−27x+6$
$y´=(3/2)x^(1/2)-27$
$y´=3/2sqrtx-27$
Теперь найдем значение при y´=0
$0=3/2sqrtx-27$
$3/2sqrtx=27$
$x=324$

Точка экстремума входит в наш диапазон отрезка. Необходимо только понять мин это или макс. Возьмем три точки, это пределы отрезка и точку экстремума. Можно даже для производной, чтобы понять динамику функции и сделать заключение по ней.

$y´=3/2sqrtx-27$

$y´(1)=3/2sqrt1-27$ отрицательное значение

$y´(324)=3/2sqrt324-27=0$ точка экстремума, это мы уже вычисляли.

$y´(1)=3/2sqrt422-27$ положительное значение

Собственно получается, что функция убывает до точки экстремума, а потом растет, то есть это точка минимума.

Вычислим значение функции в этой точке.

$y=324^(3/2)−27*324+6 = sqrt324*324-27*324+6=18*324-27*324+6=-2910$

Ответ: -2910

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=1+27x−2xsqrtx$
$y´=27-2*3/2*sqrtx$
$y´=27-3sqrtx$
Теперь найдем значение при y´=0
$3sqrtx=27$
$sqrtx=27/3$
$sqrtx=9$
$x=81$

У нас одна точка экстремума, проверим что это макс. В принципе с вероятностью 99 процентов это она, но дабы соблюсти все формальности докажем, что это все же точка максимума. Возьмем скажем значение для x=64 и x=81 и x=121 (так легче посчитать, взяли удобные цифры). Можно даже взять и найти значения для производной, по динамике будет понятно что происходит с функцией.

$y´ (64)=27-3sqrtx=27-3*8=3$

$y´ (81)=27-3sqrtx=0$

$y´ (121)=27-3sqrtx=27-3*11=-6$

То есть до 81 функция росла, производная была плюс, потом точка максимум, потом стала убывать. Теперь мы это доказали.

Ответ: 81

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=2/3 xsqrtx−6x−5$
$y´=2/3 x^(3/2)−6x−5$
$y´=2/3*3/2 x^(1/2)−6$
$y´=sqrtx-6$
Теперь найдем значение при y´=0
$sqrtx-6=0$
$sqrtx=6$
$x=36$

Нашли точку экстремума, осталось найти минимальное значение. Возьмем пределы отрезка и узнаем в них значения, это сразу нам покажет росла или убывала функция на отрезке, а также минимальное значение, одно из двух.

$y(36)=2/3 *36*6-6*36-5=144-216-5=-77$

$y(9)=2/3*9*3-6*9-5=18-54-5=-41$

Ответ: -77

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=2x+288/x+14$
$y´=2+288*(-1)*1/x^2$
$y´=2-288*1/x^2$

Теперь найдем значение при y´=0
$2-288*1/x^2=0$
$2=288*1/x^2$
$x^2=144$
$x_1=12$
$x_2=-12$ (не берем, так как вне отрезка)

Теперь найдем значение функции в крайних точках отрезка и в точке экстремума, где $x_1=12$

$y(0,5)=2x+288/x+14=1+576+14=591$

$y(12)=2x+288/x+14=24+(144*2)/12+14=62$

$y(25)=2x+288/x+14=50+11,52+14=75,52$

То есть наша точка экстремума является точкой минимума, и это значение нам и надо было найти.

Ответ: 62

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=49/x+x+11$
$y´=-49/x^2+1$
$y´=1-49/x^2$

Теперь найдем значение при y´=0
$1-49/x^2=0$
$1=49/x^2$
$x^2=49$
$x_1=7$
$x_2=-7$ - точки экстремума

Для того чтобы найти точки макс и минимум, необходимо понять, что происходит до и после точки экстремума.

То есть по производной можно взять точки до и после точек экстремума

$y´(-8)=-49/x^2+1$ (будет положительная)

$y´(-5)=-49/x^2+1$ (будет отрицательная)

$y´(8)=-49/x^2+1$ (будет положительная)

Видим, что у нас функция до -7 росла, потом убывала, 0 выколотая точка, потом далее убывает, а далее снова росла.

*Отдельно хотелось бы дать комментарий относительно вычисления точек максимума и минимума для гиперболы, ведь по сути у нас функция гиперболы. Здесь случается парадоксальная ситуация, когда точка локального максимума меньше точки локального минимума. То есть скажем если мы возьмем и подставим значения точек экстремума уже в функцию, чтобы найти значения этой функции то получим:

$y(-7)=49/x+x+11=-7-7+11=-3$

$y(7)=49/x+x+11=7+7+11=25$

И здесь, если не подумать, что это гипербола, можно дать неверный ответ на основании значения функции. А у нас получается, что -3 это максимум в 3 четверти максимум локальный для гиперболы, а 25 это минимум локальный в 1 четверти.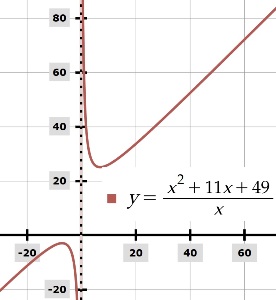

В итоге рекомендация для вычисления точек максимума и минимума использовать именно знаки производной, для гиперболы!

Ответ: -7

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(x+10)^2 x+2$
$y=(x+10)(x+10)x+2$
$y=(x^2+20x+100)x+2$
$y=x^3+20x^2+100x+2$
$y´=3x^2+40x+100$

Теперь найдем значение при y´=0
$0=3x^2+40x+100$
$D=1600-1200=20^2$
$x_1=(-10+20)/6=-20/6$ (не берем, так как не входит в диапазон отрезка)
$x_2=(-10-20)/6=-10$

Находим значение функции в точке x=-10

$y(10)=x^3+20x^2+100x+2=-1000+2000-1000+2=2$

Ну и не помешало бы убедиться, что это максимум, а не минимум.

$y´(-11)=3x^2+40x+100=3*121-440+100$ это больше 0 , значит функция растет

$y´(-9)=3x^2+40x+100=3*81-440+100$ это меньше нуля, значит функция убывает

До - 10 росла, потом убывает, значит действительно x=-10 точка максимума функции, где сама функция равна 2

Ответ: 2

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(x−9)^2 (x+4)−4$
$y=(x−9)(x−9)(x+4)-4$
$y=(x^2-9x-9x+81)(x+4)-4$
$y=(x^2-18x+81)(x+4)-4$
$y=(x^3+4x^2-18x^2-72x+81x+324)-4$
$y=x^3-14x^2+9x+320$

$y´=3x^2-14*2x+9$
Теперь найдем значение при y´=0
$0=3x^2-28x+9$
$D=784-108=676=26^2$
$x_1=(28+26)/6=9$
$x_2=(28-26)/6=1/3$ (не берем, так как не входит в диапазон отрезка)

Находим значение функции в точке x=9 x=7 x=16

$y(7)=x^3-14x^2+9x+320=40$

$y(9)=x^3-14x^2+9x+320=729-1134+81+320=-4$ (точка мин)

$y(16)=x^3-14x^2+9x+320=49*20-4=976$

Ответ: -4

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=(x−4)^2 (x+5)+8$
$y=(x−4)(x−4)(x+5)+8$
$y=(x^2-4x-4x+16)(x+5)+8$
$y=(x^2-8x+16)(x+5)+8$
$y=(x^3+5x^2-8x^2-40x+16x+80)+8$
$y=x^3-3x^2-24x+88$

$y´=3x^2-3*2x-24$
Теперь найдем значение при y´=0
$0=3x^2-6x-24$
$D=36-4*3*(-24)=324=18^2$
$x_1=(6+18)/6=4$
$x_2=(6-18)/6=-2$

По факту мы нашли точки экстремума, так как производная в этих точках равна 0. Но какая из точек максимум, а какая минимум? Теперь на основании знаков производной поймем где функция росла, то есть производная была больше нуля, а где уменьшалась, где производная была меньше 0.

$y´(-3)=3x^2-3*2x-24=3*9+3*2*3-24=27+12-24$ (это больше 0, функция росла)

$y´(0)=3x^2-3*2x-24 = -24$ (меньше 0, функция убывала)

$y´(10)=3x^2-3*2x-24=300-60-24$ (это больше 0, функция росла)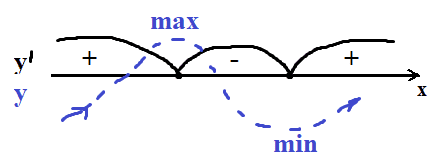

Получается по логике до -2 росла, потом убывала до 4 и потом снова росла. Тогда x = -2 является точкой локального максимума.

Ответ: -2

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=69cosx+71x+48$
$y´=-69sinx+71$

Теперь найдем значение при y´=0
$0=-69sinx+71$
$69sinx=71$
$sinx=71/69$

У нас получается, что нету точки экстремума, так как sinx>1, что не имеет смысла, так как синус не может быть больше 1 или меньше -1.

В итоге без точки экстремума мы значит должны брать границы диапазона заданного нам отрезка, так мы сможем найти значения функции и сравнить их потом, где же больше, где меньше.

$y(0)=69cosx+71x+48=69+48=117$

$y((3π)/2)=69cos((3π)/2)+71((3π)/2)+48$ (будет большое значение из-за 3π/2, где п циклично)

Ответ: 117

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=33x−30sinx+29$
$y´=33−30cosx$

Теперь найдем значение при y´=0
$0=33−30cosx$
$33=30cosx$
$cosx=33/30=1,1$ (не имеет смысла, так как больше 1)

В итоге без точки экстремума мы значит должны брать границы диапазона заданного нам отрезка, так мы сможем найти значения функции и сравнить их потом, где же больше, где меньше.

$y(0)=33x−30sinx+29=33*0-sin0*30+29=29$
$y(-π/2)=(-33π)/2-30sin(π/2)+29$ (будет уходить в минус при бесконечной цикличности п)

Ответ: 29

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=8cosx+30/π x+19$
$y´=-8sinx+30/π$

Теперь найдем значение при y´=0
$0=-8sinx+30/π$
$-8sinx=30/π$
$sinx=30/(8π)=30/(8*3,14)$ (не имеет смысла, так как больше 1)

В итоге без точки экстремума мы значит должны брать границы диапазона заданного нам отрезка, так мы сможем найти значения функции и сравнить их потом, где же больше, где меньше.

$y(0)=8cosx+30/π x+19=8*1+19=27$

$y(-2π/3)=8cosx+30/π x+19=8cos(-(2π)/3)+30/π * (-(2π)/3)+19=-4-20+19=-5$

*в выражении выше $cos(-(2π)/3)=-0,5$ , а во втором слагаемом π сокращается.

Ответ: -5

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=3sqrt2cosx+3x−(3π)/4+7$
$y´=-3sqrt2sinx+3$

Теперь найдем значение при y´=0
$0=-3sqrt2sinx+3$
$3sqrt2sinx=3$
$sqrt2sinx=1$
$sinx=1/sqrt2*sqrt2/sqrt2=sqrt2/2$
$x=π/4$ (это точка экстремума)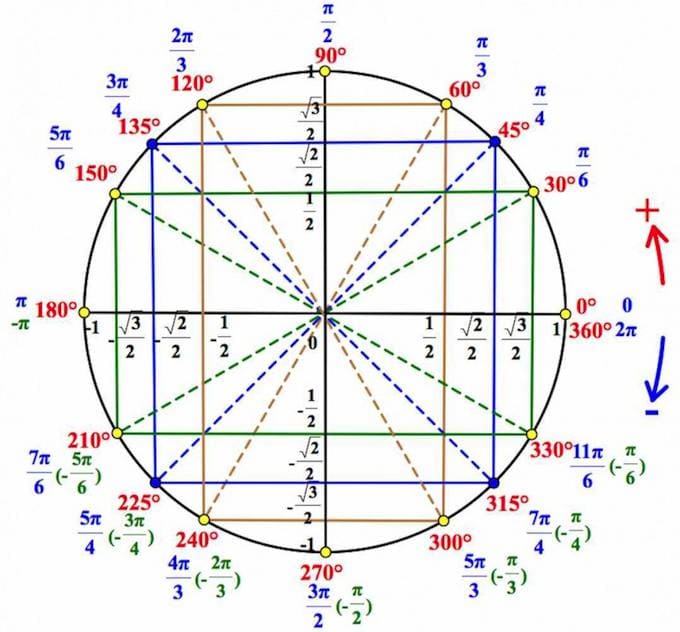

Наш отрезок в 1-й четверти окружности.
Теперь найдем значение для точки экстремума и границ данного нам отрезка, чтобы понять, где же будет наибольшее значение.

$y(π/4)=3sqrt2cos(π/4)+3(π/4)−(3π)/4+7=(3sqrt2sqrt2)/2+7=3+7=10$
$y(0)=3sqrt2cos*0+3*0−(3π)/4+7=$ значение с π не сокращаются, ответ иррациональный
$y(π/2)=3sqrt2cos(π/2)+3(π/2)−(3π)/4+7=$ значение с π не сокращаются, ответ иррациональный

Остается 10

Ответ: 10

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=25x−25tgx+41$
$y´=25-25*1/(cos^2 x)$

Теперь найдем значение при y´=0
$0=25-25*1/(cos^2 x)$
$25=25*1/(cos^2 x)$
$1/(cos^2 x)=1$
$cos^2 x=1$
$cos^2 x=1$
$x=0$

и
$cos^2 x=-1$ не имеет смысла так как это уже x вне нашего диапазона

В итоге находим значения функции для 2 точек, предела отрезка и она же точка экстремума и второго предела отрезка

$y(0)=25x−25tgx+41=25*0-25*tg0+41=41$

$y(π/4)=25x−25tgx+41=25*π/4-25*tgπ/4+41=...$ значение с π не сокращаются, ответ иррациональный

Ответ: 41

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=20tgx−20x+5π−6$
$y´=20*1/(cos^2 x)-20$

Теперь найдем значение при y´=0
$0=20*1/(cos^2 x)-20$
$20*1/(cos^2 x)=20$
$1/(cos^2 x)=1$
$cos^2 x=1$
$cos^2 x=1$
$x=0$

не имеет смысла так как это уже x вне нашего диапазона

В итоге находим значения функции для 3 точек, пределов отрезка и точки экстремума.

$y(0)=20tgx−20x+5π−6=20*tg0-20*0+5π-6=...$ значение с π не сокращаются, ответ иррациональный

$y(-π/4)=20tgx−20x+5π−6=20*tg(-π/4)+20*(π/4)+5π-6=$ значение с π не сокращаются, ответ иррациональный

$y(-π/4)=20tgx−20x+5π−6=20*tg(-π/4)-20*(-π/4)-5π-6=20*1-6=14$
π сокращаются

Ответ: 14

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=e^(2x)−2e^x+8$
$y´=e^(2x)*(2x)´−2e^x$
$y´=2e^(2x)−2e^x$

Теперь найдем значение при y´=0
$0=2e^(2x)−2e^x$
$2e^(2x)=2e^x$
$e^(2x)=e^x$
$e^x(e^x-1)=0$
$e^x=0$ (не имеет решений)
или
$e^x=1$
$x=0$

В итоге ищем значения функция для предела отрезка и для точки экстремума, когда x=0

$y(0)=e^(2x)−2e^x+8=1-2*1+8=7$

$y(-2)=e^(-4)−2e^(-2)+8≈1/(2,7^4)-2/(2,7^2)+8$ первый и второй член будут оч маленькие при вычислении, то есть все равно будет больше 7 при вычитании из 8

$y(1)=e^2−2e+8=1-2*1+8≈7,29-5,4+8$ тоже больше 8

Ответ: 7

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=e^(2x)−4e^x+4$
$y´=e^(2x)*(2x)’−4e^x$
$y´=2e^(2x)−4e^x$ |:2
$y´=e^(2x)−2e^x$

Теперь найдем значение при y´=0
$0=e^(2x)−2e^x$
$e^x(e^x-2)=0$
$e^x=0$ (не имеет решений)
или
$e^x=2$
$x=ln2$

Примерно прикинем диапазон точки экстремума для x.

$e^0=1$
$e^1=2,7$

То есть наше значение x находится где-то между 0 и 1, значит попадает в исследуемый нами отрезок.
Собственно с высокой степенью вероятности наш экстремуму будет нужной нам точкой, но проверим.

Теперь как раз и найдем наименьшее значение функции по трем точкам, $x=ln2$ $x=-1$ $x=2$

$y(-1)=e^(2x)−4e^x+4=...$

$y(2)=e^(2x)−4e^x+4=...$

$y(ln2)=e^(2x)−4e^x+4=e^(2ln2)−4e^(ln2)+4=e^(ln4)−4e^(ln2)+4=4-4*2+4=0$

Собственно берем 0 так как в первых двух уравнениях будет иррациональное решение, в общем кракозябра, которая не подойдет для ответа точно

Ответ: 0

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка минимума - это абсцисса точки, в которой функция достигает минимума.

Итак, найдем производную.
$y=9x−9∙ln(x+3)+4$
$y´=9−9/(x+3)$

Теперь найдем значение при y´=0
$0=9−9/(x+3)$
$9=9/(x+3)$ |:9
$1=1/(x+3)$
$x+3=1$
$x=-2$

Собственно нашли одну точку экстремума. Если это точка максимума, то минимума нет, а значит задание было без смысла, значит это точка минимума.

Хотя проверить не проблема. (-3 выколотая точка, значит попробуем взять что от от выколотой точки до экстремума)

$y´(0)=9−9/(x+3)$ будет положительная производная, значит функция росла

$y´(-2,5)=9−9/(x+3)$ будет отрицательной так как все что будет x+3<1 , будет давать для $9/(x+3)$ значения больше 9.

То есть до точки экстремума было падение, а потом рост функции, значит у нас найдена точкам мин.

Ответ: -2

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=ln(x+9)−10x+7$
$y´=1/(x+9)-10$

Теперь найдем значение при y´=0
$0=1/(x+9)-10$
$1/(x+9)=10$ |:9
$1=10(x+9)$
$10x+90=1$
$x=-8,9$

Собственно нашли одну точку экстремума. Если это точка минимума, то максимума нет, а значит задание было без смысла, значит это все же точка максимума.

Хотя проверить не проблема. (-9 выколотая точка, возьмем где-то между ней и точкой экстремума и вторую с "другой стороны по x" экстремума)

$y´(-8,95)=1/(x+9)-10$ будет положительная, так как все что в знаменателе меньше 0,1. а у нас 0,05 будет давать больше 10, а значит -10 не сможет сделать значение отрицательным

$y´(0)=1/(x+9)-10$ будет отрицательная

То есть до точки экстремума был рост функции, а затем убывание, значит у нас найдена точкам макс.

Ответ: -8,9

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=ln(x+3)^7−7x−9$
$y´=7*1/(x+3)-7$

Теперь найдем значение при y´=0
$0=7*1/(x+3)-7$
$7*1/(x+3)=7$ |:7
$1/(x+3)=1$
$x+3=1$
$x=-2$

Собственно нашли одну точку экстремума. Если это точка минимума, то максимума нет, а значит задание было без смысла, значит это все же точка максимума.

Хотя проверить не проблема. (-3 выколотая точка, возьмем где-то между ней и точкой экстремума и вторую с "другой стороны по x" экстремума)

$y´(-2,5)=7*1/(x+3)-7$ будет положительная, так как все что в знаменателе меньше 1, а у нас 0,5 будет давать больше 1 для дроби, а значит 7*на что-то большее единицы минус 7 будет положительное.

$y´(0)=7*1/(x+3)-7$ будет отрицательная, опять же исходя из логики рассуждения в предыдущем примере

То есть до точки экстремума был рост функции, а затем убывание, значит у нас найдена точкам макс.

Ответ: -2

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=11∙ln(x+4)−11x−5$
$y´=11*1/(x+4)-11$

Теперь найдем значение при y´=0
$0=11*1/(x+4)-11$
$11*1/(x+4)=11$ |:11
$1/(x+4)=1$
$x+4=1$
$x=-3$

Собственно нашли одну точку экстремума. Если это точка минимума, то максимума нет, а значит задание было без смысла, значит это все же точка максимума.

Хотя проверить не проблема. (-4 выколотая точка, возьмем где-то между ней и точкой экстремума и вторую с "другой стороны по x" экстремума)

$y´(-3,5)=11*1/(x+4)-11$ будет положительная, так как все что в знаменателе меньше 1, а у нас 0,5 будет давать больше 1 для дроби, а значит 11*на что-то большее единицы минус 11 будет положительное.

$y´(0)=11*1/(x+4)-11$ будет отрицательная, опять же исходя из логики рассуждения в предыдущем примере

То есть до точки экстремума был рост функции, а затем убывание, значит у нас найдена точкам макс.

Осталось найти значение функции

$y(-3)=11∙ln(-3+4)−11*(-3)−5=11*0+28=28$

Ответ: 28

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=ln(8x)−8x+7$
$y´=1/(8x)*(8x)’-11$
$y´=1/x-8$

Теперь найдем значение при y´=0
$0=1/x-8$
$1/x=8$
$x=1/8$ (входит в наш диапазон)

Собственно нашли одну точку экстремума. Если это точка минимума, то максимума нет, а значит задание было без смысла, значит это все же точка максимума.

Хотя проверим. (0 выколотая. возьмем до точки экстремума и вторую с "другой стороны по x" экстремума)

$y´(1/16)=1/x-8$ будет положительная, так как все что в знаменателе меньше 1/8, а у нас 1/16 будет давать больше 8 для дроби, а значит значение будет положительное.

$y´(5/16)=1/x-8$ будет отрицательная, опять же исходя из логики рассуждения в предыдущем примере выше

То есть до точки экстремума был рост функции, а затем убывание, значит у нас найдена точкам макс.

Осталось найти значение функции

$y(1/8)=ln(8x)−8x+7=ln1-1+7=6$

Ответ: 6

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=ln(x+6)^3−3x$
$y´=3*1/(x+6)-3$

Теперь найдем значение при y´=0
$0=3*1/(x+6)-3$
$3*1/(x+6)=3$ |:3
$x+6=1$
$x=-5$ (входит в наш диапазон)

Собственно нашли точку экстремума. Теперь найдем значения для нее

$y(-5)=ln(x+6)^3−3x=ln1^3+15=0^3+15=15$

Теперь узнаем в пределах отрезка что было с динамикой функции, вычислив знаки производной для этих точек

$y´(-5,5)=3*1/(x+6)-3$ будет положительная, так как все что в знаменателе меньше 1, а у нас 1/2 будет давать больше 3 для дроби, а значит значение будет положительное.

$y´(0)=3*1/(x+6)-3$ будет отрицательная, опять же исходя из логики рассуждения в предыдущем примере выше

То есть до точки экстремума был рост функции, а затем убывание, значит у нас найдена точкам макс.

Ответ: 15

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка минимума - это абсцисса точки, в которой функция достигает минимума.

Итак, найдем производную.
$y=1,5x^2−30x+48∙lnx+4$
$y´=1,5*2x−30+48∙1/x$
$y´=3x−30+48/x$

Теперь найдем значение при y´=0
$0=3x−30+48/x$ |:3
$x−10+16/x=0$
$x(10-x)=1*16$
$-x^2+10x-16=0$
$x^2-10x+16=0$
$D=100-4*16=36$

$x_1=(10+6)/2=8$
$x_1=(10-6)/2=2$

Теперь узнаем в пределах до и после точек экстремума, что было с динамикой функции, вычислив знаки производной для этих точек.

$y´(1)=3x−30+48/x = 3-30+48 = 21$ положительная динамика
$y´(6)=3x−30+48/x= 18-30+8$ отрицательная динамика
$y´(10)=3x−30+48/x = 30-30+4.8$ положительная динамика

Получился слева направо по оси x у нас рост функции до 2, потом падение до 8, потом снова рост. В итоге локальный минимум значит в точке 8

Ответ: 8

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=3x^2−10x+4lnx+11$
$y´=3*2x−10+4*1/x$
$y´=6x−10+4/x$
$y´= (10-6x)/1-4/x$

Теперь найдем значение при y´=0
$0=(10-6x)/1-4/x$
$(10-6x)/1=4/x$
$x(10-6x)/1=4$
$10x-6x^2-4=0$ |:-2
$3x^2-5x+2=0$

$D=25-4*3*2=1$

$x_1=(5+1)/6=1$
$x_2=(5-1)/6=2/3$ (вне диапазона)

Найдем значения для точки x=1

$y(1)=3x^2−10x+4lnx+11=3*1-10*1+4*0+11=4$

Теперь узнаем о поведении функции через производную

$y´(10/11)=6x−10+4/x=(6*10)/11−10+(4*11)/10<0$ функция убывала

$y´(12/11)=6x−10+4/x=(6*12)/11−10+(4*11)/12>0$ функция росла

Значит x = 1 точка локального минимума, а значение функции в ней = 4

Ответ: 4

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=(2x−1)cosx−2sinx+5$
$y´=(2x−1)’cosx−2(x-1)(cosx)’-2cosx$

Теперь найдем значение при y´=0
$2cosx-sinx*(2x-1)-2cosx=0$
$sinx=0$ (не входит в область, так как ноль не включительно в отрезке)
$2x-1=0$
$x=1/2=0,5$

Ответ: 0,5

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка минимума - это абсцисса точки, в которой функция достигает минимума.

Итак, найдем производную.
$y=(x^2−9x+9)*e^(x+27)$
$y´=(x^2−9x+9)´*e^(x+27)+(x^2−9x+9)*(e^(x+27))’$
$y´=(2x-9)*e^(x+27)+(x^2−9x+9)*e^(x+27)$
$y´=e^(x+27)(2x−9+x^2-9x+9)$

Теперь найдем значение при y´=0
$e^(x+27)(2x−9+x^2-9x+9)=0$
$e^(x+27)(2x+x^2-9x)=0$

по множителям
$e^(x+27)=0$ (не имеет решения)
$x^2+2x-9x=0$
$x^2-7x=0$
$x(x-7)=0$
для второго множителя будут корни и они же точки экстремума
$x_1=0$
$x_2=7$

Теперь найдем значение производной, чтобы понять что происходит с функцией.

$y´(-27)=e^(x+27)(x(x-7))=1*(-27*-20)$ будет больше 0

$y´(1)=e^(x+27)(x(x-7))≈3,3*-6$ будет меньше 0

$y´(8)=e^(x+27)(x(x-7))$ первый множитель положительный, второй тоже, значит больше 0

Получается до 0 функция росла, потом убывала, потом с 7 росла. Тогда точка мин x= 7

Ответ: 7

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(3x^2+21x−21)e^x$
$y´=(3x^2+21x−21)’e^x+(3x^2+21x−21)*(e^x)´$
$y´=(3*2x+21)e^x+(3x^2+21x−21)e^x$
$y´=e^x(6x+21+3x^2+21x-21)$

Теперь найдем значение при y´=0
$e^x(6x+21+3x^2+21x-21)=0$

по множителям
$e^x=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$6x+21+3x^2+21x-21=0$
$6x+3x^2+21x=0$
$3x^2+27x=0$ |:3
$x^2+9x=0$
$x(x+9)=0$
$x_1=0$
$x_2=-9$ (не в нашем диапазоне отрезка)

Находим значение производной в точках предела отрезка

$y´(-5)=e^x(x(x+9))=e^x(-5(-5+9))=...$ будет отрицательное значение, так как первый множитель положительный, второй отрицательный

$y´(3)=e^x(x(x+9))=e^x(3(3+9))=...$ будет положительное значение, так как первый множитель положительный, и второй тоже

В итоге понимаем, что тока x=0 это экстремуму минимума, найдем значение функции

$y(0)=(3x^2+21x−21)e^x=-21*1=-21$

Ответ: -21

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=(x−5)^2*e^(x−7)$
$y´=(x^2-10x+25)´*e^(x−7)+(x^2-10x+25)*(e^(x−7))´$
$y´=(2x-10)*e^(x−7)+(x^2-10x+25)*e^(x−7)$
$y´=e^(x−7)*(2x-10+x^2-10x+25)$
$y´=e^(x−7)*(x^2-8x+15)$

Теперь найдем значение при y´=0
$e^(x−7)*(x^2-8x+15)=0$

по множителям
$e^(x−7)=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$x^2-8x+15=0$
$D=64-4*1*15=4=2^2$
$x_1=(8+2)/2=5$
$x_2=(8-2)/2=3$

Нашли точки экстремума функции, осталось определить какая из точек точка максимум

$y´(0)=e^(x−7)*(x^2-8x+15)$ будет положительное значение так как оба множителя будут больше 0

$y´(4)=e^(x−7)*(x^2-8x+15)=e^(x−7)*(16-32+15)$ будет отрицательное значение так как второй множитель меньше 0

$y´(10)=e^(x−7)*(x^2-8x+15)$ будет положительное значение так как оба множителя будут больше 0

Получается до точки 3 функция росла, так как производная положительная, потом с 3 до 5 убывала, потом снова росла. Точка максимума это точка 3

Ответ: 3

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(2x+15)*e^(2x+16)$
$y´=(2x+15)´*e^(2x+16)+(2x+15)*(e^(2x+16))´$
$y´=2*e^(2x+16)+(2x+15)*e^(2x+16)*(2x+16)´$
$y´=2*e^(2x+16)+(2x+15)*e^(2x+16)*2$ |:2
$y´=e^(2x+16)(1+2x+15)$

Теперь найдем значение при y´=0
$e^(2x+16)(1+2x+15)=0$

по множителям
$e^(2x+16)=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$1+2x+15=0$
$2x+16=0$
$x+8=0$
$x=-8$

Найдем значение функции в трех точках. В точке экстремума, которую нашли $x=-8$ и в точках предела данного нам отрезка.

$y(-2)=(2x+15)*e^(2x+16)=(2*-2+15)∙e^(2*-2+16)=11*e^12=...$

$y(-8)=(2x+15)*e^(2x+16)=(2*-8+15)∙e^(2*-8+16)=-1*1=-1$

$y(-12)=(2x+15)*e^(2x+16)=...$

для x = -2 и -12 получаем иррациональные значения, то есть кракозябры, нам точно не подойдет в ФИПИ ответ, поэтому наша точка -1. Собственно можно было найти значение производной, которая показала бы, что в -2 функция убывает, в -12 прибывает, что также указывает на минимальную точку

Ответ: -1

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(x−27)*e^(28−x)$
$y´=(x−27)´*e^(28−x)+(x−27)*(e^(28−x))´$
$y´=1*e^(28−x)+(x-27)*e^(28-x)*(28−x)´$
$y´=e^(28−x)-(x-27)*e^(28-x)$
$y´=e^(28−x)(1-(x-27))$

Теперь найдем значение при y´=0
$e^(28−x)(1-(x-27))=0$

по множителям
$e^(28−x)=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$1-(x-27)=0$
$1-x+27=0$
$x=28$

Найдем значение функции в трех точках. В точке экстремума, которую нашли $x=28$ и в точках предела данного нам отрезка [23;40].

$y(23)=(x−27)*e^(28−x)=...$

$y(28)=(x−27)*e^(28−x)=1*1=1$

$y(40)=(x−27)*e^(28−x)=...$

для x = 23 и 40 получаем иррациональные значения, то есть кракозябры, нам точно не подойдет в ФИПИ ответ, поэтому наша точка 28. Собственно можно было найти значение производной, которая показала бы, что в 23 функция растет, в 40 убывает, что также указывает на максимальную точку, достаточно было бы вычислить значение функции только для x=28, где сама функция равна 1

Ответ: 1

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка минимума - это абсцисса точки, в которой функция достигает минимума.

Итак, найдем производную.
$y=(x^2−17x+17)∙e^(7−x)$
$y´=(x^2−17x+17)’∙e^(7−x)+(x^2−17x+17)(e^(7−x))’$
$y´=(2x-17)*e^(7-x)+(x^2−17x+17)*e^(7−x)*(7−x)’$
$y´=(2x-17)*e^(7-x)-(x^2−17x+17)*e^(7−x)$
$y´=e^(7−x)(2x-17-(x^2−17x+17))$

Теперь найдем значение при y´=0

$e^(7−x)(2x-17-(x^2−17x+17))=0$

по множителям
$e^(7−x)=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$2x-17-(x^2−17x+17)=0$
$-x^2+19x-34=0$ |:-1
$x^2-19x+34=0$
$D=361-4*1*34=225=15^2$
$x_1=(19+15)/2=17$
$x_2=(19-15)/2=2$

Собственно нашли точки экстремума функции, осталось определить где функция росла, где убывала, на основании знака производной.

$y´(0)=e^(7−x)(2x-17-x^2+17x-17)=e^7*(2*0-17-0+17*0-17))=e^7*(-34)=...$ значение будет отрицательное

$y´(10)=e^(7−x)(2x-17-x^2+17x-17)=e^(-3)*(2*10-17-100+170-17)=e^(-3)*56=...$ значение будет положительное

$y´(20)=e^(7−x)(2x-17-x^2+17x-17)=e^(-13)(2*20-17-400+17*20-17)=e^(-13)*(-54)=...$ значение будет отрицательное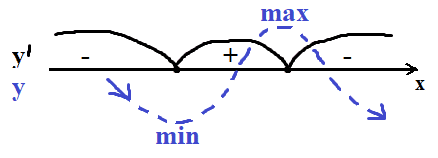

В итоге имеем, до x=2 функция убывала, так как производная отрицательная, потом с 2 до 17 росла, после снова убывала. Значит локальная точка минимума x=2

Ответ: 2

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=(x+5)^2*e^(2−x)$
$y´=(x^2+10x+25)´*e^(2−x)+(x^2+10x+25)*(e^(2−x))´$
$y´=(2x+10)*e^(2−x)+(x^2+10x+25)*e^(2−x)*(2−x)´$
$y´=(2x+10)*e^(2−x)-(x^2+10x+25)*e^(2−x)$
$y´=e^(2−x)(2x+10-(x^2+10x+25))$

Теперь найдем значение при y´=0

$e^(2−x)(2x+10-(x^2+10x+25))=0$

по множителям
$e^(2−x)=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$2x+10-(x^2+10x+25)=0$
$-x^2-8x-15=0$ |:-1
$x^2+8x+15=0$
$D=64-4*1*15=4=2^2$
$x_1=(-8+2)/2=-3$
$x_2=(-8-2)/2=-5$

Собственно нашли точки экстремума функции, осталось определить где функция росла, где убывала, на основании знака производной.

$y´(-10)=e^(2−x)(2x+10-(x^2+10x+25))=e^(2−x)*(2*(-10)+10-(100-100+25))=e^(2−x)*(-20-25+10)=$ значение будет отрицательное

$y´(-4)=e^(2−x)(2x+10-(x^2+10x+25))=e^(2−x)*(2*(-4)+10-(16-40+25))=e^(2−x)*(-8+10-1)=$ значение будет положительное

$y´(0)=e^(2−x)(2x+10-(x^2+10x+25))=e^(2−x)*(0+10-(0+0+25))=$ значение будет отрицательное

В итоге имеем, до x=-5 функция убывала, так как производная отрицательная, потом с -5 до -3 росла, после снова убывала. Значит локальная точка максимума x=-3

Ответ: -3

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(x^2−39x+39)*e^(2−x)$
$y´=(x^2−39x+39)´*e^(2−x)+(x^2−39x+39)*(e^(2−x))´$
$y´=(2x-39)*e^(2−x)-(x^2−39x+39)∙e^(2−x)*(2−x)´$
$y´=(2x-39)*e^(2−x)-(x^2−39x+39)∙e^(2−x)$
$y´=e^(2−x)(2x-39-(x^2-39x+39))$

Теперь найдем значение при y´=0

$e^(2−x)(2x-39-(x^2-39x+39))=0$

по множителям
$e^(2−x)=0$ (не имеет решения)

для второго множителя будут корни и они же точки экстремума
$(2x-39-(x^2-39x+39))=0$
$-x^2+41x-78=0$ |:-1
$x^2-41x+78=0$
$D=1681-4*1*78=1369=37^2$
$x_1=(41+37)/2=39$ (не входит в диапазон нашего отрезка)
$x_2=(41-37)/2=2$

Нашли точки экстремума функции, осталось определить, где функция росла, где убывала, на основании знака производной.

$y´(0)=e^(2−x)(2x-39-(x^2-39x+39))=e^(2−x)(0-39-(0-0+39))$ значение будет отрицательное

$y´(10)=e^(2−x)(2x-39-(x^2-39x+39))=e^(2−x)(200-39-(100-390+39))=e^(2−x)*412$ значение будет положительное

В итоге имеем для нашего отрезка, до x=2 функция убывала, так как производная отрицательная, потом с 2 росла. Значит экстремум $x_2=2$ локальная точка минимума. Найдем значение функции в этой точке.

$y(2)=(x^2−39x+39)∙e^(2−x)=(4−39*2+39)*1=-35$

Ответ: -35

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=−(x^2+36)/x$
$y´=((x^2+36)´(-x)-(x^2+36)(-x)´)/(-x)^2$
$y´=(2x*(-x)-(x^2+36)(-1))/x^2$

Теперь найдем значение при y´=0

$(2x*(-x)-(x^2+36)(-1))/x^2=0$
$(-2x+x^2+36)/x^2=0$
$(-x^2+36)/x^2=0$

по знаменателю
$x≠0$

по числителю
$-x^2+36=0$
$x_1=-6$
$x_2=6$
Нашли точки экстремума, теперь найдем где максимум, где минимум. Возьмем скажем -10, 1, 10

$y´(-10)=(-x^2+36)/x^2=(-100+36)/100=...$ это будет значение со знаком минус
$y´(1)=(-x^2+36)/x^2=(-1+36)/1=...$ это будет значение со знаком плюс
$y´(10)=(-x^2+36)/x^2=(-100+36)/100=...$ это будет значение со знаком минус

Получается у нас до -6 функция убывала, потом до 0 росла, в точке 0 выколотая точка, потом росла, потом опять убывала. Значит Максимум локальный был в точке 6.

Ответ: 6

Решение:

Для того чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
$y=−x/(x^2+225)$
$y´=((−x)´(x^2+225)-(-x)(x^2+225)´)/(x^2+225)^2$
$y´=(-1(x^2+225)+x*2x)/(x^2+225)^2$

Теперь найдем значение при y´=0

$(-x^2-225+2x^2)/(x^2+225)^2=0$
$(x^2-225)/(x^2+225)^2=0$

по знаменателю
$x^2+225≠0$ (нет x удовлетворяющего условию)

по числителю
$x^2-225=0$
$x_1=15$
$x_2=-15$

Нашли точки экстремума, теперь найдем, где максимум и где минимум. Возьмем, скажем, -20, 0, 20. Находим только знаки для числителя, знаменателя и в итоге для значения

$y´(-20)=(x^2-225)/(x^2+225)^2=+/+...$ это будет значение со знаком плюс
$y´(0)=(x^2-225)/(x^2+225)^2=-/+$ это будет значение со знаком минус
$y´(20)=(x^2-225)/(x^2+225)^2=...$ это будет значение со знаком плюс.

Получается у нас до -15 функция росла, потом с -15 до 15 убывала, потом с 15 до бесконечности росла. Значит локальный максимум получился в точке x=-15

Ответ: -15

Решение:

Для того чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=(x^2+441)/x$
$y´=((x^2+441)´x-(x^2+441)x’)/x^2$
$y´=(2x*x-(x^2+441)*1)/x^2$

Теперь найдем значение при y´=0
$(2x*x-(x^2+441)*1)/x^2=0$
$(x^2-441)/x^2=0$
$x^2=441$
$x_1=21$
$x_2=-21$ (вне нашего диапазона отрезка)

Возьмем три точки для нахождения значения функции, это пределы функции и точка экстремума $x_1=21$

$y(2)=(x^2+441)/x=445/2=222,5$

$y(21)=(x^2+441)/x=(441*2)/21=42$

$y(32)=(x^2+441)/x=1465/32≈45,7$

Точка минимума при x = 21, а значение функции 42

Ответ: 42

Решение:

Точка минимума - это абсцисса точки, в которой функция достигает минимума.

1 способ
Мы видимо что у нас под корнем функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

$y=sqrt(x^2+10x+55)$

$x_0=-10/(2*1)=-5$ так как ветви параболы направлены вверх, ведь a > 0, то наша точка вершины является минимальной точкой.

Ответ: -5

2 способ

$y=sqrt(x^2+10x+55)$
$y=sqrt(x^2+10x+25+30)$
$y=sqrt((x+5)^2+30)$

Получается минимально возможное значение функции будет при

$(x+5)^2=0$
$x+5=0$
$x=-5$

Ответ: -5

3 способ
Для того, чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=sqrt(x^2+10x+55)$

$y´=(1(x^2+10x+55)’)/(2sqrt(x^2+10x+55))$
$y´=(2x+10)/(2sqrt(x^2+10x+55))$

Теперь найдем значение при y´=0

$(2x+10)/(2sqrt(x^2+10x+55))=0$

уравнение будет соблюдаться если для числителя выполняется условие
$2x+10=0$
$2x=-10$
$x=-5$

Ответ: -5

Решение:

Точка максимума - это абсцисса точки, в которой функция достигает максимума.

1 способ
Мы видимо что у нас под корнем функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

$y=sqrt(−62−16x−x^2)$

$x_0=16/(2*-1)=-8$ так как ветви параболы направлены вниз, ведь a < 0, то наша точка вершины является точкой максимума.

Ответ: -8

2 способ

$y=sqrt(−62−16x−x^2)$
$y=sqrt(-x^2-16-64+2)$
$y=sqrt(-(x^2-16-64)+2)$
$y=sqrt(2-(x^2-16-64))$
$y=sqrt(2-(x+8)^2)$

Получается максимальное возможное значение функции будет при

$(x+8)^2=0$
$x+8=0$
$x=-8$

Ответ: -8

способ 3

Для того, чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=sqrt(−62−16x−x^2)$

$y´=(1(-62-16x-x^2)’)/(2sqrt(-62-16x-x^2))$
$y´=(-2x-16)/(2sqrt(-62-16x-x^2))$

Теперь найдем значение при y´=0

$(-2x-16)/(2sqrt(-62-16x-x^2))=0$

уравнение будет соблюдаться если для числителя выполняется условие
$-2x-16=0$
$2x=-16$
$x=-8$

Ответ: -8

Решение:

1 способ

Мы видимо что у нас под корнем функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

$y=sqrt(x^2+18x+162)$

$x_0=(-18)/(2*1)=-9$ так как ветви параболы направлены вверх, ведь a > 0, то наша точка вершины является точкой минимума.

$y(-9)=sqrt((-9)^2+18*(-9)+162)=sqrt81=9$

Ответ: 9

2 способ

$y=sqrt(x^2+18x+81+81)$
$y=sqrt((x+9)^2+81)$

Получается, минимальное возможное значение функции будет при

$(x+9)^2=0$
$x+9=0$
$x=-9$

$y(-9)=sqrt((-9)^2+18*(-9)+162)=sqrt81=9$

Ответ: 9

3 способ

Для того, чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=sqrt(x^2+18x+162)$

$y´=(1(x^2+18x+162)´)/(2sqrt(x^2+18x+162))$
$y´=(2x+18)/(2sqrt(x^2+118+162))$

Теперь найдем значение при y´=0

$(2x+18)/(2sqrt(x^2+118+162))=0$

уравнение будет соблюдаться если для числителя выполняется условие
$2x+18=0$
$2x=-18$
$x=-9$
$y(-9)=sqrt((-9)^2+18*(-9)+162)=sqrt81=9$

Ответ: 9

Решение:

1 способ

Мы видимо что у нас под корнем функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

$y=sqrt(−115−28x−x^2)$

$x_0=28/(2*(-1))=-14$

так как ветви параболы направлены вниз, ведь a < 0, то наша точка вершины является точкой максимума. Осталось только найти значение функции в этой точке.

$y(14)=sqrt(−115−28*14−14^2) = sqrt(196-115)=sqrt81=9$

Ответ: 9

2 способ

$y=sqrt(−115−28x−x^2)$
$y=sqrt(81-(x^2+28x+196)$
$y=sqrt(81-(x+14)^2)$

Получается максимально возможное значение функции будет при

$(x+14)^2=0$
$x+14=0$
$x=-14$

Осталось только найти значение функции в этой точке.
$y(14)=sqrt(−115−28*14−14^2) = sqrt(196-115)=sqrt81=9$

Ответ: 9

3 способ

Для того, чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=sqrt(−115−28x−x^2)$

$y´=(1(-115-28x-x^2)’)/(2sqrt(-115-28x-x^2))$
$y´=(-2x-28)/(2sqrt(-115-28x-x^2))$

Теперь найдем значение при y´=0

$(-2x-28)/(2sqrt(-115-28x-x^2))=0$

уравнение будет соблюдаться если для числителя выполняется условие
$-2x-28=0$
$-2x=28$
$x=-14$

Осталось только найти значение функции в этой точке.
$y(14)=sqrt(−115−28*14−14^2) = sqrt(196-115)=sqrt81=9$

Ответ: 9

Решение:

Точка минимума - это абсцисса точки, в которой функция достигает минимума.

1 способ

Мы видимо что у нас в степени функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Минимум будет когда значение x будет в вершине

$x^2+16x+86=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вверх (a>0), то есть найдем точку минимума

$x_0=-16/(2*1)=-8$

Ответ: -8

2 способ
$y=9^(x^2+16x+86)$
$y=9^(x^2+16x+64)+22$
$y=9^((x+8)^2+22)$

Минимальное возможное значение будет при

$(x+8)^2=0$
$x+8=0$
$x=-8$

Ответ: -8

3 способ

Для того, чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=9^(x^2+16x+86)$
$y´=9^(x^2+16x+86)*ln_9 (x^2+16x+86)$

Получается минимальное значение функции будет при
$x^2+16x+86=0$
$2x+16=0$
$x=-8$

Ответ: -8

Решение:

Точка максимума - это абсцисса точки, в которой функция достигает максимума.

1 способ

Мы видимо что у нас в степени функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Максимум будет когда значение x будет в вершине

$−31+14x−x^2=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вниз (a<0), то есть найдем точку максимума.

$x_0=-b/(2a)=-14/(2*(-1))=7$

Ответ: 7

2 способ
$y=9^((-x^2+14x-49)-18)$
$y=9^(18-(x-7)^2)$

Минимальное возможное значение будет при

$(x-7)^2=0$
$x-7=0$
$x=7$

Ответ: 7

3 способ
Для того, чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=9^(−31+14x−x^2)$
$y´=9^(−31+14x−x^2)*ln_9 (-2x+14)$

Получается минимальное значение функции будет при
$-2x+14=0$
$2x=14$
$x=7$

Ответ: 7

Решение:

1 способ

Мы видимо что у нас в степени функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Минимум будет когда значение x будет в вершине

$x^2−12x+38=0$

То есть найдем значение вершины для этой функции - параболы при этом значении. Ветви параболы направлены вверх (a>0), то есть найдем точку минимума.

$x_0=-b/(2a)=12/(2*1)=6$

Осталось только найти значение функции в этой точке.
$y(6)=4^(x^2−12x+38) = 4^(36−12*6+38)=4^2=16$

Ответ: 16

2 способ
$y=4^(x^2−12x+38)$
$y=4^(x^2−12x+36+2)$
$y=4^((x-6)^2+2)$

Минимальное возможное значение будет при

$(x-6)^2=0$
$x-6=0$
$x=6$

Осталось только найти значение функции в этой точке.
$y(6)=4^(x^2−12x+38) = 4^(36−12*6+38)=4^2=16$

Ответ: 16

3 способ
Для того, чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=4^(x^2−12x+38)$

$y´=4^(x^2−12x+38)*ln_4 (x^2-12x+38)’$
$y´=4^(x^2−12x+38)*ln_4 (2x-12)$

Получается минимальное значение функции будет при
$-2x-12=0$
$x=6$

Осталось только найти значение функции в этой точке.
$y(6)=4^(x^2−12x+38) = 4^(36−12*6+38)=4^2=16$

Ответ: 16

Решение:

1 способ

Мы видимо что у нас в степени функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Максимум будет когда значение x будет в вершине

$−4−6x−x^2=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вниз (a<0), то есть найдем точку минимума.

$x_0=-b/(2a)=(-(-6))/(2*(-1))=-3$

Осталось только найти значение функции в этой точке.
$y(-3)=2^(−4−6x−x^2) = 2^(−4−6*2−2^2)=2^5=32$

Ответ: 32

2 способ
$y=2^(−4−6x−x^2)$
$y=2^(5−(x+3)^2)$

Минимальное возможное значение будет при

$(x+3)^2=0$
$x+3=0$
$x=-3$

Осталось только найти значение функции в этой точке.
$y(-3)=2^(−4−6x−x^2) = 2^(−4−6*2−2^2)=2^5=32$

Ответ: 32

3 способ
Для того, чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y(-3)=2^(−4−6x−x^2)$

$y´=2^(-4-6x-x^2)*ln_2 (-4-6x-x^2)’$
$y´=2^(-4-6x-x^2)*ln_2 (-2x-6)$

Получается минимальное значение функции будет при
$-2x-6=0$
$x=-3$

Осталось только найти значение функции в этой точке.
$y(-3)=2^(−4−6x−x^2) = 2^(−4−6*2−2^2)=2^5=32$

Ответ: 32

Решение:

Точка минимума - это абсцисса точки, в которой функция достигает минимума.

1 способ

Мы видимо что у нас в логарифме функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Минимум будет когда значение x будет в вершине, - это возможное минимальное значение

$x^2−30x+249=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вверх (a>0), то есть найдем точку минимума.

$x_0=-b/(2a)=(-(-30))/(2*1))=15$

Ответ: 15

2 способ
$y=log_5 (x^2−30x+249)+8$
$y=log_5 ((x−15)^2+24)+8$

Минимальное возможное значение будет при

$(x−15)^2=0$
$x−15=0$
$x=15$

Ответ: 15

3 способ
Для того, чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=log_5 (x^2−30x+249)+8$

$y´=(1*(x^2-30x+249)’)/((x^2-30x+249)ln5)$
$y´=(2x-30)/((x^2-30x+249)ln5)$

Найдем значение, когда производная равна 0, то есть точку экстремума, она же точка минимума.
$2x-30=0$
$x=15$

Ответ: 15

Решение:

Точка максимума - это абсцисса точки, в которой функция достигает максимума.

1 способ

Мы видимо что у нас в логарифме функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Максимум будет когда значение x будет в вершине, - это возможное максимальное значение

$−40−14x−x^2=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вниз (a<0), то есть найдем точку максимума.

$x_0=-b/(2a)=(-(-14))/(2*(-1))=-7$

Ответ: -7

2 способ
$y=log_8 (-x^2−14x-49+9)+3$
$y=log_5 (9-(x+7)^2)+3$

Минимальное возможное значение будет при

$(x+7)^2=0$
$x+7=0$
$x=-7$

Ответ: -7

3 способ
Для того, чтобы найти наибольшее значение функции, необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=log_8 (−40−14x−x^2)+3$

$y´=(1*(−40−14x−x^2)´)/((-40-14x-x^2)ln8)$
$y´=(-2x-14)/((-40-14x-x^2)ln8)$

Найдем значение, когда производная равна 0, то есть точку экстремума, она же точка максимума.
$-2x-14=0$
$x=-7$

Ответ: -7

Решение:

1 способ
Мы видимо что у нас в логарифме функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Минимум будет когда значение x будет в вершине, - это возможное минимальное значение

$−40−14x−x^2=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вверх (a>0), то есть найдем точку минимума.

$x_0=-b/(2a)=(-14)/(2*1)=-7$

Точку экстремума минимум нашли, теперь найдем значение функции в ней.
$y(-7)=log_4 (x^2+14x+305)+9=log_4 (49-98+305)+9=log_4 256+9=4+9=13$

Ответ: 13

2 способ
$y=log_4 (x^2+14x+305)+9$
$y=log_4 ((x+7)^2+256)+9$

Минимальное возможное значение будет при

$(x+7)^2=0$
$x+7=0$
$x=-7$

Точку экстремума минимум нашли, теперь найдем значение функции в ней.
$y(-7)=log_4 (x^2+14x+305)+9=log_4 (49-98+305)+9=log_4 256+9=4+9=13$

Ответ: 13

3 способ
Для того, чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.
$y=log_4 (x^2+14x+305)+9$

$y´=(1*(x^2+14x+305)’)/((x^2+14x+305)ln4)$
$y´=(2x-14)/((x^2+14x+305)ln4)$

Из числителя

$(2x+14)=0$
$2x=-14$
$x=-14/2=-7$

Точку экстремума минимум нашли, теперь найдем значение функции в ней.
$y(-7)=log_4 (x^2+14x+305)+9=log_4 (49-98+305)+9=log_4 256+9=4+9=13$

Ответ: 13

Решение:

1 способ
Мы видимо что у нас в логарифме функция параболы, где вершина находится по уравнению.

$x_0=-b/(2a)$

Максимум будет когда значение x будет в вершине, - это возможное максимальное значение

$4−4x−x^2=0$

То есть найдем значение вершины для этой функции - параболы. Ветви параболы направлены вниз (a<0), то есть найдем точку максимума.

$x_0=-b/(2a)=(4)/(2*-1)=-2$

Точку экстремума минимум нашли, теперь найдем значение функции в ней.
$y(-2)=log_8 (4−4x−x^2)+8=log_8 (4−4*(-2)−(-2)^2)+8=1+8=9$

Ответ: 9

2 способ
$y=log_8 (4−4x−x^2)+8$

$y=log_8 (8−(x+2)^2)+8$

Максимальное возможное значение будет при

$(x+2)^2=0$
$x+2=0$
$x=-2$

Точку экстремума минимум нашли, теперь найдем значение функции в ней.
$y(-2)=log_8 (4−4x−x^2)+8=log_8 (4−4*(-2)−(-2)^2)+8=1+8=9$

Ответ: 9

3 способ
Для того, чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0, это точка экстремума функции (мин или макс).

Итак, найдем производную.

$y=log_8 (4−4x−x^2)+8$

$y´=(1*(4-4x-x^2)’)/((4-4x-x^2)ln8)$
$y´=(-2x-4)/((4-4x-x^2)ln8)$

Из числителя

$(-2x-4)=0$
$-2x=4$
$x=-2$

Точку экстремума минимум нашли, теперь найдем значение функции в ней.

$y(-2)=log_8 (4−4x−x^2)+8=log_8 (4−4*(-2)−(-2)^2)+8=1+8=9$

Ответ: 9

Все прототипы заданий на применение производной к исследованию функций первой части ЕГЭ по профильной математике

Степенные

Тригонометрические

Показательные

Логарифмические

Произведения

Частные

Без помощи производной