Что надо знать для решение задач - функций. (кратко)
Для прямой
`y=kx+b`
b отвечает за смещение по оси y, это координата пересечения оси y.
k - отношение возрастания y к x, то есть по факту тангенс прямоугольного треугольника, где вершины на прямой, а угол 90 градусов достраивается из вершин (отвечает за наклон прямой `k=tgα`)
`k=y/x` y,x - номиналы сторон прямоугольного треугольника.
Для параболы (квадратичной функции)
`y=ax^2+bx+c`
a - если ветвь возрастает квадратично, то есть `y=x^2`, то a = 1 (смотрим от вершины).
Если зависимость другая, то надо брать точки на параболе и вычислять значение с помощью системы уравнений.
Коэффициент с всегда равен координате пересечения параболы с осью Оy: c = 2
Координата х вершины параболы находится по формуле:
`x=(-b)/(2a)`
Для логарифма
(для нахождения b) Логарифмическая функция сама по себе проходит всегда через току (1;0), так как при `log_2 x` или `log_3 x` и т.д. при y = 0, x должен быть равен 1, так как любое число в нулевой степени будет давать 1.
Для гиперболы
Симметричная относительно 0;0.
Для косинуса, синуса
Функция косинуса сама по себе без каких-либо коэффициентов проходит осью симметрии через x=0, то есть ее верх и низ по сути симметричен. Смещение вверх или вниз посредством коэффициента.
Все прототипы заданий из первой части ЕГЭ по профильной математике, в которых нужно найти значения по графику функции (по рисунку).
Прямая
На рисунке изображён график функции вида f(x)=kx+b. Найдите значение f(7).
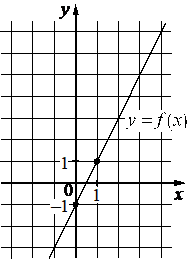
Решение:
1 способ
Имеем смещение по оси абсцисс вправо 1, а по оси ординат 2 вверх.
k отвечает за наклон прямой и `k=tgα`, b - координата пересечения оси y.
`k=tgα=2/1=2`
`b=-1`
`y=2x-1`
`f(7)=2*7-1=13`
2 способ
Он основан как раз на утверждении , - имеем смещение по оси абсцисс вправо 1, а по оси ординат 2 вверх.
Причем у нас 1 шаг уже на x=1, а нам надо 7 шагов, то есть остается 6 шагов по оси x, до x=7, это 6*2=12 шагов вверх по оси, да 1 по y уже был после первого шага. итого 12+1=13
Ответ: 13
# Номер: 9CC815
На рисунке изображён график функции f(x) = kx + b. Найдите значение x, при котором f(x) = —13,5.
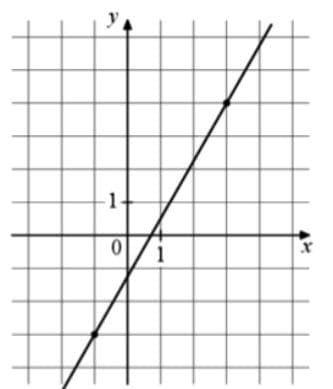
Решение:
Достроим прямоугольный треугольник по выделенным точкам
`k=tgα=7/4`
`y=7/4x+b`
Возьмем точку (3;4) и подставим значения от нее в функцию, чтобы найти b
`4=7/4*3+b`
`b=4/1-21/4=-5/4`
В итоге получаем
`y=7/4x-5/4`
`-13,5=7/4x-5/4` |:4
`-54=7x-5`
`-49=7x`
`x=-7`
Ответ: -7
Номер: mathege
Парабола
На рисунке изображён график функции вида `f(x)=ax^2 + bx + с`. Найдите значение f(— 2).
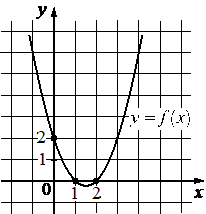
Решение:
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
c = 2
Ветви параболы направленны вверх, коэффициент а положительный. По вершине и ещё одной точке, заметим, что при возрастании координаты х на 2,5, координата у вырастает на 6,25, т.к. `2,5^2 = 6,25`, значит это обычная парабола с а = +1:
а = +1
Координата х вершины параболы (х = 1,5) находится по формуле:
`x=(-b)/(2a)`
Подставим известные значения и найдём b:
`1,5=(-b)/2`
`-b=1,5*2=3`
`b = –3`
Функция имеет вид:
`f(x) = +1x^2 – 3x + 2`
Найдём f(–2):
`f(–2) = +1*(–2)^2 – 3*(–2) + 2 = 4 + 6 + 2 = 12`
Ответ: 12
Номер: BC2802
На рисунке изображён график функции `f(x)=ax^2 + bx + с`, где числа а, b и с — целые. Найдите f(2).
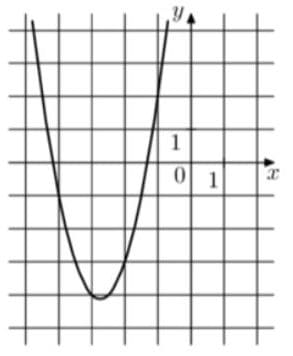
Решение:
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
(на графике его нет)
Ветви параболы направленны вверх, коэффициент а положительный. По вершине и ещё одной точке заметим, что при возрастании координаты х на 1, координата у вырастает на 5, т.к. зависимость не просто квадратичная, а с коэффициентом больше 1, - но какой!?
Координата х вершины параболы находится по формуле:
`x=(-b)/(2a)`
(нет известных данных для вычисления)
Ни один из методов анализа не подходит, значит будем составлять систему уравнений по графику.
Возьмем точки (-4;-1) (-3;-4) (-1;2)
1)
`{(2=(1-)^2*a-b+c),(-1=(-4)^2*a-4b+c),(-4=(-3)^2*a-3b+c):}`
Из верхнего и среднего
`3=-15a+3b`
Из среднего и нижнего
`-3=-7a+b`
Составим из этих заключений новую систему
`{(3=-15a+3b),(-3=-7a+b):}`
Умножим части нижнего уравнения на -3
`{(3=-15a+3b),(9=21a-3b):}`
складываем одно уравнение с другой, по частям, левую с левой, правую с правой, чтобы исключить b, получаем
`3+9=21a-15+3b-3b`
`12=6a`
`a=2`
`-3=-7a+b`
`-3=-7*2+b`
`b=-3+14=11`
`2=1*2-11+c`
`c=11`
`y=2x^2+11x+11`
2)
теперь найдем значение функции для 2
`f(2)=2*2^2+11^2+11=41`
Ответ: 41
Номер: mathege
На рисунке изображён график функции `f(x)=ax^2 + bx + с`, где числа а, b и с — целые. Найдите f(−12).
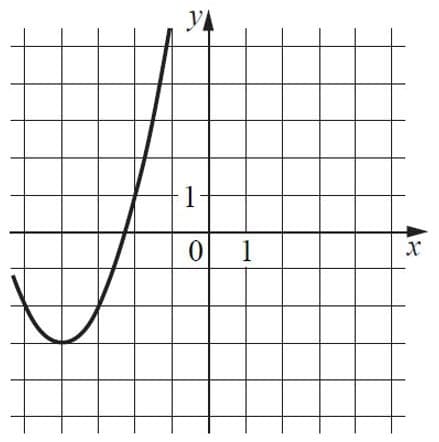
Решение:
Ветви параболы направленны вверх, коэффициент а положительный. По вершине и ещё одной точке заметим, что при возрастании координаты х на 2, координата у вырастает на 4, т.к. зависимость квадратичная, а = 1, так как `2^2=4`
Теперь найдем вершину параболы.
Координата х вершины параболы находится по формуле:
`x=(-b)/(2a)`
х=-4,
`-4=(-b)/(2*1)`
`-b=-8`
`b=8`
В итоге получаем функцию:
`y=1*x^2+8x+c`
Если взять значения из точки (-2;1) и подставить в нее, то можно как раз узнать с
`y=1*x^2+8x+c`
`1=1*(-2)^2+8*-2+c`
`1=4-16+c`
`с=13`
получаем функцию:
`y=1*x^2+8x+13`
Теперь осталось подставить -12 вместо x, то есть x = -12 и произвести вычисления.
f(12)=144-96+13=61
Ответ: 61
Номер: Демоверсия 2022
На рисунке изображён график функции `f(x) = —2х^2 + bx + с`. Найдите f(5).
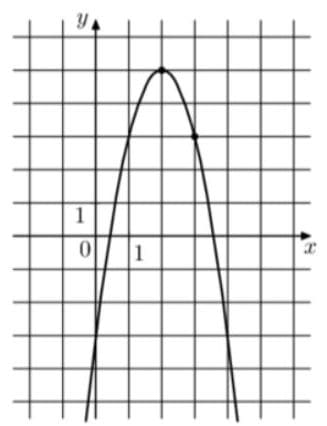
Решение:
Сразу видим, что a = -2 в квадратичной функции.
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
(на графике с=-3)
Значение b можно узнать если взять номиналы из точки (3;3)
`f(x) = -2х^2 + bx - 3`
`3 = -2*3^2 + 3b - 3`
`3 = -18 + 3b - 3`
`3b = 18+3+3`
`b=8`
Получаем функцию:
`f(x) = —2х^2 + 8x -3`
Тогда
`y = —2х^2 + 8x -3`
`y = —2*5^2 + 8*5 -3`
`y = -50+40-3 = -13`
Ответ: -13
Номер: mathege
На рисунке изображён график функции `f(x) = 2х^2 + bx + с`. Найдите f(—5).
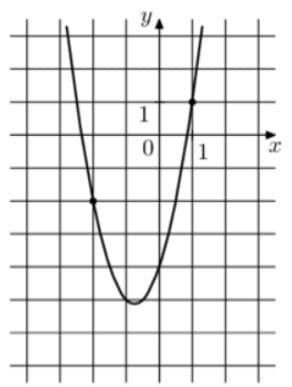
Решение:
Сразу видим, что a = 2 в квадратичной функции.
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
(на графике с=-4)
Значение b можно узнать, если взять номиналы из точки (-2;-2)
`f(x) = 2х^2 + bx + с`
`-2 = 2*(-2)^2 -2*b - 4`
`-2 = 2*4 -2*b - 4`
`-2 = 4 - 2*b`
`2*b = 4 + 2`
`b = 6/2=3`
Собственно, получаем функцию
`f(x) = 2х^2 + 3x -4`
для нее и находим f(—5)
`y = 2*(-5)^2 + 3*(-5) - 4`
`y = 50 - 15 - 4 = 31`
Ответ: 31
Номер: mathege
На рисунке изображён график функции `f(x) = ax^2 — 4х + с`. Найдите f(—3).
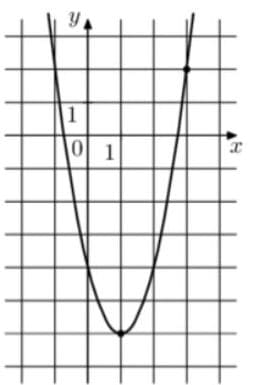
Решение:
Из функции сразу видно что коэффициент b = -4
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
(на графике с=-4)
Координата х вершины параболы находится по формуле:
`x=(-b)/(2a)` При этом из графика видно, что вершина имеет координаты (1;-6) x = 1. Найдем a.
`1=-(-4)/(2a)`
`2a=4`
`a=2`
Собственно, все коэффициенты найдены, получаем
`f(x) = ax^2 — 4х + с`
`f(-3)= 2x^2 — 4х - 4`
`y = 2*3^2 - 4*-3 - 4`
`y = 18 - 4*3 - 4 = 26`
Ответ: 26
Номер: mathege
На рисунке изображён график функции `f(x) = ax^2 — 3x + с`. Найдите f(—4).
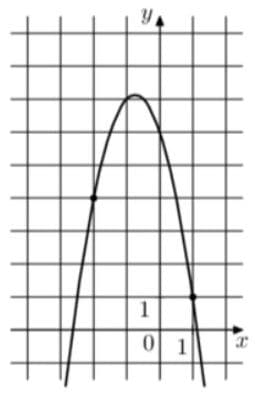
Решение:
Из функции сразу видно что коэффициент b = -3.
Коэффициент с всегда равен координате пересечения параболы с осью Оy:
(на графике с=6)
Из координат точки (-2;4) и функции `f(x) = ax^2 — 3x + 6` можно найти a
`f(x) = ax^2 — 3x + 6`
`4 = a*-2^2 — 3*-2 + 6`
`4 = a*4 + 6 + 6`
`-4a = 12-4=8`
`a = -2`
Собственно, все коэффициенты найдены, получаем
`f(x) = 2x^2 — 3x + 6`
`f(-4) = 2x^2 — 3x + 6`
`y = -2*-4^2 — 3*-4 + 6`
`y = -2*16 + 12 + 6`
`y = -32 + 18 = -14`
Ответ: -14
Номер: mathege
На рисунке изображён график функции `f(x) = ax^2 + bx — 3`. Найдите f(8).
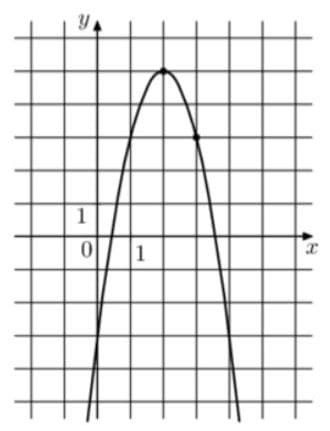
Решение:
Из функции сразу видно, что коэффициент с = -3.
При этом мы видим, что для левой ветки возрастание х на 2 дает прирост 8, значит получается минифункция
`-ax^2=у`
`-a*2^2=8`
`-a*4=8`
`-a=2`
`a=-2`
* минус здесь появился из-за того, что ветви функции направлены вниз, значит a меньше 0
вот из нее и получаем значение a
Теперь из вершины функции, которая вычисляется по формуле
`x=(-b)/(2a)` и по координатам (2;5) x = 2 получаем
`x=(-b)/(2a)`
`2=(-b)/(2*-2)`
`2=(-b)/(-4)`
`-b=-8`
`b=8`
В итоге есть все коэффициенты, находим f(8)
`f(8) = ax^2 + bx — 3`
`f(8) = -2x^2 + 8x — 3`
`y = -2*8^2 + 8*8 — 3`
`y = -128 + 64 - 3`
`y = -128 + 64 - 3`
`y = -67`
Ответ: -67
Номер: mathege
На рисунке изображён график функции `f(x) = ax^2 + bx — 6`. Найдите f(—6).
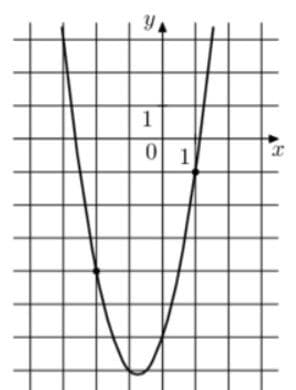
Решение:
Из функции сразу видно что коэффициент с = -6.
Коэффициент а по графику найти трудно, так как нет точной точки вершины и растет он не просто квадратично, а все же имеет какое-то значение а.
Здесь можно составить систему уравнений по точкам:
1)
(1; -1)
(-2; -4)
Подставляем значения координат в функцию x и y
`{(-1=a+b-6 |*2),(-4=4a-2b-6):}`
`{(-2=2a+2b-12),(-4=4a-2b-6):}`
`-6=6a-18`
`12=6a`
`a=2`
`-1-2+6=b`
`b=3`
2)
`y=2x^2+3x-6`
`f(-6)=2*(-6)^2+3(-6)-6=48`
Ответ: 48
Номер: mathege
Гипербола
На рисунке изображён график функции вида `f(x) = k/x`. Найдите значение f(10).
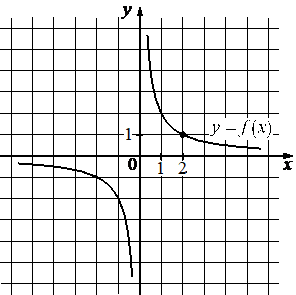
Решение:
Возьмём точку, принадлежащую гиперболе (2; 1) и подставим в функцию, найдём k.
`1=k/2`
`k = 1·2 = 2`
Функция имеет вид:
`f(x)=2/x`
Найдём f(10):
`f(10)=2/10=0,2`
Ответ: 0,2
Номер: 08C3D9
На рисунке изображён график функции вида `f(x) = k/x`. Найдите значение f(10).

Решение:
Возьмём точку, принадлежащую гиперболе (-1; 1) и подставим в функцию, найдём k.
`-1=k/1`
`k = -1 * 1 = -1`
Функция имеет вид:
`f(x)=-1/x`
Найдём f(10):
`f(10)=-1/10=-0,1`
Ответ: -0,1
Номер: 06DEEE
На рисунке изображён график функции вида `f(x) = k/x +a`. Найдите f(—12).
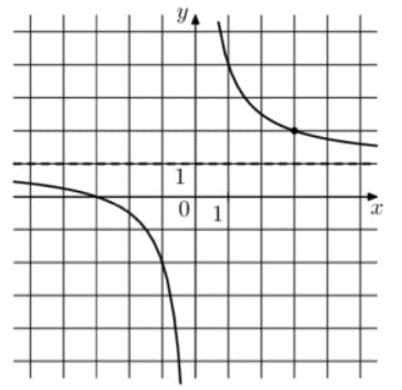
Решение:
1) a = 1 так как гипербола выше "обычной" на 1 (предел, к которому стремится гипербола, изображен штриховой линией на графике)
`y=k/x+1`
2) (3;2)
`2=x/3+1`
`k/3=1`;
`k=3`;
`y=3/x+1`
3)
`f(-12) = 3/(-12)+1=1-1/4=3/4=0,75`
Ответ: 0,75
Номер: mathege
На рисунке изображён график функции `f(x) = k/x +a`. Найдите, при каком значении x значение функции равно 2,2.
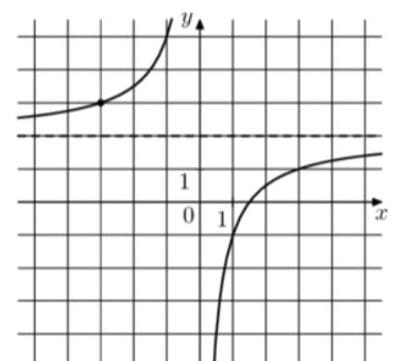
Решение:
1) a = 2 так как гипербола выше "обычной" на 2 (предел к которому стремится гипербола изображен штриховой линией на графике)
`f(x) = k/x +2`
2) Из координат известной точки (-3;3) можно подставив значения в функцию найти k
`3=k/(-3)+2`
`1=k/(-3)`
`k=-3`
Получаем
`f(x) = (-3)/x +2`
3) Находим интересующее нас значение x
`2,2=(-3)/x +2`
`0,2=(-3)/x`
`x=(-3*0,5)/(0,2*5)=-15/1=-15`
Ответ: -15
Номер: mathege
На рисунке изображён график функции `f(x) = k/(x+a)`. Найдите f(19).
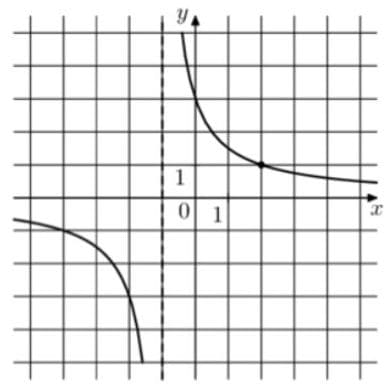
Решение:
1) a=1 так как гипербола смещена относительно y на 1 деление.
`y=k/(x+1)`
2) `1=k/(2+1)`, k = 3
`y=3/(x+1)`
3) `f(19)=3/(19+1)=(3*5)/(20*5)=15/100=0,15`
Ответ: 0,15
Номер: mathege
На рисунке изображён график функции вида `f(x) = k/(x +a)`. Найдите значение X, при котором f(x) = —0,04.
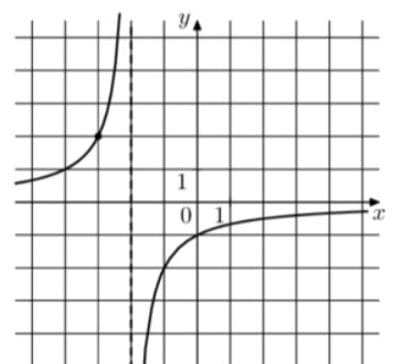
Решение:
1) a=2 так как гипербола смещена относительно y на 2 деления.
`y=k/(x+2)`
2) (-3; 2)
`2=k/(-3+2)`
`k=2*(-1)=-2`
`y=-2/(x+2)`
3)
`-0,04=(-2)/(x+2)`
`x+2=(-2)/(-0,04)`
`x+2=50`
`x=48`
Ответ: 48
Номер: mathege
На рисунке изображён график функции `f(x) = (kx+a)/(x +b)`. Найдите a.
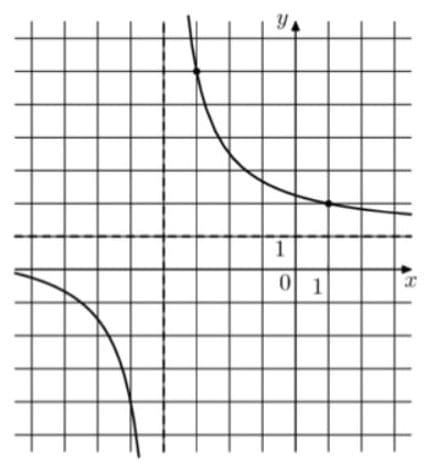
Решение:
1) b=4 так как гипербола смещена относительно y на 4 деления.
К положительная так как располагается в 1 и 3 четверти.
k=5 так как функция проходит через точки в смещенной системе координат (штриховая линия) (1;5) и (5;1).
Кроме того, добавим 1, так как штриховая система смещена относительно реальной вверх на 1.
`y=5/(x+4)+1`
Приведем к общему знаменателю
`y=(5+x+4)/(x+4)=(1x+9)/(x+4)`
Собственно, сопоставляя информацию в условии и получившемся уравнении, нетрудно понять, что а = 9
Ответ: 9
Номер: mathege
На рисунке изображён график функции `f(x) = (kx+a)/(x +b)`. Найдите k.
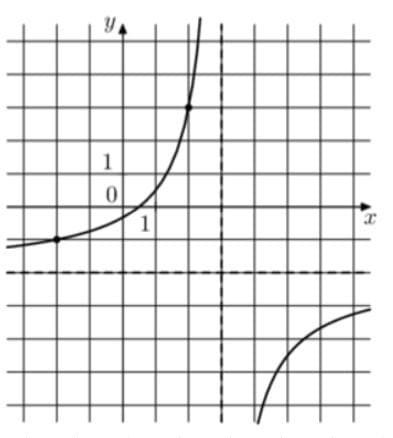
Решение:
1) b=-3 так как гипербола смещена относительно y на 3 деления вправо.
k=-5 так как функция проходит через точки в смещенной системе координат (штриховая линия) (-1;5) и (-5;1).
Кроме того добавим 1, так как штриховая система смещена относительно реальной.
Также наша функция относительно реальной и штриховой системы координат имеет смещение вниз на 2, что выражается в итоге так
`y=(-5)/(x-3)-2`
Приведем к общему знаменателю
`y=(-5-2x+6)/(x-3)=(-2x+1)/(x-3)`
Собственно, сопоставляя информацию в условии и получившемся уравнении, нетрудно понять, что а = -2
Ответ: -2
Номер: mathege
Корень
На рисунке изображён график функции `f(x) = ksqrtx`. Найдите f(6,76).
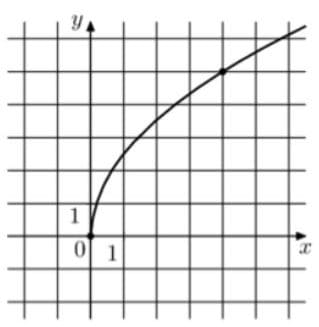
Решение:
Нам известна точка (4;5),
подставляя ее значения в функцию можем найти k
`5=k*sqrt4`
`5=2k`
`k=2,5`
получаем
`y=2,5*sqrtx`
теперь подставляем значение x=6,76 в функцию и вычисляем
`y=2,5*sqrt(6,76)=2,5*2,6=6,5`
Ответ: 6,5
Номер: mathege
На рисунке изображён график функции `f(x) = ksqrtx`. Найдите значение x, при котором f(x) = -8.
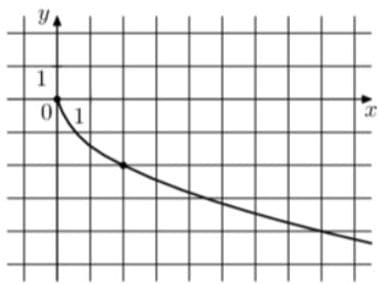
Решение:
Нам известна точка (2;-2),
подставляя ее значения в функцию можем найти k
`-2=k*sqrt2`
`k=(-2)/sqrt2`
`k=-sqrt2`
получаем
`y=-sqrt2*sqrtx`
теперь подставляем значение x=-8 в функцию и вычисляем
`-8=-sqrt2*sqrtx`
`sqrtx=(-8)/(-sqrt2)=sqrt64/sqrt2=sqrt32`
Ответ: 32
Номер: mathege
Показательная функция
На рисунке изображён график функции вида `f(x) = a^x`. Найдите значение f(3).

Решение:
Возьмём точку (1; 2), принадлежащую графику, и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а.
f(x) = ax
2 = a1
a = 2
Значит функция имеет вид:
f(x) = 2x
Найдём f(3):
f(3) = 23 = 2·2·2 = 8
Ответ: 8
Номер: EC397F
На рисунке изображён график функции вида `f(x) = a^x`. Найдите значение f(— 4).
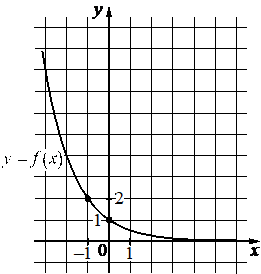
Решение:
Возьмём точку (-1; 2), принадлежащую графику, и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а.
`f(x) = a^x`
`2 = a^(-1)`
`a = 1/2`
Значит функция имеет вид:
`f(x) = (1/2)^x`
Найдём f(-4):
`f(-4) = (1/2)^-4 = 16`
Ответ: 16
Номер: 7C4A3A
На рисунке изображён график функции `f(x) = a^x+b`. Найдите f(6).
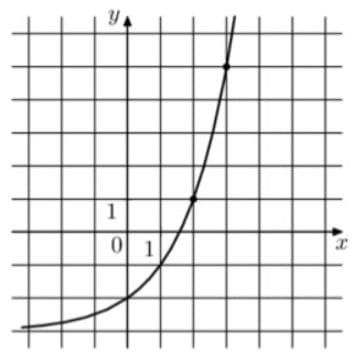
Решение:
1) Любое число в нулевой степени равно 1, значит получается, что на графике при `a^x` должно быть равно 1, но по факту проходит через -2. Получается, поправочный коэффициент b, влияющий на это, равен -3, так как 1-3=-2
2) Далее, имея значения точки графика (2;1), получаем
`f(x) = a^x+b`
`1 = a^2-3`
`a^2 = 4`
`a = 2`
В итоге функция приобретает вид
`f(x) = 2^x-3`
3) Осталось найти значения для f(6).
`f(x) = 2^6-3`
`f(x) = 64-3=61`
Ответ: 61
Номер: mathege
На рисунке изображён график функции `f(x) = a^x+b`. Найдите значение x, при котором f(x) = 12.
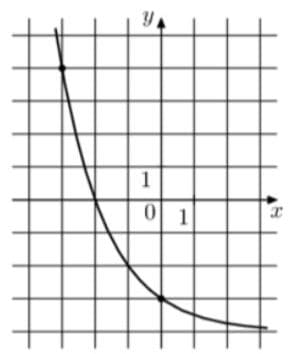
Решение:
1) Любое число в нулевой степени равно 1, значит получается, что на графике при `a^x` должно быть равно 1, но по факту проходит через -3. Получается, поправочный коэффициент b, влияющий на это, равен -4, так как 1-4=-3
2) Далее, имея значения точки графика (-3;4) получаем
`f(x) = a^x+b`
`4 = a^(-3)-4`
`1/(a^3) = 8`
`a^3 = 1/8`
`a = 1/2`
В итоге функция приобретает вид
`f(x) = (1/2)^x-4`
3) Осталось найти значения для f(12).
`12 = (1/2)^x-4`
`16 = (1/2)^x`
`2^4=(2^(-1))^x`
`2^4=2^(-x)`
`4=-x`
`x=-4`
Ответ: -4
Номер: mathege
На рисунке изображён график функции `f(x) = a^(x+b)`. Найдите f(—7).
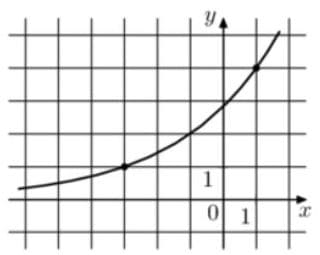
Решение:
1) Любое число в нулевой степени равно 1, значит получается, что на графике при `a^(x+b)` должно быть равно 1, если x+b=0, но по факту проходит через y=1 на три деления x левее. В этом случае поправочный коэффициент в показателе будет записываться так:
`a^(x+3)`, то есть b = 3
2) Теперь узнаем а. Берем точку (1;4)
`4=a^(1+3)`
`a^4=4`
`(a^2)^2=4`
`a=sqrt2`
`f(x) = sqrt2^(x+3)`
3) Осталось найти f(-7)
`f(-7) = sqrt2^(-7+3)`
`f(-7) = sqrt2^(-4)`
`f(-7) = 1/(sqrt2^4)`
`f(-7) = 1/((sqrt2^2)^2)`
`f(-7) = 1/4=0,25`
Ответ: 0,25
Номер: mathege
На рисунке изображён график функции `f(x) = a^(x+b)`. Найдите значение x, при котором f(x) = 0,125.
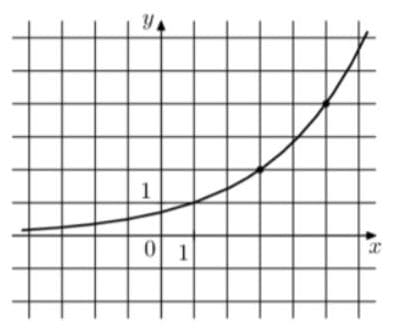
Решение:
1) Любое число в нулевой степени равно 1, значит получается, что на графике при `a^(x+b)` должно быть равно 1 при x = 0 b x+b =0, но по факту проходит через y=1 на 1 деления x правее. В этом случае поправочный коэффициент в показателе будет записываться так:
`a^(x-1)`, то есть b = -1
2) Теперь узнаем а. Берем точку (5;4)
`4=a^(5-1)`
`a^4=4`
`(a^2)^2=4`
`a=sqrt2`
`f(x) = sqrt2^(x-1)`
3) Осталось найти f(-7)
`1/8 = sqrt2^(x-1)`
`2^(-3) = (2^(1/2))^(x-1)`
`2^(-3) = 2^(1/2x-1/2)`
`-3 = 1/2x-1/2`
`-2,5 = 0,5x`
`x = -5`
Ответ: -5
Номер: mathege
Логарифмическая функция
На рисунке изображён график функции вида `f(x) = log_a x`. Найдите значение f(8).
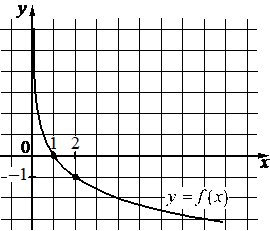
Решение:
Возьмём точку (2; –1), принадлежащую графику, и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а:
`f(x) = loga x`
`–1 = log_(a)2`
`a^(–1) = 2`
`a=1/2`
Значит функция имеет вид:
`f(x) = log_(1/2)x`
Найдём f(8):
`f(8) = log_(1/2)8=log_(2^-1)8=-1 log_(2)8=-1* 3 =-3`
Ответ: –3
Номер: DA4F4F
На рисунке изображён график функции вида `f(x) = log_a x`. Найдите значение f(16).
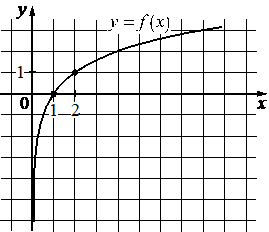
Решение:
Возьмём точку (2; 1), принадлежащую графику, и подставим её координаты х, у (это f(x)) в функцию, найдём при этом коэффициент а.
`f(x) = log_a x`
`1 = log_a 2`
`a^1 = 2`
`a = 2`
Значит функция имеет вид:
`f(x) = log_2 x`
Найдём f(16):
`f(16) = log_2 x`
`x=4`
Ответ: 4
Номер: 97C4EA
На рисунке изображён график функции вида `f(x) =b+ log_a x`. Найдите значение f(32).
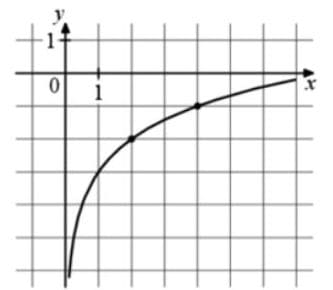
Решение:
1) Логарифмическая функция сама по себе проходит всегда через току (1;0), так как при log_2 x или log_3 x и т.д. при y = 0, x должен быть равен 1, так как любое натуральное число в нулевой степени будет давать 1.
У нас же график смещен вниз относительно 1;0, это происходит из за коэффициента b. Собственно, он и равен -3, тогда получаем:
`y =log_a x - 3`
2) Берем точку (4;-1)
`y =log_a x - 3`
`-1 =log_a 4 - 3`
`2 =log_a 4 `
`a^2=4`
`a=2`
получаем
`y=log_2 x - 3`
3) Вычисляем f(32)
`f(32) =log_2 32 - 3`
`f(32) =log_2 32 - 3 = 5-3=2`
Ответ: 2
Номер: mathege
На рисунке изображён график функции вида `f(x) =b+ log_a x`. Найдите значение x, при котором f(x) = 1.
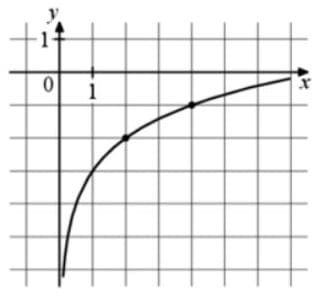
Решение:
1) Логарифмическая функция сама по себе проходит всегда через току (1;0), так как при log_2 x или log_3 x и т.д. при y = 0, x должен быть равен 1, так как любое натуральное число в нулевой степени будет давать 1.
У нас же график смещен вниз относительно 1;0, это происходит из за коэффициента b. Собственно, он и равен -3, тогда получаем:
`f(x) =log_a x - 3`
2) Берем точку (4;-1)
`y =log_a x - 3`
`-1 =log_a 4 - 3`
`2 =log_a 4 `
`a^2=4`
`a=2`
получаем
`y=log_2 x - 3`
3) Вычисляем при y =
`1 =log_2 x - 3`
`log_2 x =4`
`x =2^4`
`x =16`
Ответ: 16
Номер: mathege
На рисунке изображён график функции вида `f(x) = log_a (x+b)`. Найдите значение f(11).
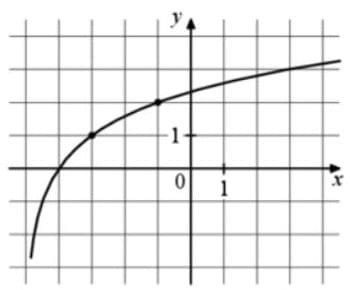
Решение:
1) Логарифмическая функция сама по себе проходит всегда через току (1;0), так как при log_2 x или log_3 x и т.д. при y = 0, x должен быть равен 1, так как любое число в нулевой степени будет давать 1.
У нас же график смещен влево относительно 1;0, это происходит из-за коэффициента b. Собственно, он и равен 5, тогда получаем:
`f(x) =log_a (x + 5)`
2) Берем точку (-1;2)
`2=log_a (-1 + 5)`
`a^2=4`
`a = 2`
получаем такую функцию
`f(x) =log_2 (x +5)`
3) Осталось посчитать ее значение при x=11
`f(11) =log_2 (x +5)`
`f(11) =log_2 (11 + 5)`
`f(11) =log_2 (16)`
`f(11) =4`
Ответ: 4
Номер: mathege
На рисунке изображён график функции вида `f(x) = log_a (x+b)`. Найдите значение x, при котором f(x)=4.
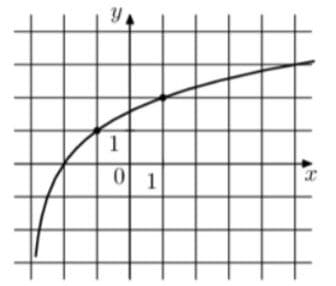
Решение:
1) Логарифмическая функция сама по себе проходит всегда через току (1;0), так как при `log_2 x` или `log_3 x` и т.д. при y = 0, x должен быть равен 1, так как любое число в нулевой степени будет давать 1.
У нас же график смещен влево относительно 1;0, это происходит из-за коэффициента b. Собственно, он и равен 3, тогда получаем:
`f(x) =log_a (x + 3)`
2) Берем точку (1;2)
`2=log_a (1 + 3)`
`a^2=4`
`a = 2`
получаем такую функцию
`f(x) =log_2 (x +3)`
3) Осталось посчитать ее значение при f(x)=4
`4 =log_2 (x +3)`
Получается два надо возвести в 4 степень, чтобы получить x +3
`16 =(x +3)`
`x = 13`
Ответ: 13
Номер: mathege
Синус
На рисунке изображён график функции f(x) = asinx + b. Найдите a.
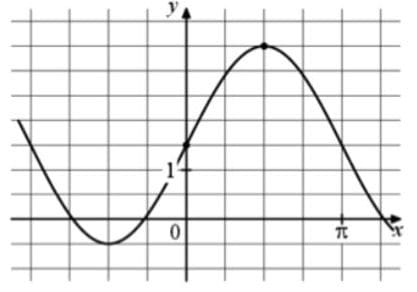
Решение:
1) Синусоида сама по себе без каких-либо коэффициентов проходит через 0;0, так как при 0 градусов синус равен 0.
У нас, как видим, завышение на 1,5, так как 3 клетки на графике именно 1,5! (будьте внимательны при масштабировании)
То есть b = 1,5
f(x) = asinx + 1,5
2) Для точки (π/2; 3)
`3,5=a*sin(π/2)+1,5`
`3,5=a*1+1,5`
`a=2`
Ответ: 2
Номер: mathege
На рисунке изображён график функции f(x) = asinx + b. Найдите b.
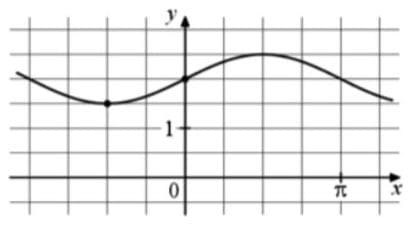
Решение:
1) Синусоида сама по себе без каких-либо коэффициентов проходит через 0;0, так как при 0 градусов синус равен 0.
У нас как видим завышение на 2, так как 4 клетки на графике именно 2! (будьте внимательны при масштабировании)
То есть b = 2
Ответ: 2
Номер: mathege
Косинус
На рисунке изображён график функции f(x) = acosx + b. Найдите a.
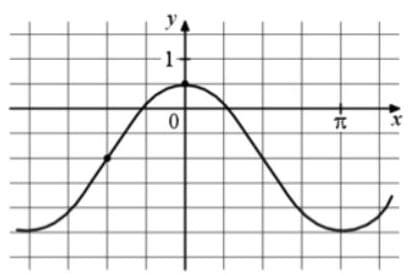
Решение:
1) График функции косинуса проходит так, что ось х посередине между минимумами и максимумами функции, то есть ее верх и низ по сути симметричен.
У нас, как видим, занижение на 1 относительно осевой горизонтали, так как 2 клетки на графике равно 1! (будьте внимательны при масштабировании)
То есть b = -1
2) Для точки (-π/2; -1)
`-1=a*cos(-π/2)-1`
так как при угле -π/2 косинус равен 0, то по факту "a" аннулируется, так как умножается на 0. В итоге берем другую точку.
Для точки (0; 1/2)
`1/2=a*cos(0)-1` cos(0) = 1
`a=1,5`
Ответ: 1,5
Номер: mathege
На рисунке изображён график функции f(x) = acosx + b. Найдите b.
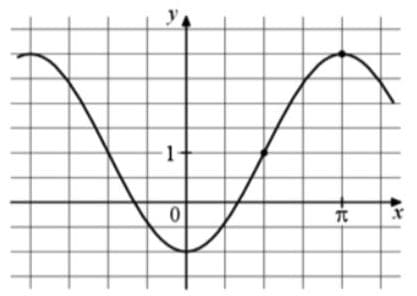
Решение:
1) У графика функции косинуса без каких-либо коэффициентов ось x находится посередине между минимумом и максимумом функции, то есть ее верх и низ по сути симметричен.
У нас завышение на 1 относительно оси x, так как 2 клетки на графике равно 1! (будьте внимательны при масштабировании)
То есть b = 1
Ответ: 1
Номер: mathege
Тангенс
На рисунке изображён график функции f(x) = atgx + b. Найдите a.
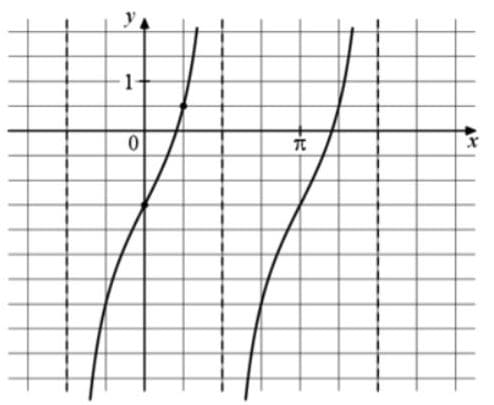
Решение:
1) Функция тангенса по горизонтальной своей оси симметрии должна совпадать с осью x. Смещение относительно оси характеризуется b. В данном случае b = -1,5
f(x) = atgx - 1,5
2) Берем точку (π/4; 1/2)
`1/2=a*tg(π/4)-1,5`
`2=a*1`
`a=2`
Ответ: 2
Номер: mathege
На рисунке изображён график функции f(x) = atgx + b. Найдите b.
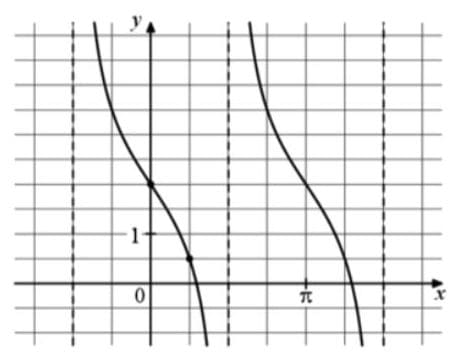
Решение:
1) Функция тангенса по горизонтальной своей оси симметрии должна совпадать с осью x. Смещение относительно оси характеризуется b. В данном случае b = 2
Ответ: 2
Номер: mathege
2 прямые
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A, Найдите абсциссу точки А.
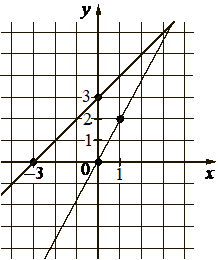
Решение:
На рисунке изображены прямые, линейных функции имеют вид:
y = kx + b
Найдём k и b первой функции.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.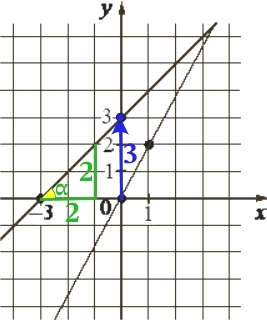
k – тангенс угла (α) наклона прямой, по отношению к оси х. Тангенс – это отношение противолежащего катета к прилежащему катету. Найдём k:
k = tg α = 2/2 = 1
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на 3.
b = 3
Первая функция имеет вид:
y = 1*x + 3 = x + 3
Найдём k и b второй функции.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.
k = tg α = 2/1 = 2
Прямая проходит через начало координат (0; 0), значит b = 0.
Вторая функция имеет вид:
`y = 2x + 0 = 2x`
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения, то есть просто приравняем полученные ранее функции:
`x + 3 = 2x`
`3 = 2x – x`
`3 = x`
Ответ: 3
Номер: 7D21DC
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
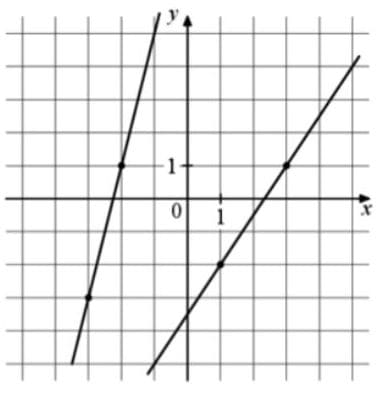
Решение:
На прямых есть выделенные точки, будем исходить из их значений.
k – тангенс угла (α) наклона прямой по отношению к оси х. Тангенс – это отношение противолежащего катета к прилежащему катету. Найдём k для двух прямых:
левая
k = tg α = 4/1 = 4
правая
k = tg α = 3/2 = 1,5
b – сдвиг прямой по оси у, по графику видим.
правая b = -3,5
левая b = 9
* эту точку на графике не видно, она выше по оси y, но ее легко высчитать если увидеть закономерность, что при смещении по оси x на 1 мы смещаемся по y на 4 вверх. Получается, в точке (-2;1) при смещении вправо по x до 0 мы сместимся вверх 2*4 = 8 на 8 делений. Итого 1+8 = 9.
В итоге, для правой получаем функцию
`y = 3/2x-3,5`
для левой
`y = 4x+9`
Теперь приравниваем наши функции, находим x
`4x+9=3/2x-3,5`
`2,5x=-12,5`
`x=-5`
Но нам надо найти ординату, то есть y, вот и ищем y(-5) для любой из функций
`y(-5) = 4x+9`
`y(-5) = 4*(-5)+9`
`y(-5) = -20+9=-11`
Ответ: -11
Номер: mathege
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
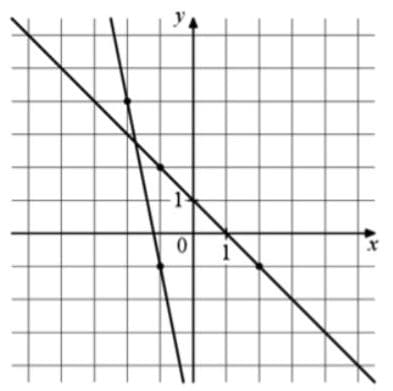
Решение:
На прямых есть выделенные точки, будем исходить из их значений.
k – тангенс угла (α) наклона прямой по отношению к оси х. Тангенс – это отношение противолежащего катета к прилежащему катету. Найдём k для двух прямых:
прямая с выделенными точками (2;-1)(-1;2)
k = tg α = 3/3 = -1 (знак минус, так как при возрастании x ось y убывает)
прямая с выделенными точками (-2;4)(-1;-1)
k = tg α = -5/1 = -5 (знак минус, так как при возрастании x ось y убывает)
b – сдвиг прямой по оси у, по графику видим.
прямая с выделенными точками (2;-1)(-1;2)
b = 1
прямая с выделенными точками (-2;4)(-1;-1)
b = - 6
* эту точку на графике не видно, она ниже по оси y, но ее легко высчитать если увидеть закономерность, что при смещении по оси x на 1 вправо мы смещаемся по y на 5 вниз.
Получаем из анализа выше две функции:
`y=-5x-6`
`y = -1x+1`
Приравниваем их, так как в их пересечении х для той и другой будет один и тот же.
`-1x+1=-5x-6`
`-7=4x`
`x=-1,75`
Ответ: -1,75
Номер: mathege
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
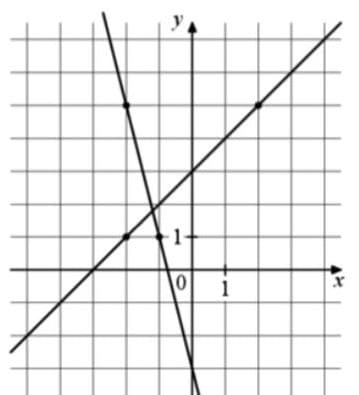
Решение:
На прямых есть выделенные точки, будем исходить из их значений.
k – тангенс угла (α) наклона прямой по отношению к оси х. Тангенс – это отношение противолежащего катета к прилежащему катету. Найдём k для двух прямых:
прямая с выделенными точками (-2;1)(2;5)
k = tg α = 4/4 = 1 (знак плюс, так как при возрастании x ось y возрастает)
прямая с выделенными точками (-1;1)(-2;5)
k = tg α = -4/1 = -4 (знак минус, так как при возрастании x ось y убывает)
b – сдвиг прямой по оси у, по графику видим.
прямая с выделенными точками (-2;1)(2;5)
b = 3
прямая с выделенными точками (-1;1)(-2;5)
b = - 3
Получаем функции:
`y=x+3`
`y=-4x-3`
Для нахождения ординаты, то есть x пересечения, приравняем функции.
`x+3=-4x-3`
`5x=-6`
`x=6/5=-1,2`
`y=-1,2+3=1,8`
Ответ: 1,8
Номер: mathege
2 параболы
На рисунке изображены графики функций `f(x) = 4x^2 — 25х + 41` и `g(x) = ах^2 + bх + с`, которые пересекаются в точках А и В. Найдите абсциссу точки В.
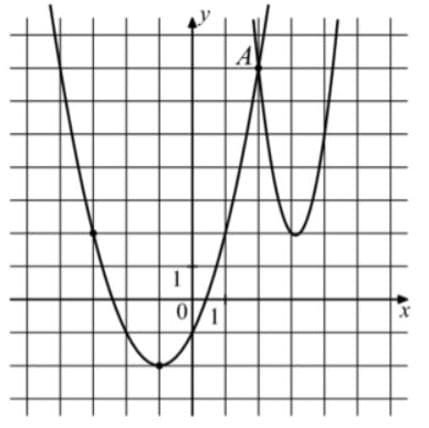
Решение:
Нам известна функция с более правой вершиной по x, это видно из анализа другой функции, так как
1) коэффициент с всегда равен координате пересечения параболы с осью Оy:
Для левой
c = -1
Для левой
a = 1
так как при возрастании x, y увеличивается квадратично, то есть без каких-либо поправочных коэффициентов.
Координата х вершины параболы находится по формуле:
`x=(-b)/(2a)`
Для точки вершины (-1;2)
`-1=(-b)/(2*1)`
`-2=-b`
`b=2`
Запишем полностью функцию
`y=1x^2+2x-1`
2) Теперь приравняем функции, чтобы найти значение абсциссы
`4x^2 — 25х + 41=1x^2+2x-1`
`3x^2-27x+42=0` |:3
`x^2-9x+14=0`
`D=81-4*1*14=25`
`x=(9+5)/2=7`
`x=(9-5)/2=2`
По условию нам надо найти пересечение в точке B. При x = 2 это точка А. Значит наш искомый x = 7
Ответ: 7
Номер: mathege
На рисунке изображены графики функций `f(x) = —2х^2 + 7x — 2` и `g(x) = ах^2 + bх + с`, которые пересекаются в точках А и В. Найдите ординату точки В.
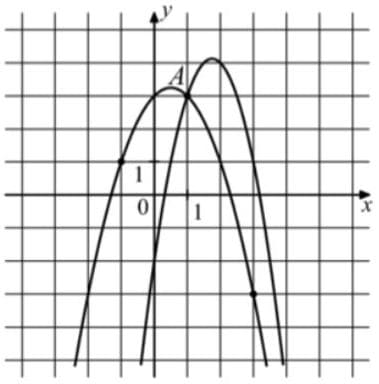
Решение:
Нам известна функция с более правой вершиной по x, это видно из анализа другой функции, так как
1) коэффициент с всегда равен координате пересечения параболы с осью Оy:
c = 3
a = -1 так как, во-первых, ветви вниз, значит отрицательный знак. Во-вторых, из системы точек (1;3) и (-1;1)
`{(3 = а*1^2 + b*1 + 3), (1 = а*(-1)^2 + b*(-1) + 3):}`
`{(1 = а*1^2 + b*1 + 1),(1 = а*(-1)^2 + b*(-1) + 3):}`
`а*(-1)^2 + b*(-1) + 3 = а*1^2 + b*1 + 1`
`- b + 3 = b + 1`
`2 b = 2`
`b = 1`
Тогда
`3 = а*1^2 + 1 + 3`
`-а*1^2 = 1`
`а = -1`
или опять же, ради проверки, из нижней функции в системе:
`1 = а*(-1)^2 - 1 + 3`
`1 = а*(-1)^2 + 2`
`-1 = а*(-1)^2`
`а = -1`
Запишем полностью функцию.
`y=-1x^2+1*x+3`
2) Найдем пересечения по x, приравняв две функции
`-2х^2 + 7x - 2 - 1x^2+1*x+3`
`х^2 -6*x+5=0`
`D=36-4*1*5=16`
`x_1=(6+4)/2=5`
`x_2=(6-4)/2=1`
Точка где x = 1 это точка A. То есть, надо найти у(5), чтобы вычислить ординату B.
`у(5) = -1x^2+1*x+3`
`у(5) = -1*5^2+5+3`
`у(5) = -25+5+3`
`у(5) = -17`
Ответ: -17
Номер: mathege
Прямая и парабола
На рисунке изображены графики функций видов `f (x) = ax^2 + bx + c` и `g(x) = kx`, пересекающиеся в точках A и В. Найдите абсциссу точки В.
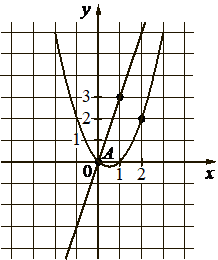
Решение:
f(x) = ax2 + bx + c
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0.
Подставим координаты точек, принадлежащих параболе, в функцию (f(x) = ax2 + bx + c):
(–1; 2) – в 1-е уравнение значения точки параболы (–1; 2),
(2; 2) – во 2-е уравнение значение точки параболы (2; 2),
и с = 0 в оба уравнения, получим систему из двух уравнений для параболы:
| 〈 | 2 = a(-1)2 + b(-1) + 0 2 = a22 + b * 2 + 0 |
| 〈 | 2 = a – b 2 = 4a + 2b поделим на 2 обе части уравнения |
| 〈 | 2 = a – b 1 = 2a + b |
Cложим уравнения:
2 + 1 = а + 2а – b + b
3 = 3a
a = 3/3 = 1
Подставим а = 1 во первое уравнение системы, найдём b:
2 = 1 – b
2 – 1 = –b
1 = –b
b = –1
Функция параболы имеет вид:
f(x) = 1* x2 – 1* x + 0 = x2 – x
Подставим точку (1; 3), принадлежащую прямой в функцию g(x) = kx и найдём k:
3 = k·1
k = 3
Функция прямой имеет вид:
g(x) = 3x
Найдём координаты абсцисс точек пересечения функций:
f(x) = g(x)
x2 – x = 3x
x2 – x – 3x = 0
x2 – 4x = 0
x(x – 4) = 0
х1 = 0 (абсцисса точки А на графике)
или
х – 4 = 0
х2 = 4 (искомая абсцисса точки В)
Ответ: 4
Номер: 3D9010
На рисунке изображены графики функций `f(x) = 5x + 9` и `g(x) = ах^2 + bx + с`, которые пересекаются в точках А и В. Найдите абсциссу точки В.
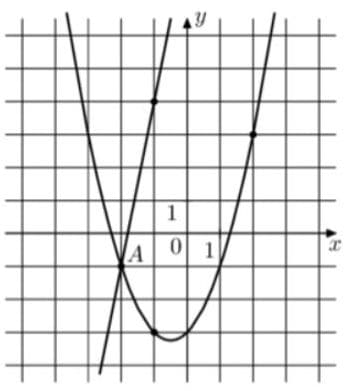
Решение:
По функции очевидно, что `f(x) = 5x + 9` это прямая, а вот квадратичная функция - это парабола. Тогда:
1) Коэффициент с всегда равен координате пересечения параболы с осью Оy:
c = -3
a = так как, во-первых, ветви вверх, значит знак +. Во-вторых, из системы точек (-1;-3) и (2;3) составляем систему уравнений и находим:
`{(-3 = а*(-1)^2 + b*(-1) - 3), (3 = а*(2)^2 + b*(2) - 3):}`
`{(-3 = а - b - 3),(3 = а*(2)^2 + b*(2) - 3):}` (из верхнего уравнения видно, что а = b), тогда
`3 = а*(2)^2 + 2a - 3`
`3 = 4а + 2a - 3`
`6a = 6`
`a =1` и `b = 1`
Получаем уравнение:
`g(x) = 1х^2 + 1x - 3`
2) Приравниваем два уравнения, чтобы получить точки пересечения по x
`5x + 9= 1х^2 + 1x - 3`
`х^2 - 4x -12 = 0`
`D= 16-4*1*(-12)=64`
`x_1=(4+8)/2=6`
`x_2=(4-8)/2=-2`
Собственно, точка пересечения с x = -2 у нас уже есть и это точка А, значит точка В со значением x = 6
Ответ: 6
Номер: mathege
На рисунке изображены графики функций `f(x) = 3x +5` и `g(x) = ax^2 + bx + с`, которые пересекаются в точках А и В. Найдите ординату точки В.
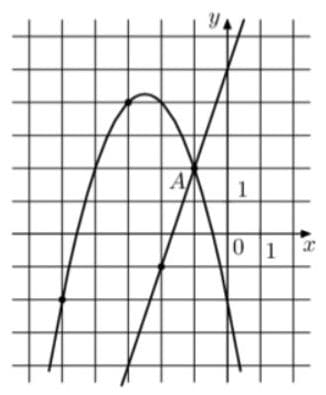
Решение:
По функции очевидно, что `f(x) = 3x +5` это прямая, а вот квадратичная функция это парабола. Тогда:
1) Коэффициент с всегда равен координате пересечения параболы с осью Оy:
c = -2
a = так как, во-первых, ветви вниз, значит знак -. Во-вторых, из системы точек (-3;4) и (-5;-2) составляем систему уравнений и находим:
`{(4 = а*(-3)^2 + b*(-3) - 2), (-2 = а*(-5)^2 + b*(-5) - 2):}`
`{(4 = 9а - 3b - 2), (-2 = 25а + 5b - 2):}`
`4 = 9а - 3b - 2`
`6 = 9а - 3b`
`3b = 9а - 6` |:3
`b = 3a - 2`
теперь подставляем в нижнее уравнение в системе выше
`-2 = а*(-5)^2 + (3a - 2)*(-5) - 2`
`0 = 25а - 15a +10`
`10a = -10`
`a=-1`
тогда b
`b = 3a - 2`
`b = 3*(-1) - 2`
`b = -5`
Получаем функцию для параболы
`g(x) = -1x^2 -5x - 2`
Приравниваем функции прямой и параболы, чтобы найти x
`3x + 5 = -1x^2 - 5x -2`
`x^2 + 8x + 7 =0`
`D= 64-4*1*7=36`
`x_1=(-8+6)/2=-1`
`x_2=(-8-6)/2=-7`
Нас интересует точка B, а значит x=-7, так как под x=-1 у нас точка А.
3) `g(-7) = 3x +5`
`g(-7) = 3*(-7) + 5`
`g(-7) = -16`
Ответ: -16
Номер: mathege
Прямая и гипербола
На рисунке изображены графики функций видов `f(x) = k/x` и `g(x) = ax + b`, пересекающиеся в точках А и B. Найдите абсциссу точки В.
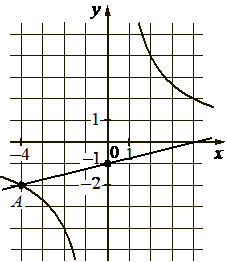
Решение:
`f(x) = k/x`
Подставим координаты точки (–4; –2), найдём k гиперболы:
`–2 = k/(–4)`
k = –2·(–4) = 8
Гипербола имеет вид:
`f(x) = 8/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой по отношению к оси х. Тангенс - это отношение противолежащего катета к прилежащему катету:
`a = tg a =1/4` = 0,25
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –1.
b = –1
Функции прямой имеет вид:
g(x) = 0,25x – 1
Найдём абсциссы точек пересечения функций:
`f(x) = g(x)`
`8 = (0,25x – 1) * x`
`8 = 0,25x^2 – x`
`0,25x^2 – x – 8 = 0`
`D = (–1)^2 – 4*0,25*(–8) = 9 = 3^2`
`x_(1)=(1+3)/(2*0.25)=8`
`x_(2)=(1-3)/(2*0.25)=-2/0.5=-4`
У точки А координата х = –4, значит у точки В координата х = 8.
Ответ: 8
Номер: CA314B
На рисунке изображены графики функций `f(x) = k/x` и `g(x) = ах + b`, которые пересекаются в
точках А и В. Найдите ординату точки В.
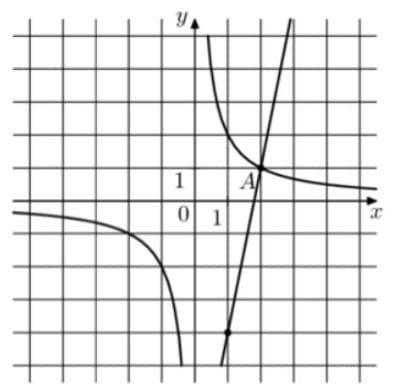
Решение:
У нас есть уравнение гиперболы `f(x) = k/x` и точка на ней (2;1). Найдем k
`f(x) = k/x`
`1 = k/2`
`k = 2`
Теперь найдем характеристики для прямой.
`g(x) = ах + b`
a - отношение возрастания y к x, то есть по факту тангенс прямоугольного треугольника, где вершины на прямой, а угол 90 градусов достраивается из вершин.
`a=5/1=5`
b - смещение по оси y. Нетрудно посчитать, что если при смещении x влево на 1 y теряет 5 вниз. Получается b = -4-5=-9
В итоге получаем прямую
`g(x) = 5х - 9`
Теперь приравниваем функции и находим x
`2/x= 5х - 9` |*x
`2 = 5х^2 - 9x`
`5х^2 - 9x - 2 = 0`
`D=81-4*5*(-2)=121`
`x_1=(9+11)/(2*5)=2`
`x_2=(9-11)/(2*5)=-0,2`
Нас интересует точка `x_2=-0,2` так как она будет B. Возьмем для нахождения значения функцию гиперболы, хотя с тем же успехом можем взять и прямую.
`f(x) = k/x`
`f(x) = 2/(-0,2) = -10`
Ответ: -10
Номер: mathege
Прямая и корень
На рисунке изображены графики функций видов `f(x) = аsqrtx` и `g(x) = kx`, пересекающиеся в точках А и В. Найдите абсциссу точки В.
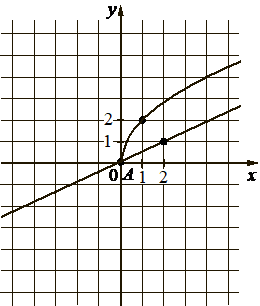
Решение:
f(x) кривой проходит через точку (1; 2), подставим значения х и у (это f(x)) в функцию, найдём а:
f(x) = a√x
2 = a√1
2 = a·1
а = 2
Значит функция имеет вид: f(x) = 2*√x
g(x) проходит через точку (2; 1), подставим значения х и у (это f(x)) в функцию, найдём k:
g(x) = kx
1 = k·2
k=1/2=0,5
Значит функция имеет вид: g(x) = 0,5x
Найдём абсциссу (х) точки пересечения В из системы уравнений:
`f(x)=2sqrt(x)`
`g(x)=0,5x`
`y=2sqrt(x)`
`y=0,5x`
Приравняем через y уравнения:
2√x = 0,5x
Возведём обе части в квадрат:
(2√x)2 = (0,5x)2
4x = 0,25x2
16x = x2
16x – x2 = 0
x*(16 – x) = 0
`x_1 = 0` (абсцисса точки А)
или
16 – x = 0
`х_2 = 16` (абсцисса точки В)
Ответ: 16
Номер: 448E90
На рисунке изображены графики функций `f(x) = аsqrtx` и `g(x) = kx + b`, которые пересекаются в точке А. Найдите абсциссу точки А.
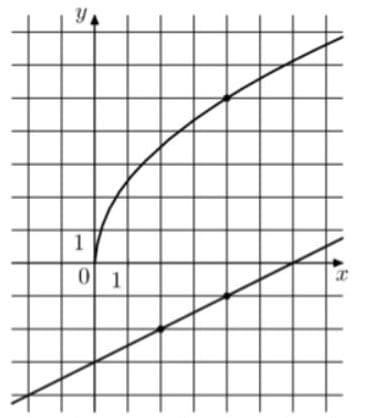
Решение:
В первую очередь, найдем a для функции корня`f(x) = аsqrtx`. Для этого возьмем отмеченную точку (4;5), подставим значения в функцию
`5=asqrt4`
`a = 5/sqrt4`
`a = 5/2=2,5`
Получаем функцию
`f(x) = 2,5sqrtx`
Теперь найдем k и b для прямой.
k – тангенс угла наклона прямой по отношению к оси х. Тангенс - это отношение противолежащего катета к прилежащему катету:
b - это смещение по оси y при x =0. b = -3.
`g(x) = kx + b`
`k=1/2=0,5`
Получаем функцию:
`g(x) = 0,5x -3`
Приравниваем функции корня и прямой, ищем точку пересечения по x
`2,5sqrtx = 0,5x -3`
`x - 6 = 5sqrtx`
пусть t=sqrtx, тогда
`t^2-5t-6=0`
`D=25-4*1*(-6)=49`
`t_1=(5+7)/2=6`
`t_2=(5-7)/2=-1`
`x=t^2 = 36` так как, глядя на график, пересечение уж точно не в точке где x = 1
Ответ: 36
Номер: mathege
На рисунке изображены графики функций `f(x) = аsqrtx` и `g(x) = kx + b`, которые пересекаются в точке А. Найдите ординату точки А.
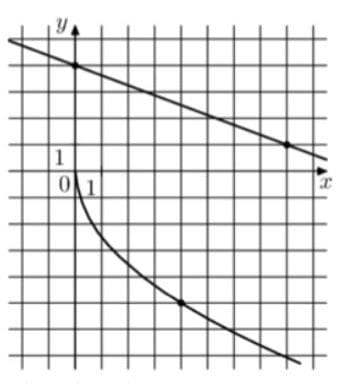
Решение:
В первую очередь найдем a для функции корня`f(x) = аsqrtx`. Для этого возьмем отмеченную точку (4;-5), подставим значения в функцию
`-5=asqrt4`
`a = -5/sqrt4`
`a = -5/2=-2,5`
Получаем функцию
`f(x) = -2,5sqrtx`
Теперь найдем k и b для прямой.
k – тангенс угла наклона прямой по отношению к оси х. Тангенс - это отношение противолежащего катета к прилежащему катету:
b - это смещение по оси y при x =0. b = 4.
`g(x) = kx + b`
`k=3/8=-0,375` знак минус, так как график функции при увеличении x идет вниз.
Получаем функцию:
`g(x) = -0,375x +4`
Приравниваем функции корня и прямой, ищем точку пересечения по x
`-2,5sqrtx = -0,375x +4`|*8
`-20sqrtx = -3x +32`
пусть t=sqrtx, тогда
`3t^2-20t-32=0`
`D=400-4*3-32=784=28^2`
`t_1=(20+28)/(2*3)=8`
`t_2=(20-28)/(2*3)=-8/6`
`x=t^2 = 64`
второй корень t не соответствует действительности. Нам же надо найти ординату, то есть подставляем 64 в значение функции для x
`g(x) = -0,375*64 +4=-20`
Ответ: -20
Номер: mathege

