На ЕГЭ по математике в заданиях из тригонометрии часто нужно перевести один угол в другой, синус в косинус и тому подобное, используя формулы приведения. Обычно учитель заставляет эти формулы выучить. Но зачем учить гору формул, когда достаточно запомнить пару правил!
Часто в задачах встречаются выражения вида `cos(x+(3π)/2)`, `sin(π/2−x)`, `tg(x+π/2)`, а также `sin(x+π)` или `cos(π−x)` — то есть такие, где к аргументу прибавляется нечетное число, умноженное на `π/2`, или целое число, умноженное на `π`. Они упрощаются с помощью формул приведения. Эти формулы называются так потому, что с их помощью можно привести выражения к более простым.
Вот эти формулы:
`cos(x+(3π)/2)=sinx`,
`cos(x+π/2)=−sinx`
`sin(π/2−x)=cosx`,
`tg(x+π/2)=−ctgx`,
`sin(x+π)=−sinx`,
`cos(π−x)=−cosx`,
`sin(x-π)=sinx`.
Зубрить наизусть формулы приведения не нужно. Достаточно действовать по алгоритму.
Алгоритм для правил приведения
1) Сначала определим ЗНАК. У получившегося выражения знак такой же, каким будет знак тригонометрической функции в левой его части, при условии, что аргумент х мы берем из первой четверти.
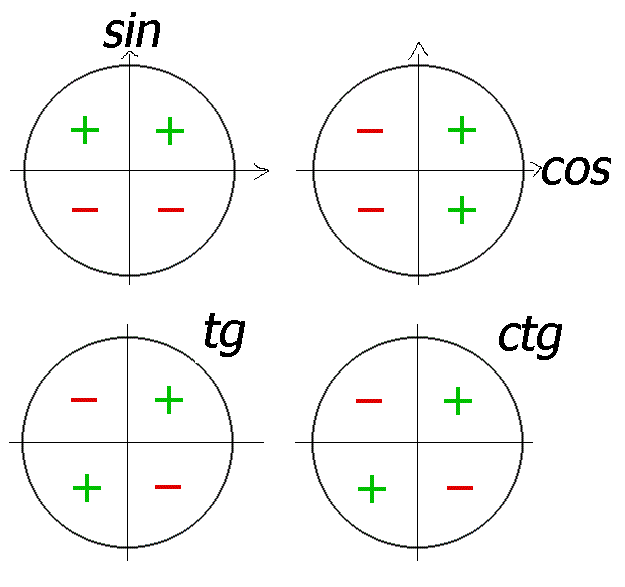
Пример. Упростим выражение `cos(x+π/2)`.
Определяем знак. Взяв x из первой четверти и прибавив к нему `π/2`, попадем во вторую четверть. Во второй четверти косинус отрицателен. Значит знак минус.
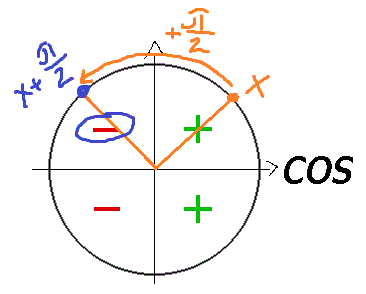
Записываем `cos(x+π/2)=− ...` , теперь нужно определить функцию.
2) Если в тригонометрической формуле к аргументу прибавляется (или вычитается из него) `π/2`, `(3π)/2`, `(7π)/2`, ... 90°, 270° ... — в общем, угол, лежащий на вертикальной оси, — функция МЕНЯЕТСЯ на кофункцию. Синус меняется на косинус, косинус на синус, тангенс на котангенс и наоборот.
Если же мы прибавляем или вычитаем `π`, `3π`, `5π`, ... 180°, 360° ... — то, что лежит на горизонтальной оси, — функция на кофункцию НЕ меняется.
А если промежуточные точки типа `(3π)/4`? А промежуточных ни в формулах приведения, ни на ЕГЭ не бывает.
Запминалка:
Если прибавляемый угол лежит на вертикальной оси — вертикально киваем головой, говорим: «Да, да, меняется функция на кофункцию». Если прибавляемый угол лежит на горизонтальной оси — горизонтально мотаем головой, говорим: «Нет, нет, не меняется функция на кофункцию».
Пример. Упростим выражение `cos(x+π/2)`.
Знак определили в пункте 1, получился минус.
Видим `π/2` ⇒ функция меняется на кофункцию — и в результате в правой части напишем синус.
В итоге получится `cos(x+π/2)=−sinx`
Но теория без практики - пустая болтовня. Давайте решим несколько заданий ЕГЭ, в которых используются формулы приведения.
Задания ЕГЭ
Посмотрим, как формулы приведения применяются в задачах ЕГЭ по математике.
1. Найдите значение выражения: `(11cos28°)/(sin62°)`.
Решение:
`(11cos28°)/(sin62°)=(11cos(90°−62°))/(sin62°)=(11sin62°)/(sin62°)=11`
Ответ: 11
2. Вычислите: `4tg18°⋅tg72°`.
Решение:
`4tg18°⋅tg72°=4tg18°⋅tg(90°−18°)=4tg18°⋅ctg18°=4`
Ответ: 4
3. Вычислите: `(12)/(sin(−(25π)/4)cos((23π)/4))`.
Тут сложность в том, что один из углов отрицательный, а это значит, что когда определяем четверть, в которой он будет находиться, ИДЕМ по кругу В ОТРИЦАТЕЛЬНУЮ СТОРОНУ! От этого будет зависеть знак функции.
Решение:
`12/(sin(−(25π)/4)cos((23π)/4))=12/(sin(−(6π+π/4))⋅cos(6π−π/4))=(12)/(−sin π/4⋅cos π/4)=−(12)/(sqrt2/2⋅sqrt2/2)=−24`
Мы упростили выражения в скобках.
`-(25π)/4=-(6π+π/4)` Пойдем по кругу из 0 вниз, потому что отрицательный угол
`(23π)/4=(24π)/4−π/4=6π−π/4` Пойдем по кругу в положительную сторону (вверх) на `6π`, а потом откатимся немного назад на `π/4`.
Ответ: - 24
4. Найдите значение выражения: `(2sin152°)/(cos76°⋅cos14°)`.
Решение:
Видим, что 152° может быть двойным углом (2*76°), раскладываем синус152 по формуле синуса двойного угла. Затем применяем формулы приведения.
`(2sin152°)/(cos76°⋅cos14°)=(4sin76°⋅cos76°)/(cos76°⋅cos14°)=(4sin76°)/(cos14°)=(4sin(90°−14°))/(cos14°)=(4cos14°)/(cos14°)=4`
Ответ: 4
5. Упростите выражение: `(3cos(π−β)+sin(π/2+β))/(cos(β+3π))`.
Решение:
`(3cos(π−β)+sin(π/2+β))/(cos(β+3π))=(−3cosβ+cosβ)/(−cosβ)=(−2cosβ)/(−cosβ)=2`.
Ответ: 2.
6. Найдите значение выражения: `(3cos(−3π−β) +sin(π/2+β))/(5cos(β+3π))`.
Решение:
Используя формулы приведения, получим
`(3cos(−3π−β) +sin(π/2+β))/(5cos(β+3π))=(3cos(−(3π+β)) +sin(π/2+β))/(5cos(β+3π))=(−3cosβ+cosβ)/(−5cosβ)=(−2cosβ)/(−5cosβ)=0,4`
Ответ: 0,4
7. Найдите значение выражения: `12sqrt2 cos(−225°)`.
Решение:
`12sqrt2 cos(−225°)=12sqrt2⋅cos(−(180°+45°))=`идем по кругу из 0 вниз, потому что отрицательный угол`=−12sqrt2⋅cos45°=−12sqrt2⋅ sqrt2/2=−12`
Ответ: -12
8. Найдите значение выражения: `(35cos11°)/(sin79°) +7`.
Решение:
Используем формулу приведения для синуса 79°.
`(35cos11°)/(sin79°) +7=(35cos11°)/(sin(90°−11°)) +7=(35cos11°)/(cos11°) +7=35+7=42`
А можно не для синуса 79°, а для косинуса 11°? Можно.
`(35cos11°)/(sin79°) +7=(35cos(90-79°))/(sin79°) +7=(35sin79°)/(sin79°) +7=35+7=42`
Ответ: 42
9. Найдите значение выражения: `38/(sin^2 51°+3+sin^2 141°)`.
Решение:
Воспользуемся формулами приведения и основным тригонометрическим тождеством (сумма квадратов синуса и косинуса угла альфа равна единице):
`38/(sin^2 51°+3+sin^2 141°)=38/(sin^2 51°+3+sin^2 (90°+51°))=38/(sin^2 51°+3+cos^2 51°)=38/4=9,5`
Ответ: 9,5
Лайфхак 1. Если видите в задании ЕГЭ кривые градусы или радианы, не относящиеся к характерным точкам тригонометрического круга, то скорее всего тут надо использовать формулы приведения!
Лайфхак 2. В заданиях краткой части эти синусы-косинусы с кривыми градусами должны сократиться. Если ответ не приводится к целому числу или десятичной дроби, ищите ошибку в решении!

