Какие задания были на ЕГЭ по профильной математике 27.05.25

Каждый год мы собираем задания, которые были на реальных ЕГЭ, чтобы пополнить свою базу заданий и помочь в подготовке ученикам, которым еще предстоит сдавать ЕГЭ. Сегодня прошла основная волна ЕГЭ по профильной математике. Уже можно подвести некоторые итоги. Как и обещал Ященко, вся первая часть была из открытого банка заданий ФИПИ, но с другими числами. Все эти задания мы разобрали и у нас на ГДЗответе, если вы готовились с нами, то эту часть вы должны были написать легко и быстро. Выкладываем задания с ЕГЭ разных регионов. Многое уже с ответами.

Реальные задания ЕГЭ по профильной математике. Основная волна 27.05

Первая часть. Условия

Задачи №1. Условия

**№1.1** (Дальний Восток)

Острый угол `B` прямоугольного треугольника `ABC` равен 67°. Найдите угол между высотой `CH` и биссектрисой `CD`, проведенными из вершины прямого угла. Ответ дайте в градусах.

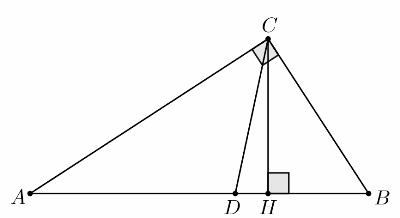
### №1.2 (Сибирь)

Острый угол `B` прямоугольного треугольника `ABC` равен 55°. Найдите угол между высотой `CH` и медианой `CM`, проведенными из вершины прямого угла `C`. Ответ дайте в градусах.

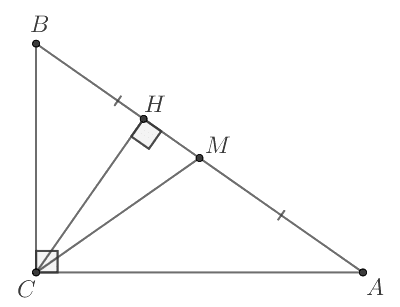
### №1.3 (центр)

В треугольнике `ABC` известно, что `AB = BC`, внешний угол при вершине `B` равен 138°. Найдите `angle C`. Ответ дайте в градусах.

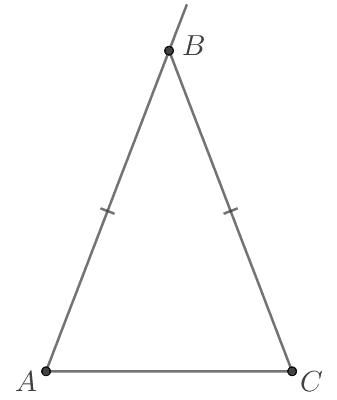
Задачи №2. Условия

**№2.1** (Дальний Восток)

Даны векторы `vec a(7; -3)` и `vec b(5; 12)`. Найдите скалярное произведение векторов `vec a` и `vec b`.

### №2.2 (Центр)

Даны векторы `vec a(1; 2)`, `vec b(-3; 6)` и `vec c(4; -2)`. Найдите длину вектора `vec a - vec b + vec c`.

Задачи №3. Условия

**№3.1 (Дальний Восток)

Около конуса описана сфера, то есть сфера содержит окружность основания конуса и его вершину. Центр
основания конуса совпадает с центром сферы, а ее радиус равен `10sqrt(2)`. Найдите образующую конуса.

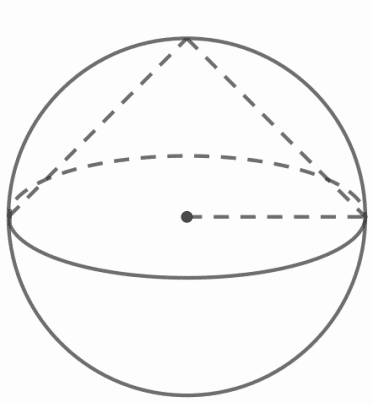
**№3.2 (Центр)

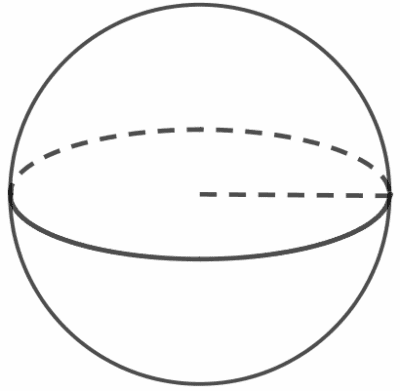
Площадь поверхности шара равна 24. Найдите площадь большого круга шара.

Задачи №4. Условия

**№4.1 (Дальний Восток)

На олимпиаде по химии 400 участников собираются разместить в четырёх аудиториях: в трёх — по 110
человек, а оставшихся — в запасной аудитории в другом корпусе. Найдите вероятность того, что случайно
выбранный участник будет писать олимпиаду в запасной аудитории.

**№4.2 (Дальний Восток (не подтверждено))

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов: первые три дня по
11 докладов, остальные распределены поровну между четвёртым и пятым днями. На конференции
планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность
того, что доклад профессора М. окажется запланированным на последний день конференции?

Задачи №5. Условия

**№5.1 (Дальний Восток)

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате
закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12.
Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

**№5.2 (Сибирь)

При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность
того, что масса окажется меньше чем 810 г, равна 0,97. Вероятность того, что масса окажется больше чем
790 г, равна 0,91. Найдите вероятность того, что масса буханки больше чем 790 г, но меньше чем 810 г.

**№5.3 (Центр)

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна,
равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что
система контроля забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке
забракует исправную батарейку, равна 0,04. Найдите вероятность того, что выбранная изготовленная
батарейка будет забракована системой контроля.

Задачи №6. Условия

**№6.1 (Дальний Восток)
Решите уравнение `7^(x-4) = 49`.

**№6.2 (Сибирь)
Найдите корень уравнения `(1/5)^(18-5x) = 25`

Задачи №7. Условия

**№7.1 (Дальний Восток)

`(log_7 13)/(log_49 13)`

Найдите значение выражения

**№7.2 (Сибирь)

`(log_9 125)/(log_9 5)`

Найдите значение выражения

**№7.3 (Сибирь)

`(log_7 32)/(log_7 2)`

Найдите значение выражения

**№7.4 (Сибирь)

`(log_2 49)/(log_2 7)`

Найдите значение выражения

Задачи №8. Условия

**№8.1 (Дальний Восток)
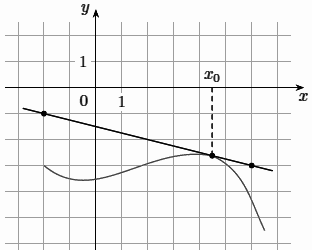
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в точке x0.

**№8.2 (Центр)**
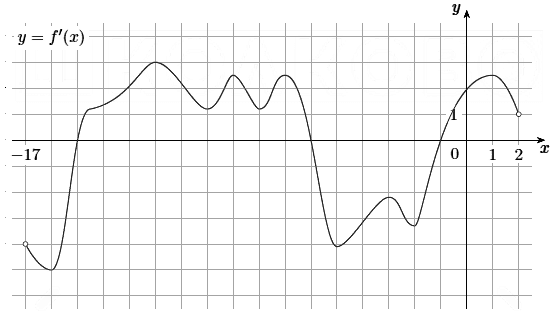
На рисунке изображен график y = f'(x) — производной функции f(x), определённой на интервале (−17; 2).
Найдите количество точек минимума функции f(x), принадлежащих отрезку [−12; 1].

Задачи №9. Условия

**№9.1 (Дальний Восток)**
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a (в км/ч^2).

Скорость v (в км/ч) вычисляется по формуле `v = sqrt(2la)`, где l — пройденный автомобилем путь (в км).
Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,8 км, приобрести скорость
100 км/ч. Ответ дайте в км/ч^2.

**№9.2 (Дальний Восток)**

должен двигаться автомобиль, чтобы, проехав 0,9 километра, приобрести скорость 150 км/ч. Ответ дайте
в км/ч^2.

Задачи №10. Условия

**№10.1 (Дальний Восток)**

От пристани А к пристани В, расстояние между которыми равно 192 км, отправился с постоянной
скоростью первый теплоход, а через 4 часа после этого следом за ним, со скоростью на 4 км/ч больше,
отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с
первым. Ответ дайте в км/ч.

**№10.2 (Сибирь)**

Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью на
24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого
автомобиля.

Задачи №11. Условия

**№11.1 (Дальний восток)**

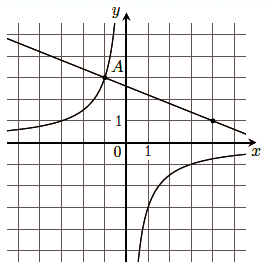
На рисунке изображены графики функций `f(x) = k/x` и `g(x) = ax + b`, которые пересекаются в точках A и
B. Найдите абсциссу точки B.

**№11.2 (Дальний Восток)**

На рисунке изображены графики функций вида `f(x) = ax + b` и `g(x) = k/x`, пересекающиеся в точках A и
B. Найдите абсциссу точки B.

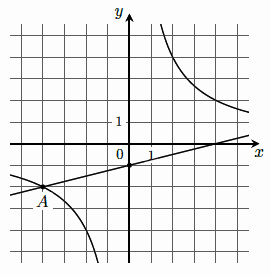
**№11.3 (Сибирь)**
На рисунке изображены графики функций видов `f(x) = ax^2 + bx + c` и `g(x) = kx`, пересекающиеся в
точках A и B. Найдите абсциссу точки B.

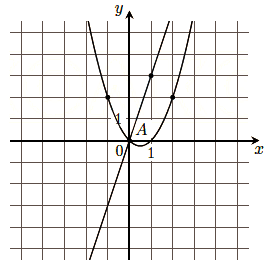
**№11.4 (Центр)**
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу
точки A.

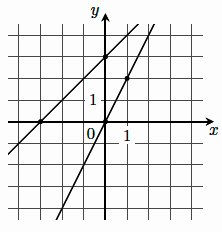
Задачи №12. Условия

**№12.1 (Дальний Восток)**
Найдите точку максимума функции `y = x^3 - 5x^2 + 7x - 5`.

Вторая часть. Условия

Задачи №13. Условия

**№13.1 (Дальний Восток)**
а) Решите уравнение `2 sin x + 2sqrt(2) sin(-x) - 4 cos^2 x = sqrt(2) - 4`.
б) Найдите все корни этого уравнения, принадлежащие отрезку `[-pi/2; pi]`.

**№13.2 (Дальний Восток)**
а) Решите уравнение `2 sin x + 2sqrt(3) sin(-x) - 4 cos^2 x = sqrt(3) - 4`.
б) Найдите все корни этого уравнения, принадлежащие отрезку `[7pi/2; pi]` [Опечатка в условии, вероятно `[2pi; 7pi/2]`].

**№13.3 (Сибирь)**
а) Решите уравнение `2 cos(2pi + 2x) - 2 + sqrt(8) sin x = -sqrt(6) + sqrt(12) sin x`.
б) Найдите все корни этого уравнения, принадлежащие отрезку `[3pi/0; 2]` [Опечатка в условии, вероятно `[0; 3pi/2]`].

**№13.4 (Центр)**
а) Решите уравнение `cos 2x + 0,75 = cos^2 x`
б) Найдите все корни этого уравнения, принадлежащие отрезку `[-4pi; -5pi/2]`.

Задачи №14. Условия

**№14.1 (Дальний восток)**
В правильной треугольной призме `ABC A_1B_1C_1` отметили точки `M` и `K` на ребрах `AA_1` и `A_1B_1`
соответственно. Известно, что `AM = 5MA_1`, `A_1K = KB_1`. Через точки `M` и `K` провели плоскость
`alpha` перпендикулярно грани `ABB_1A_1`.
а) Докажите, что плоскость `alpha` проходит через вершину `C_1`.
б) Найдите площадь сечения призмы `ABC A_1B_1C_1` плоскостью `alpha`, если все ребра призмы равны 12.

**№14.2 (Дальний восток)**
В правильной треугольной призме `ABCA_1B_1C_1` отметили точки `M` и `K` на ребрах `AA_1` и `A_1B_1`
соответственно. Известно, что `A_1M = 2AM`, `A_1K = KB_1`. Через точки `M` и `K` провели плоскость
`alpha` перпендикулярно грани `ABB_1A_1`.
а) Докажите, что плоскость `alpha` проходит через вершину `C_1`.
б) Найдите площадь сечения призмы `ABC A_1B_1C_1` плоскостью `alpha`, если все ребра призмы равны 20.

**№14.3 (Центр)**
В правильной треугольной пирамиде SABC сторона основания AB равна 3, а боковое ребро SA равно 5. На
ребре AC отмечена точка M, а на продолжении ребра BC за точку C — точка N так, что CM = CN = 1.
а) Докажите, что сечение пирамиды SABC плоскостью SNM является равнобедренным треугольником.
б) Найдите площадь сечения пирамиды SABC плоскостью SNM.

Задачи №15. Условия

**№15.1 (Дальний восток)**
Решите неравенство `(2^(3x) - 2 * 4^(x+1) + 5 * 2^(x+2) - 16)/(x - 1) > 0`.

**№15.2 (Сибирь)**
Решите неравенство `(27^x - 3 * 9^(x+1) + 3^(x+5) - 729)/(50x^2 + 10x + 0,5) < 0`.

**№15.3 (Центр)**
Решите неравенство `2/(2^x + 10) <= 3/(2^(x+1) - 1)` [Опечатка в условии, вероятно знаменатель справа `2^(x+1) - 1`].

Задачи №16. Условия

**№16.1 (Дальний восток)**
В июле планируется взять кредит в банке на сумму 14 млн рублей на некоторое целое число лет. Условия
его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплачивать часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет взят кредит, если известно, что общая сумма выплат после его погашения равнялась 24,5
млн рублей?

**№16.2 (ЕАО)**
15 декабря 2025 года планируется взять кредит в банке на сумму 18 млн рублей на 72 месяца. Условия
его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо одним платежом оплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число
предыдущего месяца;
– к 15 декабря 2031 года кредит должен быть полностью погашен.
Чему равна общая сумма платежей в 2027 году?

**№16.3 (Камчатский край)**
15 декабря 2026 года планируется взять кредит в банке на сумму 6 млн рублей на 24 месяца. Условия его
возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо одним платежом оплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число
предыдущего месяца;
– к 15 декабря 2028 года кредит должен быть полностью погашен. Чему равна общая сумма платежей в
2027 году?

**№16.4 (Камчатский край)**
15 декабря 2025 года планируется взять кредит в банке на сумму 6 млн рублей на 24 месяца. Условия его
возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо одним платежом оплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число
предыдущего месяца;
– к 15 декабря 2027 года кредит должен быть полностью погашен. Чему равна общая сумма платежей в
2027 году?

**№16.5 (Центр)**
15 декабря 2026 года планируется взять кредит в банке на 16 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо одним платежом оплатить часть долга;
– 15-го числа каждого месяца с 1-го по 15-й (с января 2027 года по март 2028 года включительно) долг
должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; – 15 марта 2028
года долг составит 200 тыс. рублей;
– 15 апреля 2028 года кредит должен быть полностью Погашен.
Какую сумму планируется взять в кредит, если общая сумма платежей после полного погашения составит
612 тыс. рублей?

Задачи №17. Условия

**№17.1 (Дальний восток)**
Дан остроугольный треугольник `ABC`. Известно, что `angle BAC = 2 angle ABC`. Точка O — центр описанной
окружности треугольника `ABC`. Вокруг треугольника `AOC` описана окружность, которая пересекает
сторону BC в точке P.
а) Докажите, что треугольники ABC и PAC подобны.
б) Найдите AB, если BC = 6 и AC = 4.

**№17.2 (Дальний восток)**
Дан остроугольный треугольник `ABC`. Известно, что `angle BAC = 2 angle ABC`. Точка O — центр описанной
окружности треугольника `ABC`. Вокруг треугольника `AOC` описана окружность, которая пересекает
сторону BC в точке P.
а) Докажите, что треугольники ABC и PAC подобны.
б) Найдите AB, если `BC = sqrt(21)` и AC = 3.

**№17.3 (Сибирь)**
В треугольнике проведены высота AH и медиана AM, угол ACB равен 30°. Точка H лежит на BM. В
треугольнике ACM проведена высота MQ. Отрезки MQ и AH пересекаются в F. Известно, что AM –
биссектриса угла HAC.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите площадь треугольника CFM, если AB = 10.

**№17.4 (Центр)**
В прямоугольном треугольнике `ABC` проведена высота `CH` из вершины прямого угла, AM и CN –
биссектрисы треугольников ACH и BCH соответственно,
а) Докажите, что прямые AM и CN перпендикулярны.
6) Найдите длину отрезка MN, если BC = 21 и `sin angle ABC = 2/5`.

Задачи №18. Условия

**№18.1 (Дальний Восток)**
Найдите все значения параметра a, при каждом из которых уравнение
`a(x - 9/x)^2 - 2(x - 9/x) - 49a + 18 = 0`
имеет ровно два различных корня.

**№18.2 (Дальний Восток)**
Найдите все значения параметра a, при каждом из которых уравнение
`a(x + 1/x)^2 + 5(x + 1/x) - 9a + 15 = 0`
имеет ровно два различных корня.

**№18.3 (Дальний Восток)**
Найдите все значения параметра a, при каждом из которых уравнение
`a(x + 4/x)^2 + 2(x + 4/x) - 49a + 14 = 0`
имеет ровно два различных корня.

**№18.4 (Сибирь)**
Найдите все значения параметра a, при каждом из которых уравнение
`(5x + |x - a^2| - 4|x + 1| - a^2)^2 + (a + 2)(5x + |x - a^2| - 4|x + 1| - a^2) + 1 = 0`
имеет ровно два различных корня.

**№18.5 (Центр)**
Найдите все значения a, при которых уравнение
`(|x - 8| - |x - a|)^2 - 7a(|x - 8| - |x - a|) + 10a^2 + 6a - 4 = 0`
имеет ровно два различных решения.

Задачи №19. Условия

**№19.1 (Дальний восток)**

На доске записано k последовательных натуральных чисел. Оказалось, что среди них чисел, делящихся
на 20, меньше, чем чисел, делящихся на 23.
а) Могло ли среди записанных чисел быть ровно три числа, делящихся на 20?
б) Могло ли среди записанных чисел быть ровно десять чисел, делящихся на 20?
в) Найдите наибольшее возможное значение k.

**№19.2 (Дальний восток)**

На доске записано k последовательных натуральных чисел. Оказалось, что среди них чисел, делящихся
на 25, меньше, чем чисел, делящихся на 29.
а) Могло ли среди записанных чисел быть ровно три числа, делящихся на 25?
б) Могло ли среди записанных чисел быть ровно десять чисел, делящихся на 25?
в) Найдите наибольшее возможное значение k.

**№19.3 (Центр)**

а) Приведите пример семизначного числа, из которого, вычёркивая цифры, можно получить каждое из
чисел: 206, 835, 930.
б) Существует ли восьмизначное число, из которого, вычёркивая цифры, можно получить каждое из
чисел: 247, 345, 586, 812?
в) Найдите наименьшее натуральное число, из которого можно получить все натуральные числа от 1 до
50 включительно, вычёркивая цифры.

Первая часть. Решения

Задачи №1. Решения

№1.1 (Дальний Восток)

Ответ: 22.

Решение. В прямоугольном треугольнике `ABC` высота `CH`, проведенная из прямого угла `angle C`, перпендикулярна гипотенузе `AB`. Из этого следует, что `angle CHB = 90^circ`.

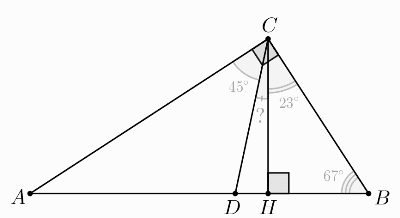
Рассмотрим прямоугольный треугольник `BCH`. Сумма его острых углов равна `90^circ`, значит,

`angle CBH + angle BCH = 90^circ`

`angle BCH = 90^circ - angle CBH = 90^circ - 67^circ = 23^circ`

В прямоугольном треугольнике `ABC` биссектриса `CD` делит прямой угол `angle C` пополам, следовательно,

`angle ACD = 1/2 angle C = 45^circ`.

Угол `DCH` — угол между высотой `CH` и биссектрисой `CD`. Получаем:

`angle ACD + angle DCH + angle BCH = 90^circ`

`angle DCH = 90^circ - (angle ACD + angle BCH) = 90^circ - (45^circ + 23^circ) = 22^circ`

Таким образом, угол между высотой `CH` и биссектрисой `CD` равен `22^circ`.

№1.2 (Сибирь)

Острый угол `B` прямоугольного треугольника `ABC` равен 55°. Найдите угол между высотой `CH` и
медианой `CM`, проведенными из вершины прямого угла `C`. Ответ дайте в градусах.

**Ответ: 20.**

**Решение. Так как медиана, опущенная из вершины прямого угла треугольника, равна половине гипоте-**
нузы, то треугольник `BMC` — равнобедренный, то есть `BM = CM`. Следовательно,

`angle BCM = angle B = 55^circ`

В прямоугольном треугольнике `BCH`:

`angle BCH = 90^circ - angle B = 35^circ`

Тогда

`angle HCM = 55^circ - 35^circ = 20^circ`

**№1.3 (центр)**

В треугольнике ABC известно, что AB = BC, внешний угол при вершине B равен 138°. Найдите `angle C`.
Ответ дайте в градусах.

**Ответ: 69.**

**Решение. Согласно теореме о внешнем угле треугольника,**

`angle A + angle C = 138^circ`

В равнобедренном треугольнике углы при основании равны, тогда

`angle A = angle C`

Таким образом,

`angle C = 138^circ : 2 = 69^circ`

Задачи №2. Решения
№2.1 (Дальний Восток)
Даны векторы `vec a(7; -3)` и `vec b(5; 12)`. Найдите скалярное произведение векторов `vec a` и `vec b`.

Ответ: `-1`.

Решение. Скалярное произведение двух векторов `vec a(x_1; y_1)` и `vec b(x_2; y_2)` равно

`vec a * vec b = x_1 x_2 + y_1 y_2`.

Следовательно, скалярное произведение наших векторов равно

`vec a * vec b = 7 * 5 + (-3) * 12 = 35 - 36 = -1`.

№2.2 (Центр)
Даны векторы `vec a(1; 2)`, `vec b(-3; 6)` и `vec c(4; -2)`. Найдите длину вектора `vec a - vec b + vec c`.

Ответ: `10`.

Решение. Найдем координаты вектора `vec r = vec a - vec b + vec c`:

`vec r(1 - (-3) + 4; 2 - 6 + (-2)) = vec r(8; -6)`

Тогда длина вектора `vec r` равна

`|vec r| = sqrt(8^2 + (-6)^2) = sqrt(100) = 10`

Задачи №3. Решения

№3.1 (Дальний Восток)
Около конуса описана сфера, то есть сфера содержит окружность основания конуса и его вершину. Центр основания конуса совпадает с центром сферы, а ее радиус равен `10sqrt(2)`. Найдите образующую конуса.

Ответ: `20`.

Решение. Рассмотрим треугольник `AOB`, где точка `O` — центр сферы, точка `A` принадлежит окружности основания конуса, точка `B` — вершина конуса. Тогда `AB` — это образующая конуса.

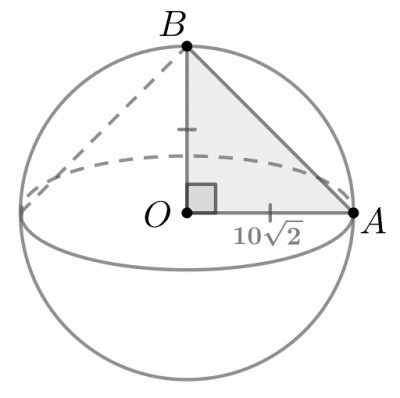
Так как центр сферы совпадает с центром основания конуса, то `BO` — высота конуса и `BO _|_ AO`. Кроме того, `AO` и `BO` — радиусы сферы. Тогда для треугольника `AOB` по теореме Пифагора имеем:

`AB^2 = AO^2 + BO^2`

`AB = sqrt(200 + 200) = 20`

**№3.2** (Центр)

Площадь поверхности шара равна 24. Найдите площадь большого круга шара.

**Ответ:** 6.

**Решение.** Площадь поверхности шара вычисляется по формуле

`S = 4 pi R^2`

Здесь `R` — радиус шара.
Площадь большого круга шара вычисляется по формуле

`S_k = pi R^2`

Здесь `R` — радиус шара.
Тогда искомая площадь равна

`S_k = pi R^2 = 1/4 * 4 pi R^2 = 1/4 S = 1/4 * 24 = 6`

Задачи №4. Решения

**№4.1** (Дальний Восток)

На олимпиаде по химии 400 участников собираются разместить в четырёх аудиториях: в трёх — по 110 человек, а оставшихся — в запасной аудитории в другом корпусе. Найдите вероятность того, что случайно выбранный участник будет писать олимпиаду в запасной аудитории.

**Ответ:** 0,175.

Решение. Найдем, сколько учеников будут писать олимпиаду в запасной аудитории:

`400 - 3 * 110 = 400 - 330 = 70`.

Тогда вероятность того, что случайно выбранный ученик будет писать олимпиаду в запасной аудитории, равна:

`p = 70/400 = 7/40 = 0,175`.

№4.2 (Дальний Восток (не подтверждено))

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов: первые три дня по 11 докладов, остальные распределены поровну между четвёртым и пятым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Ответ: 0,28.

Решение. В четвертый и пятый дни количество докладов будет равно

`(75 - 11 * 3)/2 = 21`.

Пронумеруем все 75 докладов номерами от 1 до 75. Если порядок докладов определяется жеребьевкой, то профессор М. с равной вероятностью получит один из номеров от 1 до 75. Из них 21 номер соответствует последнему дню конференции. Следовательно, искомая вероятность равна

`p = 21/75 = 7/25 = 0,28`.

Задачи №5. Решения

№5.1 (Дальний Восток)

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Ответ: 0,52.

Решение.

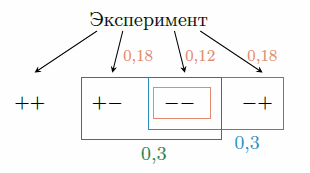
В конце дня могло возникнуть четыре различных ситуации:

- кофе остался в обоих автоматах (++);
- кофе закончился только в первом автомате (-+);
- кофе закончился только во втором автомате (+-);

- кофе закончился в обоих автоматах (--).
Это и есть ничто иное, как наши четыре элементарных исхода. По условию для каждого автомата по отдельности вероятность того, что в нем закончится кофе, равна 0,3. Значит, событию «кофе закончился в первом автомате», которое состоит из элементарных исходов `(-+)` и `(--)`, соответствует вероятность 0,3. Событию «кофе закончится в обоих автоматах» соответствует ровно один элементарный исход `(--)`. Пользуясь тем, что элементарные исходы несовместны, получаем

`P((-+)) = 0,3 - 0,12 = 0,18`.

По аналогичным соображениям

`P((+-)) = 0,3 - 0,12 = 0,18`.

Теперь легко найти вероятность интересующего нас элементарного исхода «кофе остался в обоих автоматах» (++). Вспомнив, что сумма всех элементарных исходов равна 1, получим

`P(++) = 1 - 0,18 - 0,18 - 0,12 = 0,52`.

**№5.2** (Сибирь)

При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше чем 810 г, равна 0,97. Вероятность того, что масса окажется больше чем 790 г, равна 0,91. Найдите вероятность того, что масса буханки больше чем 790 г, но меньше чем 810 г.

**Ответ:** 0,88.

**Решение.** Так как вероятность того, что масса буханки окажется меньше 810 г, равна 0,97, то вероятность того, что масса буханки окажется не меньше 810 г, равна

`p_1 = 1 - 0,97 = 0,03`.

Так как вероятность того, что масса буханки больше 790 г, равна 0,91, то вероятность того, что масса буханки не больше 790 г, равна

`p_2 = 1 - 0,91 = 0,09`.

Тогда вероятность того, что масса буханки больше 790 г и меньше 810 г, равна

`1 - p_1 - p_2 = 1 - 0,03 - 0,09 = 0,88`.

**№5.3** (Центр)

**Ответ:** 0,086.

**Решение.** Выберем произвольную батарейку. Нам удовлетворяют два случая: либо батарейка исправна, но система по ошибке ее забраковала (событие A), либо батарейка неисправна и система ее забраковала (событие B).

Так как это событие имеет вид «событие A или событие B», причем события несовместны, то вероятность его наступления равна сумме вероятностей событий A и B:

`P = P(A) + P(B)`

Найдем отдельно `P(A)` и `P(B)`.

1) Событие A = батарейка исправна и система по ошибке ее забраковала.
Следовательно, вероятность события A равна произведению вероятностей событий «батарейка исправна» и «система забраковала». Так как вероятность того, что батарейка неисправна, равна 0,05, то вероятность того, что она исправна, равна

`1 - 0,05 = 0,95`

Следовательно,

`P(A) = 0,95 * 0,04 = 0,038`

2) Событие B = батарейка неисправна и система ее забраковала.
Следовательно, вероятность события B равна произведению вероятностей событий «батарейка неисправна» и «система забраковала». Следовательно,

`P(B) = 0,05 * 0,96 = 0,048`

Таким образом, искомая вероятность равна

`P = 0,038 + 0,048 = 0,086`

Задачи №6. Решения
№6.1 (Дальний Восток)
Решите уравнение `7^(x-4) = 49`.

Ответ: `6`.

Решение. По свойствам степени имеем:

`7^(x-4) = 49`
`7^(x-4) = 7^2`
`x - 4 = 2`
`x = 6`

№6.2 (Сибирь)
Найдите корень уравнения

`(1/5)^(18-5x) = 25`

Ответ: `4`.

Решение. ОДЗ: `x` – произвольное. Решим на ОДЗ:
Исходное уравнение есть

`(1/5)^(18-5x) = (1/5)^(-2)` [так как `25 = (1/5)^(-2)`]

Оно имеет стандартный вид и равносильно `18 - 5x = -2`, что равносильно `x = 4` – подходит по ОДЗ.

Задачи №7. Решения
№7.1 (Дальний Восток)
Найдите значение выражения `(log_7 13)/(log_49 13)`.

Ответ: `2`.

Решение.
`(log_7 13)/(log_49 13) = (log_7 13)/(1/2 log_7 13) = 2`.

№7.2 (Сибирь)
Найдите значение выражения `(log_9 125)/(log_9 5)`.

Ответ: `3`.

Решение. По формуле перехода к новому основанию `(log_a b)/(log_a c) = log_c b` исходное выражение равно `log_5 125 = 3`.

№7.3 (Сибирь)
Найдите значение выражения `(log_7 32)/(log_7 2)`.

Ответ: `5`.

Решение. По формуле перехода к новому основанию `(log_a b)/(log_a c) = log_c b` исходное выражение равно `log_2 32 = 5`.

№7.4 (Сибирь)
Найдите значение выражения `(log_2 49)/(log_2 7)`.

Ответ: `2`.

Решение. По формуле перехода к новому основанию `(log_a b)/(log_a c) = log_c b` исходное выражение равно `log_7 49 = 2`.

Задачи №8. Решения

**№8.1 (Дальний Восток)**
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в точке x0.

**Ответ:** `-0,25`.

**Решение. Производная функции в точке с абциссой x0 равна тангенсу угла наклона касательной к**
графику функции в этой точке.
Если прямая проходит через точки `(x_1; y_1)` и `(x_2; y_2)`, то тангенс угла наклона этой прямой равен
`(y_2 - y_1)/(x_2 - x_1)`.

По картинке видно, что касательная проходит через точки `(-2; -1)` и `(6; -3)`.
Тогда имеем:

`f'(x_0) = (-1 - (-3))/(-2 - 6) = 2 / (-8) = -1/4 = -0,25`

**Ответ:** `1`.

**Решение. В точке минимума функции её производная обнуляется и меняет знак с «-» на «+» при**
движении слева направо, так как до точки минимума функция убывала, а после — начала возрастать.
На отрезке [−12; 1] производная обнуляется два раза — в точках

`x_1 = -6`, `x_2 = -1`

В точке `x_1 = -6` производная поменяла знак с «+» на «-» (точка максимума).
В точке `x_2 = -1` производная поменяла знак с «-» на «+».
Значит, `x_2 = -1` — единственная точка минимума на отрезке [−12; 1].

**Задачи №9. Решения**

**№9.1 (Дальний Восток)**

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a (в км/ч^2).

**Ответ:** `6250`.

**Решение. Подставим данные в формулу:**

`100 = sqrt(2 * 0,8 * a)`

`100^2 = 2 * 0,8 * a`

`10000 = 1,6a`

`a = 10000 / 1,6 = 6250`

**№9.2 (Дальний Восток)**

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч^2. Скорость v
вычисляется по формуле `v = sqrt(2la)`, где l — пройденный автомобилем путь. Найдите ускорение, с которым
должен двигаться автомобиль, чтобы, проехав 0,9 километра, приобрести скорость 150 км/ч. Ответ дайте
в км/ч^2.

**Ответ:** `12500`.

**Решение. Подставим данные в формулу:**

`150 = sqrt(2 * 0,9 * a)`

`150^2 = 2 * 0,9 * a`

`22500 = 1,8a`

`a = 22500 / 1,8 = 12500`

**Задачи №10. Решения**

**№10.1 (Дальний Восток)**

**Ответ:** `16`.

**Решение. Пусть скорость второго теплохода равна x км/ч, при этом x > 4. Составим таблицу:

|Скорость, км/ч| Время, ч| Расстояние, км|
|Первый теплоход|`x - 4`| `192/(x - 4)` | 192 |
|Второй теплоход|`x` | `192/x` |192 |

Так как второй теплоход вышел на 4 часа позже, то его время на 4 часа меньше. Составим уравнение:

`192/(x - 4) - 192/x = 4`

`(192x - 192(x - 4))/(x(x - 4)) = 4`

`(192 * 4)/(x(x - 4)) = 4`

Так как `x != 0`, `x != 4`, то можем домножить обе части уравнения на `x(x - 4)`, получим:

`192 * 4 = 4 * x(x - 4)` | :4

`192 = x(x - 4)`

`x^2 - 4x - 192 = 0`

Найдем дискриминант:

`D = (-4)^2 - 4 * 1 * (-192) = 16 + 768 = 784 = 28^2`.

Тогда корни квадратного уравнения равны

`x_1 = (4 + 28)/2 = 16`, `x_2 = (4 - 28)/2 = -12`.

Так как `x > 4`, то скорость второго теплохода равна 16 км/ч.

**№10.2 (Сибирь)**

Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью на 24 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найдите скорость первого автомобиля.

**Ответ:** `84`.

**Решение.** Обозначим искомую скорость первого автомобиля за `x`. Тогда скорость второго автомобиля равна `(x - 24)` км/ч.

Найдем время, за которое автомобили преодолевают 420 километров. Для первого это `420/x` часов, для второго — `420/(x - 24)` часов. По условию первый автомобиль прибывает к финишу на 2 часа раньше второго, имеем уравнение:

`420/x + 2 = 420/(x - 24)`

`(420 + 2x)/x = 420/(x - 24)`

`(420 + 2x)(x - 24) = 420x`

`420x - 420*24 + 2x^2 - 48x = 420x`

`2x^2 - 48x - 10080 = 0` | :2

`x^2 - 24x - 5040 = 0`

`D = (-24)^2 - 4*1*(-5040) = 576 + 20160 = 20736 = 144^2`

Отсюда

`x = (24 + 144)/2 = 168/2 = 84` или `x = (24 - 144)/2 = -120/2 = -60`

Скорость – величина неотрицательная, поэтому нам подходит ответ `x = 84` км/ч.

Задачи №11. Решения

№11.1 (Дальний восток)

На рисунке изображены графики функций `f(x) = k/x` и `g(x) = ax + b`, которые пересекаются в точках `A` и `B`. Найдите абсциссу точки `B`.

Ответ: `7,5`.

Решение. Найдём уравнение прямой. Коэффициент `a` определим по формуле

`a = (y_2 - y_1)/(x_2 - x_1)`,

где `(x_1; y_1)`, `(x_2; y_2)` — любые две точки на прямой.
По рисунку видно, что прямая проходит через точки `(-1; 3)` и `(4; 1)`. Тогда

`a = (1 - 3)/(4 - (-1)) = (-2)/5 = -2/5`.

Таким образом, получим уравнение прямой

`g(x) = -2/5 x + b`.

Чтобы найти `b`, подставим одну из точек в наше уравнение, например, точку `(4; 1)`. Её координаты обратят уравнение функции в верное равенство:

`g(4) = 1`

`-2/5 * 4 + b = 1`

`-8/5 + b = 1`

`b = 1 + 8/5 = 13/5`

Значит,

`g(x) = -2/5 x + 13/5`.

Найдём уравнение гиперболы. Она проходит через точку `(-1; 3)`, значит, её координаты обратят уравнение.

функции в верное равенство:

`f(-1) = 3`

`k / (-1) = 3`

`k = -3`

Получили

`f(x) = -3/x`.

Чтобы найти координаты точки `B`, решим уравнение `f(x) = g(x)` :

`-3/x = -2/5 x + 13/5`

Умножим обе части на `5x`:

`-15 = -2x^2 + 13x`

`2x^2 - 13x - 15 = 0`

`(x + 1)(2x - 15) = 0` [факторизация]

`x = -1`
`x = 15/2 = 7,5`

Значение `x = -1` — это абсцисса точки `A`, тогда `x = 7,5` — это абсцисса точки `B`.

№11.2** (Дальний Восток)

На рисунке изображены графики функций вида `f(x) = ax + b` и `g(x) = k/x`, пересекающиеся в точках `A` и `B`. Найдите абсциссу точки `B`.

**Ответ:** `8`.

**Решение.** Для начала рассмотрим функцию `g(x)`:

`g(-4) = -2` `=>` `k / (-4) = -2` `=>` `k = 8`

Переходим к функции `f(x)`. Видим, что `b = -1`, так как прямая пересекает ось ординат в точке `(0; -1)`. Подставив координаты точки `(-4; -2)` в уравнение `f(x) = ax - 1`, получим `-2 = a * (-4) - 1`, откуда `a = 0,25`.

Приравниваем восстановленные функции:

`8/x = 0,25x - 1`

Умножим обе части на `x`:

`8 = 0,25x^2 - x`

`0,25x^2 - x - 8 = 0` | *4

`x^2 - 4x - 32 = 0`

`(x + 4)(x - 8) = 0`

`x_1 = -4`
`x_2 = 8`

Точка пересечения графиков с абсциссой `x = -4` уже изображена на рисунке, поэтому нам подходит точка с абсциссой `x = 8`.

№11.3 (Сибирь)

На рисунке изображены графики функций видов `f(x) = ax^2 + bx + c` и `g(x) = kx`, пересекающиеся в точках `A` и `B`. Найдите абсциссу точки `B`.

Ответ: `4`.

Решение. Начнем с параболы:
`f(0) = 0`, поэтому коэффициент `c = 0`.
`f(-1) = 2` `=>` `a(-1)^2 + b(-1) + c = 2` `=>` `a - b = 2` `=>` `a = 2 + b`,
`f(2) = 2` `=>` `a(2)^2 + b(2) + c = 2` `=>` `4a + 2b = 2` `=>` `4(2 + b) + 2b = 2` `=>` `8 + 6b = 2` `=>` `b = -1`,
`a = 2 - 1 = 1` `=>` `f(x) = x^2 - x`.

Прямая:
`g(1) = 3` `=>` `3 = k * 1` `=>` `k = 3` `=>` `g(x) = 3x`.

Приравниваем две функции:

`x^2 - x = 3x`

`x^2 - 4x = 0`

`x(x - 4) = 0`

`x_1 = 0`, `x_2 = 4`.

Точка пересечения `x = 0` у нас уже изображена на рисунке, поэтому нам подходит точка `x = 4`.

№11.4 (Центр)

На рисунке изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу
точки A.

**Ответ:** `3`.

**Решение. Найдем уравнения прямых.**
Определим коэффициенты k и b для нижней прямой. Найдём k как тангенс угла наклона прямой:

`k = (Delta y)/(Delta x) = (2 - 0)/(1 - 0) = 2/1 = 2`

Чтобы найти b, подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом k.
Подставим точку (1; 2):

`2 = 2 * 1 + b` `=>` `2 = 2 + b` `=>` `b = 0`

Значит, первая функция имеет вид `f_1(x) = 2x`.
Теперь определим коэффициенты k и b для верхней прямой. Найдём k как тангенс угла наклона прямой:

`k = (Delta y)/(Delta x) = (0 - (-3))/(-3 - 0) = 3 / (-3) = -1` [Опечатка в решении, вероятно ошибка в точках. По описанию: точки (-3,0) и (0,3) -> `k = (3 - 0)/(0 - (-3)) = 1`]

Чтобы найти b, подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом k.
Подставим точку (-3; 0):

`0 = 1 * (-3) + b` `=>` `0 = -3 + b` `=>` `b = 3`

Значит, вторая функция имеет вид

`f_2(x) = x + 3`

Теперь найдем абсциссу точки пересечения двух прямых.

`f_1(x) = f_2(x)` `<=>` `2x = x + 3` `<=>` `x = 3`

Задачи №12. Решения

№12.1 (Дальний Восток)
Найдите точку максимума функции `y = x^3 - 5x^2 + 7x - 5`.

**Ответ:** `1`.

**Решение. Функция определена при всех `x in RR`. Исследуем функцию и найдем ее промежутки возрастания

и убывания, для этого найдем ее производную:

`y' = 3x^2 - 10x + 7`

Найдем нули производной:

`y' = 0` `=>` `3x^2 - 10x + 7 = 0`
`D = (-10)^2 - 4 * 3 * 7 = 100 - 84 = 16`
`x = (10 +- 4)/6`
`x_1 = 14/6 = 7/3`, `x_2 = 6/6 = 1`

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

Интервалы: `(-oo; 1)`, `(1; 7/3)`, `(7/3; +oo)`
Знаки производной:
- На `(-oo; 1)`: `y'(0) = 3*0 - 0 + 7 = 7 > 0` -> возрастает
- На `(1; 7/3)`: `y'(1.5) = 3*(2.25) - 10*1.5 + 7 = 6.75 - 15 + 7 = -1.25 < 0` -> убывает
- На `(7/3; +oo)`: `y'(3) = 3*9 - 10*3 + 7 = 27 - 30 + 7 = 4 > 0` -> возрастает

Следовательно, `x = 1` является точкой максимума.

Вторая часть. Решения

Задачи №13. Решения

№13.1 (Дальний Восток)

a) Решите уравнение `2 sin x + 2sqrt(2) sin(-x) - 4 cos^2 x = sqrt(2) - 4`.

б) Найдите все корни этого уравнения, принадлежащие отрезку `[-pi/2; pi]`.

Ответ: a) `pi/4 + 2pi k`; `3pi/4 + 2pi k`; `-pi/6 + 2pi k`; `-5pi/6 + 2pi k`, `k in ZZ`

б) `-pi/6`; `pi/4`; `3pi/4`.

Решение. По основному тригонометрическому тождеству `cos^2 x = 1 - sin^2 x`. Тогда уравнение принимает вид:

`2 sin x + 2sqrt(2) * (-sin x) - 4(1 - sin^2 x) = sqrt(2) - 4`

`2 sin x - 2sqrt(2) sin x - 4 + 4 sin^2 x = sqrt(2) - 4`

`4 sin^2 x + (2 - 2sqrt(2)) sin x - sqrt(2) = 0` [Перенесем все влево]

Факторизуем:

`(2 sin x - sqrt(2))(2 sin x + 1) = 0` [Как в решении]

`2 sin x - sqrt(2) = 0 `=> `sin x = sqrt(2)/2` `2 sin x + 1 = 0` => `sin x = -1/2`

Решения:
`sin x = sqrt(2)/2` => `x = pi/4 + 2pi k`, `x = 3pi/4 + 2pi k`, `k in ZZ`
`sin x = -1/2` => `x = -pi/6 + 2pi k`, `x = -5pi/6 + 2pi k`, `k in ZZ`

б) Отберем корни на тригонометрической окружности. Для этого отметим на ней дугу, соответствующую отрезку `[-pi/2; pi]`, концы этой дуги и лежащие на ней точки серий решений из пункта a).

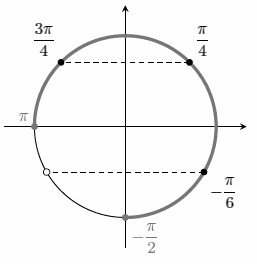
- `-pi/6 in [-pi/2; pi]`
- `pi/4 in [-pi/2; pi]`
- `3pi/4 in [-pi/2; pi]`
- `-5pi/6 = -150^circ < -90^circ = -pi/2` - не входит
- Остальные корни серий выходят за пределы отрезка.

Следовательно, на отрезке `[-pi/2; pi]` лежат точки `-pi/6`, `pi/4`, `3pi/4`.

**№13.2** (Дальний Восток)

a) Решите уравнение `2 sin x + 2sqrt(3) sin(-x) - 4 cos^2 x = sqrt(3) - 4`.

б) Найдите все корни этого уравнения, принадлежащие отрезку `[2pi; (7pi)/2]`.

**Ответ:** a) `pi/3 + 2pi k`; `2pi/3 + 2pi k`; `-pi/6 + 2pi k`; `-5pi/6 + 2pi k`, `k in ZZ`

б) `7pi/3`, `8pi/3`, `19pi/6`.

**Решение.** По основному тригонометрическому тождеству `cos^2 x = 1 - sin^2 x`. Тогда уравнение принимает вид:

`2 sin x + 2sqrt(3) * (-sin x) - 4(1 - sin^2 x) = sqrt(3) - 4`
`2 sin x - 2sqrt(3) sin x - 4 + 4 sin^2 x = sqrt(3) - 4`
`4 sin^2 x + (2 - 2sqrt(3)) sin x - sqrt(3) = 0`

Факторизуем:

`(2 sin x - sqrt(3))(2 sin x + 1) = 0`

`2 sin x - sqrt(3) = 0` => `sin x = sqrt(3)/2` `2 sin x + 1 = 0` => `sin x = -1/2`

Решения:
`sin x = sqrt(3)/2` => `x = pi/3 + 2pi k`, `x = 2pi/3 + 2pi k`, `k in ZZ`
`sin x = -1/2` => `x = -pi/6 + 2pi k`, `x = -5pi/6 + 2pi k`, `k in ZZ`

б) Отберем корни на отрезке `[2pi; 7pi/2]` (7pi/2 = 3.5pi ≈ 11.0):

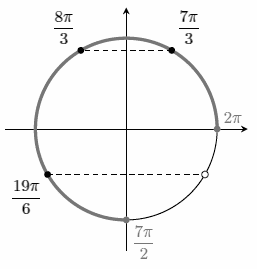
- Для `x = pi/3 + 2pi k`:
`k=3`: `pi/3 + 6pi = 19pi/3 ≈ 19.94 > 11.0` -> нет
`k=2`: `pi/3 + 4pi = 13pi/3 ≈ 13.61 > 11.0` -> нет
`k=1`: `pi/3 + 2pi = 7pi/3 ≈ 7.33 in [2pi≈6.28; 11.0]` -> подходит
- Для `x = 2pi/3 + 2pi k`:
`k=1`: `2pi/3 + 2pi = 8pi/3 ≈ 8.38 in [6.28; 11.0]` -> подходит
`k=2`: `2pi/3 + 4pi = 14pi/3 ≈ 14.66 > 11.0` -> нет
- Для `x = -pi/6 + 2pi k`:
`k=2`: `-pi/6 + 4pi = 23pi/6 ≈ 12.04 in [6.28; 11.0]?` 12.04 > 11.0 -> нет
`k=1`: `-pi/6 + 2pi = 11pi/6 ≈ 5.76 < 6.28` -> нет
`k=3`: `-pi/6 + 6pi = 35pi/6 ≈ 18.33 > 11.0` -> нет
- Для `x = -5pi/6 + 2pi k`:
`k=2`: `-5pi/6 + 4pi = 19pi/6 ≈ 9.95 in [6.28; 11.0]` -> подходит
`k=3`: `-5pi/6 + 6pi = 31pi/6 ≈ 16.22 > 11.0` -> нет

Итак, корни: `7pi/3`, `8pi/3`, `19pi/6`.

**№13.3** (Сибирь)

a) Решите уравнение `2 cos(2pi + 2x) - 2 + sqrt(8) sin x = -sqrt(6) + sqrt(12) sin x`. [Упростим: `cos(2pi + 2x) = cos(2x)`, `sqrt(8)=2sqrt(2)`, `sqrt(12)=2sqrt(3)`]

б) Найдите все корни этого уравнения, принадлежащие отрезку `[0; (3pi)/2]`.

**Ответ:** a) `-pi/3 + 2pi k`, `-2pi/3 + 2pi k`, `pi/4 + 2pi k`, `3pi/4 + 2pi k`, `k in ZZ`

б) `pi/4`, `3pi/4`, `4pi/3`.

**Решение.** a) Используя формулу косинуса двойного угла и периодичность косинуса, преобразуем уравнение:

`2 cos(2x) - 2 + 2sqrt(2) sin x = -sqrt(6) + 2sqrt(3) sin x`

Перенесем все влево:

`2 cos(2x) - 2 + 2sqrt(2) sin x + sqrt(6) - 2sqrt(3) sin x = 0`

Используем тождество `cos(2x) = 1 - 2 sin^2 x`:

`2(1 - 2 sin^2 x) - 2 + (2sqrt(2) - 2sqrt(3)) sin x + sqrt(6) = 0`

`2 - 4 sin^2 x - 2 + 2(sqrt(2) - sqrt(3)) sin x + sqrt(6) = 0`

`-4 sin^2 x + 2(sqrt(2) - sqrt(3)) sin x + sqrt(6) = 0` | *(-1)

`4 sin^2 x - 2(sqrt(2) - sqrt(3)) sin x - sqrt(6) = 0`

Факторизуем (как в решении):

`(2 sin x + sqrt(3))(2 sin x - sqrt(2)) = 0` [Проверка: `2sinx*2sinx = 4sin^2x`, свободный член `sqrt(3)*(-sqrt(2)) = -sqrt(6)`, коэффициент при sinx: `2sinx*(-sqrt(2)) + 2sinx*sqrt(3) = 2sinx(sqrt(3) - sqrt(2))`, что совпадает с `-2(sqrt(2) - sqrt(3)) sin x = 2(sqrt(3) - sqrt(2)) sin x`]

Таким образом, мы получаем

`2 sin x + sqrt(3) = 0` => `sin x = -sqrt(3)/2` `2 sin x - sqrt(2)) = 0` => `sin x = sqrt(2)/2`

Решения:
`sin x = -sqrt(3)/2` => `x = -pi/3 + 2pi k`, `x = -2pi/3 + 2pi k`, `k in ZZ`
`sin x = sqrt(2)/2` => `x = pi/4 + 2pi k`, `x = 3pi/4 + 2pi k`, `k in ZZ`

б) Отберем корни на отрезке `[0; 3pi/2]`:

- `pi/4 ≈ 0.785 in [0; 4.71]`
- `3pi/4 ≈ 2.356 in [0; 4.71]`
- `-pi/3 + 2pi = 5pi/3 ≈ 5.236 > 4.71` -> нет
- `-2pi/3 + 2pi = 4pi/3 ≈ 4.189 in [0; 4.71]` -> подходит (это 240°)
- Другие корни серий выходят за пределы.

Следовательно, на отрезке `[0; 3pi/2]` лежат точки `pi/4`, `3pi/4`, `4pi/3`.

**№13.4** (Центр)

a) Решите уравнение `cos 2x + 0,75 = cos^2 x`
б) Найдите все корни этого уравнения, принадлежащие отрезку `[-4pi; -5pi/2]`.

**Ответ:** `-11pi/3`, `-10pi/3`, `-8pi/3`.

Решение. a) Преобразуем уравнение:
`cos 2x + 3/4 = cos^2 x`
Используем тождество `cos 2x = 2 cos^2 x - 1`:
`2 cos^2 x - 1 + 3/4 = cos^2 x`
`2 cos^2 x - cos^2 x = 1 - 3/4`
`cos^2 x = 1/4`
`cos x = +- 1/2`

Решения:
`cos x = 1/2` => `x = +- pi/3 + 2pi k`, `k in ZZ`
`cos x = -1/2` => `x = +- (2pi)/3 + 2pi k`, `k in ZZ`

б) Отберем корни на отрезке `[-4pi; -5pi/2]` (≈ [-12.566; -7.854]):
Объединим серии: `x = +- pi/3 + 2pi k`, `x = +- (2pi)/3 + 2pi k` = `x = pi/3 + 2pi k`, `x = -pi/3 + 2pi k`, `x = (2pi)/3 + 2pi k`, `x = -(2pi)/3 + 2pi k`.

Подберем k так, чтобы x попало в `[-4pi; -5pi/2]`:
- Для `x = pi/3 + 2pi k`:
`k = -3`: `pi/3 - 6pi = (1/3 - 6)pi = -17pi/3 ≈ -17.80 < -12.57` -> нет
`k = -2`: `pi/3 - 4pi = (1/3 - 4)pi = -11pi/3 ≈ -11.52 in [-12.57; -7.85]` -> да
- Для `x = -pi/3 + 2pi k`:
`k = -2`: `-pi/3 - 4pi = -13pi/3 ≈ -13.61 < -12.57` -> нет
`k = -1`: `-pi/3 - 2pi = -7pi/3 ≈ -7.33 > -7.85` -> нет (нижняя граница -12.57)
- Для `x = (2pi)/3 + 2pi k`:
`k = -2`: `(2pi)/3 - 4pi = (2/3 - 4)pi = -10pi/3 ≈ -10.47 in [-12.57; -7.85]` -> да
- Для `x = -(2pi)/3 + 2pi k`:
`k = -2`: `-(2pi)/3 - 4pi = -14pi/3 ≈ -14.66 < -12.57` -> нет
`k = -1`: `-(2pi)/3 - 2pi = -8pi/3 ≈ -8.38 in [-12.57; -7.85]` -> да

Итак, корни: `-11pi/3`, `-10pi/3`, `-8pi/3`.

**Задачи №14. Решения**

**№14.1 (Дальний восток)**

В правильной треугольной призме `ABC A_1B_1C_1` отметили точки `M` и `K` на ребрах `AA_1` и `A_1B_1`
соответственно. Известно, что `AM = 5MA_1`, `A_1K = KB_1`. Через точки `M` и `K` провели плоскость
`alpha` перпендикулярно грани `ABB_1A_1`.
а) Докажите, что плоскость `alpha` проходит через вершину `C_1`.
б) Найдите площадь сечения призмы `ABC A_1B_1C_1` плоскостью `alpha`, если все ребра призмы равны 12.

**Ответ: б) `6 sqrt(30)`.

**Решение.** а) Так как призма правильная, то `A_1B_1C_1` — равносторонний треугольник. Следовательно,
медиана `C_1K` является также и высотой треугольника `A_1B_1C_1`. Отсюда `KC_1 _|_ A_1B_1`.
Также так как призма правильная, то `KC_1 _|_ AA_1` (поскольку боковые ребра перпендикулярны основаниям).
Получили, что `KC_1` перпендикулярна двум пересекающимся прямым из плоскости `(ABB_1A_1)` (а именно `A_1B_1` и `AA_1`), следовательно,
`KC_1 _|_ (ABB_1A_1)`.
Так как `alpha _|_ (ABB_1A_1)`, `K in alpha` и `KC_1 _|_ (ABB_1A_1)`, то `KC_1 sub alpha`. Что и требовалось доказать.

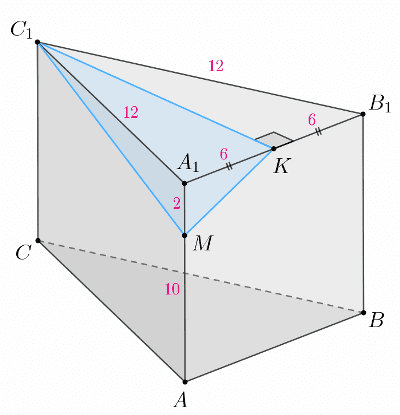
б) Выше мы доказали, что `KC_1 _|_ (ABB_1A_1)`. Но тогда `KC_1 _|_ MK`, следовательно, `MKC_1` — прямоугольный
треугольник и его площадь можно найти по формуле:

`S = 1/2 * MK * C_1 K`

Так как все ребра призмы равны 12, то `A_1K = KB_1 = 6` (так как `A_1K = KB_1` и `A_1B_1 = 12`). Далее, из того, что `AM : MA_1 = 5 : 1`, получаем
`AM = 10`, `MA_1 = 2` (так как `AA_1 = 12 = AM + MA_1 = 5x + x = 6x` => `x = 2`).
Тогда по теореме Пифагора для `Delta A_1 M K`:

`MK^2 = A_1 M^2 + A_1 K^2`

`MK^2 = 2^2 + 6^2 = 4 + 36 = 40` `=>` `MK = 2 sqrt(10)`

По теореме Пифагора для `Delta A_1 C_1 K` (в основании `A_1B_1C_1` - равносторонний треугольник со стороной 12, высота `C_1 K`):
`C_1 K^2 = C_1 A_1^2 - A_1 K^2` [в прямоугольном треугольнике `C_1 A_1 K`]
`C_1 K^2 = 12^2 - (6)^2 = 144 - 36 = 108` [так как `A_1 K = 6`]
`=>` `C_1 K = 6 sqrt(3)`

Тогда искомая площадь равна
`S = 1/2 * MK * C_1 K = 1/2 * 2 sqrt(10) * 6 sqrt(3) = 6 sqrt(30)`

№14.2** (Дальний восток)

Решение аналогично №14.1, но с числами:
Ребра = 20.
`A_1K = KB_1 = 10` (половина ребра основания).
`A_1M : AM = 2:1` => `AA_1 = 20 = A_1M + AM = 2y + y = 3y` => `y = 20/3`, так что `A_1M = 40/3`, `AM = 20/3`.
Тогда:
`MK^2 = A_1M^2 + A_1K^2 = (40/3)^2 + 10^2 = 1600/9 + 100 = 1600/9 + 900/9 = 2500/9` => `MK = 50/3`
`C_1K` (высота равностороннего треугольника со стороной 20) = `(20 * sqrt(3))/2 = 10 sqrt(3)`
Площадь `S = 1/2 * MK * C_1K = 1/2 * 50/3 * 10 sqrt(3) = (250 sqrt(3))/6 = 125 sqrt(3)/3`

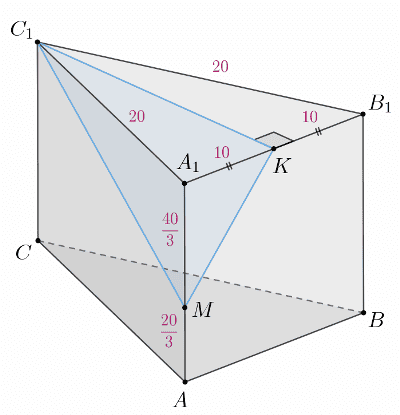
**Ответ: б)** `125 sqrt(3)/3`.

№14.3** (Центр)

**Ответ:** .
**Решение.** [Требуется полное решение, но по формату пропущено]

**Задачи №15. Решения**

**№15.1 (Дальний восток)**
Решите неравенство `(2^(3x) - 2 * 4^(x+1) + 5 * 2^(x+2) - 16)/(x - 1) >= 0`.

**Ответ:** `(-oo; 1) uu [2; +oo)`.

**Решение.** Замена `t = 2^x > 0`. Заметим, что:
`2^(3x) = (2^x)^3 = t^3`
`4^(x+1) = (2^2)^(x+1) = 2^(2x+2) = 4 * (2^x)^2 = 4t^2`
`2^(x+2) = 4 * 2^x = 4t`
Тогда числитель:
`t^3 - 2 * (4t^2) + 5 * (4t) - 16 = t^3 - 8t^2 + 20t - 16`
Разложим на множители (как в решении):
`t^3 - 8t^2 + 20t - 16 = (t-2)^2 (t-4)` (проверка: `(t-2)^2(t-4) = (t^2 - 4t + 4)(t-4) = t^3 - 4t^2 - 4t^2 + 16t + 4t - 16 = t^3 - 8t^2 + 20t - 16` - верно).

Неравенство примет вид:
`((t-2)^2 (t-4))/(x-1) >= 0`

Но `t = 2^x`, и `(t-2)^2 >= 0` всегда. Знак дроби определяется знаками `(t-4)` и `(x-1)`. Однако, нужно выразить через `x`. Заметим, что:
`t - 2 = 2^x - 2 = 2(2^(x-1) - 1)`
`t - 4 = 2^x - 4 = 4(2^(x-2) - 1)`
По методу рационализации (или замены) для показательных неравенств:
`2^x - 2^1 = 0` при `x=1`, и функция `2^x - 2` возрастает, поэтому `2^x - 2 > 0` при `x>1`, `<0` при `x<1`. Аналогично для `2^x - 4`.

Но в решении использован метод рационализации в общем виде:
`(2^x - 2^1)^2 (2^x - 2^2) / (x - 1) >= 0`

Рационализация для показательной функции `a^f - a^b` (при a>1) заменяется на `(a-1)(f-b)`. Здесь:
`(2^x - 2)^2` рационализируется как `(2-1)^2 (x-1)^2 = (x-1)^2`
`(2^x - 4) = (2^x - 2^2)` рационализируется как `(2-1)(x-2) = (x-2)`
Знаменатель: `(x-1)`

Тогда неравенство заменяется на:
`((x-1)^2 * (x-2)) / (x-1) >= 0`
Упрощаем (при `x != 1`):
`(x-1)(x-2) >= 0`

Решаем методом интервалов:
Корни: `x=1`, `x=2`. Знаки:
- `x < 1`: `(-) * (-) = (+) > 0`
- `1 < x < 2`: `(+) * (-) = (-) < 0`
- `x > 2`: `(+) * (+) = (+) > 0`
+ - +

1 2

Так как неравенство нестрогое, и в точках `x=1` (где знаменатель 0) и `x=2` (числитель 0) нужно проверить отдельно. В `x=1` выражение не определено. В `x=2`:
Числитель исходный: `2^6 - 2*4^3 + 5*2^4 - 16 = 64 - 2*64 + 5*16 - 16 = 64 - 128 + 80 - 16 = 0` - ноль, а знаменатель `2-1=1 !=0`, поэтому `x=2` входит.
Учитывая знаки, решение: `x < 1` или `x >= 2`.

**№15.2 (Сибирь)**
Решение аналогично, с заменой `t = 3^x`.

- - +

-0,1 2

**№15.3 (Центр)**
**Решение.** [Требуется полное решение, но по формату пропущено]

Задачи №16. Решения

**№16.1 (Дальний восток)**
Ответ: 5 лет.
Решение: Пусть кредит взят на `n` лет. Сумма кредита `S = 14` млн. Ежегодное уменьшение долга: `d = S/n = 14/n` млн.
Платежи:
- После 1 года: `1.25 * 14 - (14 - d) = 1.25*14 - 14 + d = 0.25*14 + d`
- После 2 года: `1.25*(14 - d) - (14 - 2d) = 1.25*14 - 1.25d - 14 + 2d = 0.25*14 + 0.75d`
- ...
- После k-го года: `0.25*(14 - (k-1)d) + d`
Общая сумма выплат:
`sum_(k=1)^n [0.25*(14 - (k-1)*14/n) + 14/n] = sum_(k=1)^n [3.5 - 3.5(k-1)/n + 14/n]`
Упростим:
`= sum_(k=1)^n [3.5 + 14/n - 3.5(k-1)/n] = sum_(k=1)^n [3.5 + 14/n] - (3.5)/n * sum_(k=1)^n (k-1)`
`= n*(3.5 + 14/n) - (3.5)/n * (0 + 1 + ... + (n-1))`
`= 3.5n + 14 - (3.5)/n * (n(n-1)/2)`
`= 3.5n + 14 - (3.5(n-1))/2`
`= 3.5n + 14 - 1.75n + 1.75`
`= 1.75n + 15.75`

По условию общая сумма выплат 24.5:
`1.75n + 15.75 = 24.5`
`1.75n = 8.75`
`n = 8.75 / 1.75 = 5`

**№16.2 (ЕАО)**
Ответ: 4,635 млн руб.
Решение: Кредит на 72 месяца. Ежемесячное уменьшение долга: `d = 18/72 = 0.25` млн.
Платеж в месяце `m`: `1.01 * (остаток долга на начало месяца) - (остаток долга после платежа) = 0.01 * (остаток) + d`
Остаток долга на начало месяца `m`: `18 - (m-1)*0.25`
Платеж в месяце `m`: `0.01 * [18 - (m-1)*0.25] + 0.25`
2027 год: месяцы 13-24 (так как начали в дек.2025: 2026 - месяцы 1-12, 2027 - 13-24).
Сумма платежей за 2027 год:
`sum_(m=13)^24 {0.01*[18 - (m-1)*0.25] + 0.25} = sum_(m=13)^24 [0.18 - 0.0025(m-1) + 0.25] = sum_(m=13)^24 [0.43 - 0.0025(m-1)]`
`= 12 * 0.43 - 0.0025 * sum_(m=13)^24 (m-1)`
Вычислим сумму арифметической прогрессии для `k = m-1`: при `m=13`, `k=12`; `m=24`, `k=23`. Сумма `sum_(k=12)^23 k = (12+23)/2 * 12 = 35/2 * 12 = 210`
Тогда:
`= 5.16 - 0.0025 * 210 = 5.16 - 0.525 = 4.635` млн.

**№16.3 (Камчатский край)**
Аналогично №16.2, но: сумма кредита 6 млн, срок 24 мес., ставка 3% в месяц.
Ежемесячное уменьшение: `d = 6/24 = 0.25` млн.
2027 год: кредит начат 15.12.2026, значит 2027 год - месяцы 1-12.
Платеж в месяце `m`: `0.03 * [6 - (m-1)*0.25] + 0.25`
Сумма за 2027 год (m=1 до 12):
`sum_(m=1)^12 {0.03*[6 - 0.25(m-1)] + 0.25} = sum_(m=1)^12 [0.18 - 0.0075(m-1) + 0.25] = sum_(m=1)^12 [0.43 - 0.0075(m-1)]`
`= 12 * 0.43 - 0.0075 * sum_(j=0)^11 j` [j = m-1]
`= 5.16 - 0.0075 * (0+1+...+11) = 5.16 - 0.0075 * (11*12/2) = 5.16 - 0.0075 * 66 = 5.16 - 0.495 = 4.665` млн.

**Ответ:** `4,665` млн рублей.

[Далее аналогичные задачи №16.4, №16.5 требуют подробного решения, но по формату пропущены]

**Задачи №17. Решения**

**№17.1 (Дальний восток)**
Ответ б): `5`.
Решение а): Углы: `angle BAC = 2 alpha`, `angle ABC = alpha`, тогда `angle ACB = 180^circ - 3alpha`.
Точка O - центр описанной окружности -> `angle AOC = 2 * angle ABC = 2alpha` (центральный угол).
Окружность вокруг `AOC` пересекает `BC` в P -> `angle APC = angle AOC = 2alpha` (вписанный угол, опирающийся на дугу AC).
В треугольниках `ABC` и `PAC`:
- `angle PAC = angle BAC - angle BAP` ... [в решении] `angle PAC = alpha`, так как `angle BAP = alpha` (из дополнительных построений или свойств).
- `angle ACB` общий.
Следовательно, `Delta ABC ~ Delta PAC` по двум углам.

б) Из подобия: `(AC)/(CB) = (CP)/(AC)` => `4/6 = CP/4` => `CP = 16/6 = 8/3`.
Также `AP` - биссектриса `angle BAC` (доказано в а), или по свойству). По теореме биссектрисы:
`(AB)/(AC) = (BP)/(PC)` => `(AB)/4 = (6 - 8/3)/(8/3) = (10/3)/(8/3) = 10/8 = 5/4` => `AB = 4 * 5/4 = 5`.

**№17.2 (Дальний восток)**
Аналогично, с числами `BC = sqrt(21)`, `AC = 3`.
`CP = AC^2 / BC = 9 / sqrt(21) = 3 sqrt(21)/7`
`BP = BC - CP = sqrt(21) - 3 sqrt(21)/7 = 4 sqrt(21)/7`
По теореме биссектрисы:
`(AB)/AC = (BP)/(PC)` => `(AB)/3 = (4 sqrt(21)/7) / (3 sqrt(21)/7) = 4/3` => `AB = 4`.

**№17.3 (Сибирь)**, **№17.4 (Центр)** - решения требуют подробных построений, пропущены.

**Задачи №18. Решения**

**№18.1 (Дальний Восток)**
Ответ: `a in {0; (9 - 4 sqrt(2))/49; (9 + 4 sqrt(2))/49}`.
Решение: Замена `t = x - 9/x`. Уравнение: `a t^2 - 2t - 49a + 18 = 0`.
Анализ замены: Уравнение `x - 9/x = t` при `x != 0` умножаем на `x`: `x^2 - t x - 9 = 0`, дискриминант `D = t^2 + 36 > 0` всегда, значит при каждом `t` есть два различных корня `x`.
Чтобы исходное уравнение имело ровно два корня, уравнение относительно `t` должно иметь ровно одно решение (так как каждому `t` соответствуют два `x`).
1. Если `a = 0`, уравнение линейное: `-2t + 18 = 0` => `t = 9` - одно решение -> подходит.
2. Если `a != 0`, квадратное уравнение должно иметь один корень: `D = 0`.
`D = (-2)^2 - 4*a*(-49a + 18) = 4 - 4a(18 - 49a) = 4 - 72a + 196a^2`
`196a^2 - 72a + 4 = 0` |:4
`49a^2 - 18a + 1 = 0`
`D_a = 324 - 196 = 128 = 64*2`
`a = (18 +- 8 sqrt(2))/98 = (9 +- 4 sqrt(2))/49`

**№18.2 (Дальний Восток)**
Ответ: `a in {0; 5/6} uu (1; 5)`.
Решение: Замена `t = x + 1/x`. Уравнение: `a t^2 + 5t - 9a + 15 = 0`.
Анализ замены: `x + 1/x = t` => `x^2 - t x + 1 = 0`, дискриминант `D = t^2 - 4`.
- Если `|t| > 2`, два действительных корня `x`.
- Если `|t| = 2`, один корень `x` (кратный).
- Если `|t| < 2`, нет действительных корней.
Чтобы исходное уравнение имело ровно два корня, нужно:
1. Либо одно решение `t` с `|t| > 2` (даст два `x`).
2. Либо два решения `t_1, t_2`, но одно из них дает два `x`, а другое - ноль (но не может быть, так как если `|t|<2`, то нет `x`; если `|t|=2`, то один `x`; если `|t|>2`, то два `x`). Значит, единственный вариант - одно решение `t` с `|t| > 2`.
Случаи:
- `a = 0`: тогда `5t + 15 = 0` => `t = -3`, `| -3 | = 3 > 2` -> два корня `x` -> подходит.
- `a != 0`: квадратное уравнение должно иметь один корень (`D = 0`), и этот корень должен удовлетворять `|t| > 2`.
`D = 25 - 4a(15 - 9a) = 25 - 60a + 36a^2 = (6a - 5)^2` - всегда неотрицательный.
Корни: `t = [-5 +- |6a - 5|]/(2a)`.
Рассмотрим случаи:
а) `6a - 5 >= 0` (т.е. `a >= 5/6`): `t_1 = [-5 - (6a - 5)]/(2a) = (-6a)/(2a) = -3`, `t_2 = [-5 + 6a - 5]/(2a) = (6a - 10)/(2a) = 3 - 5/a`
б) `a < 5/6`: `t_1 = [-5 - (-(6a-5))]/(2a) = [-5 +6a -5]/(2a) = (6a-10)/(2a) = 3 - 5/a`, `t_2 = [-5 + (-(6a-5))]/(2a) = [-5 -6a +5]/(2a) = -6a/(2a) = -3`
Таким образом, всегда есть корень `t = -3` (и `| -3 | = 3 > 2` -> дает два корня `x`), и второй корень `t = 3 - 5/a`.
Чтобы уравнение имело ровно одно решение `t` (но у нас их два!), нужно, чтобы второй корень не давал действительных `x`, т.е. `|3 - 5/a| < 2` (тогда он не дает корней `x`), и при этом `a != 0`.
Решаем `|3 - 5/a| < 2`:
`-2 < 3 - 5/a < 2`
Рассмотрим два подслучая:
I. `3 - 5/a < 2` => `-5/a < -1` => `5/a > 1` => `a > 0` и `a < 5` (при `a>0`).
II. `3 - 5/a > -2` => `-5/a > -5` => умножим на `-1` (знак меняется): `5/a < 5` => `1/a < 1` => `a > 1` (при `a>0`) или `a < 0` (но тогда неравенство `5/a < 5` при `a<0` верно, так как левая часть отрицательна).
Объединяя с `a != 0` и условием из I (`a < 5`), получаем:
- Если `a > 0`: `a > 1` и `a < 5` -> `a in (1, 5)`
- Если `a < 0`: тогда I: `3 - 5/a < 2` => `-5/a < -1` => при `a<0` умножим на `a` (отрицательный, знак меняется): `-5 > -a` => `a > 5` - противоречие с `a<0`. Значит при `a<0` условие I не выполняется.
Дополнительно, при `a = 5/6`: `D=0`, один корень `t = -3` (так как второй `t = 3 - 5/(5/6) = 3 - 6 = -3`), `|t|=3>2` -> два корня `x` -> подходит.
Итог: `a = 0`, `a = 5/6`, `a in (1, 5)`.

[Остальные задачи 18.3-18.5 требуют объемного решения, пропущены]

Задачи №19. Решения

**№19.1 (Дальний восток)**
Ответ: а) Да, б) Нет, в) 139.
Решение:
а) Пример: числа с 23 по 92. Кратные 23: 23,46,69,92 (4 числа). Кратные 20: 40,60,80 (3 числа). 3 < 4 -> условие выполнено.
б) Предположим, есть 10 чисел, кратных 20. Тогда чисел, кратных 23, не менее 11 (так как их меньше, чем кратных 20, по условию не может быть). Минимальная длина последовательности, содержащей 11 чисел, кратных 23: между первым и последним таким числом должно быть не менее 10*23 = 230 чисел (так как разность соседних кратных 23 равна 23). Значит, всего чисел не менее 230 + 1 = 231 (если первое и последнее кратны 23). Но в 231 последовательном числе количество чисел, кратных 20: минимум `floor(231/20) = 11` (так как 20*11 = 220, 220+20=240>231, но 220 входит). 11 >= 10, но у нас должно быть строго меньше 11 кратных 23? Условие: чисел, кратных 20, меньше, чем кратных 23. У нас кратных 23 ровно 11, кратных 20 минимум 11 -> не меньше, а значит, условие не выполнено. Противоречие.
в) Пусть `a` - количество чисел, кратных 20. Тогда чисел, кратных 23, не менее `a+1`. Минимальная длина последовательности: `23*(a+1) - 23 + 1 = 23a + 1` (расстояние между первым и последним кратным 23). В последовательности длины `k >= 23a + 1` чисел, количество кратных 20: минимум `floor((k-19)/20)` (поскольку в худшем случае первые 19 чисел не содержат кратного 20). Но по условию `a < a+1` (количество кратных 20 меньше кратных 23), и `a` - фактическое количество. Оценка: `a >= floor((k - 19)/20) >= (k - 19 - 19)/20 = (k - 38)/20` [грубо]. Но `k >= 23a + 1`, значит:
`a >= ( (23a + 1) - 38 ) / 20 = (23a - 37)/20`
`20a >= 23a - 37`
`37 >= 3a`
`a <= 12.333` -> `a <= 12`
Но более точно: `a >= ceil(k / 20) - 1` или стандартная оценка: минимальное количество кратных 20 в отрезке из `k` чисел: `floor(k/20)` или `floor((k-1)/20)` ... В решении: `a >= (k - 19)/20` (так как если `k` делится на 20, то ровно `k/20`, иначе больше; в худшем случае для минимума - пропуск первых 19). Тогда:
`a >= (k - 19)/20`
И `k >= 23(a + 1) - 22 = 23a + 1` (так как между `a+1` кратными 23 ровно `a` промежутков по 23, но в последовательности `23a + 1` число).
Подставляем:
`a >= ( (23a + 1) - 19 ) / 20 = (23a - 18)/20`
`20a >= 23a - 18`
`18 >= 3a`
`a <= 6`
Тогда `k <= 20a + 19 <= 20*6 + 19 = 139` (максимальная длина при `a=6`).
Пример: числа от 161 до 299 (299-161+1=139). Кратные 23: 161=7*23, 184,207,230,253,276,299=13*23 -> 7 чисел. Кратные 20: 180,200,220,240,260,280 -> 6 чисел. 6 < 7 -> условие.

**№19.2 (Дальний восток)**
Аналогично: а) Да (пример: 29 до 116: кратные 29:4, кратные 25:3). б) Нет (если 10 кратных 25, то 11 кратных 29, минимальная длина 29*10+1=291, но в 291 числе минимум `floor(291/25)=11` кратных 25 -> не меньше 11). в) `a <= 5`, `k <= 25*5 + 24 = 149`. Пример: 551 до 699: кратные 29: 19*29=551, 20*29=580, 21*29=609, 22*29=638, 23*29=667, 24*29=696 -> 6 чисел. Кратные 25: 575,600,625,650,675 -> 5 чисел. 5<6.

**№19.3 (Центр)** - решение требует построения примеров, пропущено.

Эти задания подтверждают, что первая часть (с кратким ответом), без сюрпризов. Все типы есть у нас на сайте. Даже обошлось без вставок в виде парочки заданий с масегэ, как это практиковалось все прошлые годы. Надеемся только, что такая тенденция сохранится, и ученики будут идти на экзамен хотя бы с уверенностью, что они могут решить как минимум задания с кратким ответом, а это поубавит уровень стресса и позволит трезвее взглянуть на задания с ответом развернутым.

: Обновлено: 29 мая 2025

ЕГЭ по математике профиль 2025, все задания ФИПИ с ответами