Все треугольники в пятнадцатом задании по геометрии вполне самостоятельные, без вписанных/описанных окружностей (которые уже из задания 16). Все типы заданий представлены ниже, и это только типы, к каждому типу может быть десяточек вариантов ФИПИ с другими числами.
Типы заданий линейки 15 по ФИПИ
Биссектриса, медиана
1. В треугольнике ABC известно, что ∠BAC=82°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
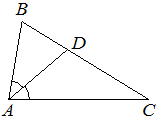
Решение:
Биссектриса делит угол пополам, значит
∠BAD = 82 / 2 = 41°
Ответ: 41
2. В треугольнике ABC известно, что АС =18, BM – медиана, BM=14. Найдите АM.
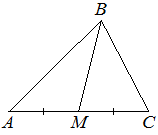
Решение:
Медиана делит сторону пополам, значит
AM = АС/2 = 18/2 = 9
Ответ: 9
Задания про середины сторон треугольника >>
2026 3. В треугольнике АВС проведена биссектриса АК. Найдите градусную меру угла В, если ∠С=12° и АК=СК.
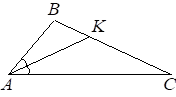
Решение:
Треугольник АКС равнобедренный ⇒ углы при основании равны:
∠С=∠КАС=12°
Биссектриса делит угол пополам ⇒
∠ВАС=12°*2=24°
Сумма углов треугольника равна 180° ⇒
∠В=180-12-24=144°
Ответ: 144
2026 4. В треугольнике АВС проведена медиана ВМ. Найдите градусную меру угла А, если ∠С=65° и ВМ=АМ=МС.
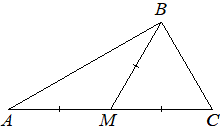
Решение:
∠С=∠СВМ=65° (углы у основания равнобедренного треугольника равны)
Сумма углов треугольника = 180° ⇒
в △ВМС ∠ВМС=180-65*2=50°
в △ВМА ∠ВМА=180-50=130°
∠А=(180-130):2=25°
Ответ: 25
Сумма углов треугольника
5. В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
Решение:
Сумма углов треугольника равна 180°. Следовательно, чтобы найти третий угол треугольника, нужно сложить два известных угла и вычесть их сумму из 180°
180° − (72° + 42°) = 66°
Ответ: 66
6. В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внутренний угол С треугольника ABC и внешний угол при вершине C смежные, а значит их сумма равна 180°. Тогда, внешний угол при вершине C равен
180°-133°=47°
Ответ: 47
![]() 7 2025. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ABC. Ответ дайте в градусах.
7 2025. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ABC. Ответ дайте в градусах.
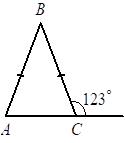
Решение:
Угол ACB и внешний дают в сумме 180° ⇒ ∠ACB = 180-123=57°
Треугольник равнобедренный, значит углы при основании равны ⇒ ∠BAC=∠ACB=57°.
Сумма углов треугольника всегда равна 180°
∠ABC=180-57*2=66°
Ответ: 66
Номер: C24747
8. В треугольнике ABC известно, что AB=BC, ∠ABС =124°. Найдите угол BCA. Ответ дайте в градусах.
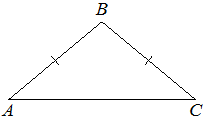
Решение:
Сумма углов треугольника равна 180°.
Треугольник равнобедренный, значит углы при основании равны.
∠ВСА =∠ВАС = (180° - 124°) / 2 = 28°
Ответ: 28
9. Один из острых углов прямоугольного треугольника равен 53°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:
Сумма углов треугольника равна 180°.
Прямой угол равен 90°.
Следовательно, чтобы найти другой острый угол треугольника, нужно из 180° отнять 90° и отнять известный угол.
180° − 90° − 53° = 37°
Ответ: 37
10. В остроугольном треугольнике ABC проведена высота BH, ∠BAC=64°. Найдите угол ABH. Ответ дайте в градусах.
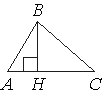
Решение:
ABH - прямоугольный треугольник, так как BH - высота.
По теореме о сумме углов треугольника
∠ABH+∠AHB+∠BAH = 180°
∠ABH = 180° - ∠AHB - ∠BAH
∠BAH - это ∠BAC, он равен 64°
∠AHB = 90°
∠ABH = 180 - 90 - 64 = 26°
Ответ: 26
![]() В треугольнике ABC угол C равен 90°, M – середина стороны AB, AB=36, BC=20. Найдите CM.
В треугольнике ABC угол C равен 90°, M – середина стороны AB, AB=36, BC=20. Найдите CM.
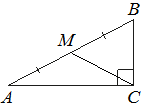
Решение:
CM — медиана, а медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, значит,
CM = AB/2 = 36/2 = 18
Ответ: 18
Площадь треугольника
11. Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 6 * 7 = 21
Ответ: 21
12. Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
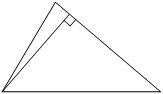
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 24 * 19 = 228
Ответ: 228
![]() На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10 . Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10 . Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.

Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 6 + 10 = 16
SВСD = 48 * 10 / 16 = 30
Ответ: 30
Еще задания про площадь треугольника >>
Подобные треугольники
13. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
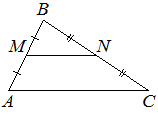
Решение:
Поскольку отрезок MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
МN = АС/2 = 72/2 = 36
Ответ: 36
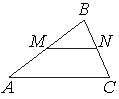
![]() Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 18/24 * 28 = 21, тогда
AM = AB − BM = 28 - 21 = 7
Ответ: 7
![]() Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.

Решение:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$, поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (14/21)2 * 27 = 12
Ответ: 12
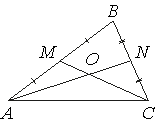
![]() Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Решение:
Отрезки AN и CM — медианы. Медианы в треугольнике при пересечении делятся в отношении 2:1 (первое свойство медианы), считая от вершины:
AO = 2
ON 1
Всего частей 3, следовательно,
AO = 2 ⇒
AN 3
AO = 2/3 * AN = 2/3 * 24 = 16
Ответ: 16
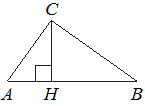
![]() На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Решение:
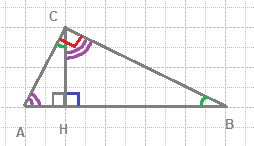
Рассмотрим треугольники ACH и BCH.
Докажем, что это подобные треугольники.
∠AHC=∠BHC=90° (так как CH - высота).
По теореме о сумме углов треугольника:
∠CAH+∠AHC+∠HCA=180°
∠CAH+90°+∠HCA=180°
∠CAH+∠HCA=90°
∠CAH=90°-∠HCA
Заметим, что ∠BCH=90°-∠HCA (так как ∠АСВ прямой)
Получается, что ∠CAH=∠BCH
Тогда, по первому признаку подобия, данные треугольники подобны,
значит, можем записать пропорцию:
AH = CH
CH BH
Чтобы не ошибиться в пропорции, мысленно переверните правый треугольник против часовой стрелки, чтобы он "стоял" на стороне СН.
CH2 = AH*BH
CH2 = 2*18
CH2 = 36
CH =√36
CH =6
Ответ: 6
Теорема Пифагора
14. Катеты прямоугольного треугольника равны 10 и 24. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 102 + 242 = 100 + 576 = 676
гипотенуза = √676 = 26
Ответ: 26
15. В прямоугольном треугольнике катет и гипотенуза равны 20 и 25 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 252 - 202 = √ 625 - 400 = √ 225 = 15
Ответ: 15
![]() Высота равностороннего треугольника равна 9√3. Найдите его периметр.
Высота равностороннего треугольника равна 9√3. Найдите его периметр.
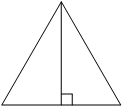
Решение:
В равностороннем треугольнике высота является медианой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
а = 9√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 9√3 = 2 * 9 = 18
18*3=54
Ответ: 54
16. Сторона равностороннего треугольника равна 16√3. Найдите медиану этого треугольника.
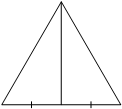
Решение:
Поскольку проведена медиана, а медиана в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. 
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
с = 16√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 16√ 3 = 16 * 3/2 = 24
Ответ: 24
17. В треугольнике ABC известно, что AC = 20, BC = 21, угол C равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение:
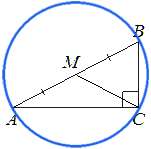 Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.
AB = √ (AC² + BC²) = √ (20² + 21²) = √ (400 + 441) = √ 841 = 29
Найдем радиус.
R = 1/2 * AB = 1/2 * 29 = 29/2 = 14,5
Ответ: 14,5
Синус, косинус, тангенс острого угла
18. В треугольнике ABC угол C равен 90°, AC = 9, AB = 25. Найдите sinB.

Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
19. В треугольнике ABC угол C равен 90°, BC = 14, AB = 20. Найдите cosB.

Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
20. В треугольнике ABC угол C равен 90°, BC = 9, AC = 27. Найдите tgB.

Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
21. В треугольнике ABC угол C равен 90°, cosB = 3/8, AB = 64. Найдите BC.

Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24
Ответ: 24
22. В треугольнике ABC угол C равен 90°, sinB = 3/7, AB = 21. Найдите AC.

Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9
Ответ: 9
23. В треугольнике ABC угол C равен 90°, tgB = 5/9, BC = 27. Найдите AC.

Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15
Ответ: 15
24. Синус острого угла A треугольника ABC равен √15/4. Найдите cosA.

Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 - sin2A =1 - (√15/4)2 = 1 - 15/16 = 1-0,9375 = 0,0625
cosA = 0,25
Ответ: 0,25
25. Косинус острого угла A треугольника ABC равен √21/5. Найдите sinA.

Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 - cos2A =1 - (√21/5)2 = 1 - 21/25 = 1-0,84 = 0,16
sinA = 0,4
Ответ: 0,4
Теорема о площади треугольника
26. В треугольнике ABC известно, что AB = 12, BC = 10, sin ∠ABC = 8/15. Найдите площадь треугольника ABC.
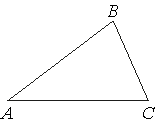
Решение:
S = 1/2аb • sinγ = 1/2*12*10*8/15=32
Ответ: 32
Теорема синусов и теорема косинусов
![]() В треугольнике ABC угол A равен 45°, угол B равен 60°, BC = 4√6. Найдите AC.
В треугольнике ABC угол A равен 45°, угол B равен 60°, BC = 4√6. Найдите AC.

Решение:
По теореме синусов:
$\frac{АС}{\sin B}=\frac{BC}{\sin A}$
АС = ВС/sinA * sinB
$АС=\frac{4\sqrt6}{\displaystyle\frac{\sqrt2}2}\ast\frac{\sqrt3}2=\frac{4\cancel{\sqrt6}^{(\sqrt{3)}}\ast\cancel2\ast\sqrt3}{\cancel{\sqrt2\ast2}}=4\ast3=12$
Ответ: 12
Подобные задания с другими числами >>
![]() В треугольнике ABC известно, что AB=2, BC = 3, AC = 4. Найдите cos ∠ABC.
В треугольнике ABC известно, что AB=2, BC = 3, AC = 4. Найдите cos ∠ABC.

Решение:
а2 = b2 + с2 - 2bс • cosα
2bс • cosα = b2 + с2 - а2
$\cos\alpha=\frac{b^2+с^2-а^2}{2bс}$
$\cos\alpha=\frac{2^2+3^2-4^2}{2\ast 2\ast 3}$= -3/12 = -0,25
Ответ: -0,25

