Мы собрали все прототипы заданий с кратким ответом по стереометрии, какие могут вам попасться на реальном ЕГЭ по профильной математике.
Объём многогранника
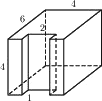
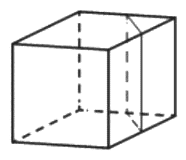
Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).

Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 3*2*3-1*1*3=15
Ответ: 15
Номер: 79A288
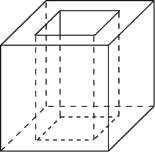
Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).

Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 5*3*1-1*1*3=12
Ответ: 12
Номер: 0630DF
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
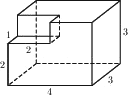
Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 4*3*3-1*2*1=34
Ответ: 34
mathege
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
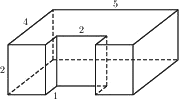
Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 4*5*2-2*2*1=36
Ответ: 36
mathege
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
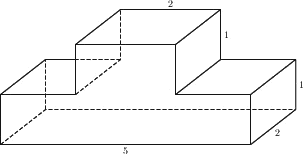
Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 5*2*1+2*2*1=14
Ответ: 14
mathege
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
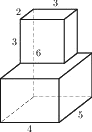
Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 2*3*3+4*5*3=78
Ответ: 78
mathege
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
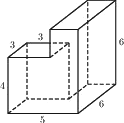
Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 3*3*4+2*6*6=108
Ответ: 108
mathege
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
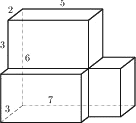
Решение:
V параллелепипеда = ab*h (произведению его граней)
V = 3*2*5+2*2*3+3*3*5=87
Ответ: 87
mathege
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
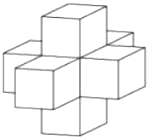
Решение:
7 кубов, значит и объем равен 7 кубам.
Ответ: 7
mathege
Площадь поверхности многогранника
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы – прямые).

Решение:
Площадь прямоугольника равна произведению двух сторон.
(6-2)/2=2 размерность неизвестных сторон
Sпов. = 2*4*7+(2*2+6*2)*2+6*4=56+32+24=112
Ответ: 112
Номер: 0CD226
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
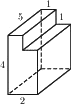
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 4*5*2+2*5*2+(4*2-1)*2=40+20+14=74
Ответ: 74
mathege
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
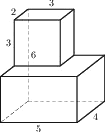
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 4*5*2+3*4*2+3*3*2+3*2*2+5*3*2=40+24+18+12+30=124
Ответ: 124
mathege
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
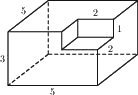
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 5*5*2+5*3*4 = 110
Ответ: 110
ЕГЭ 2016
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
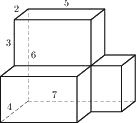
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 24+24+18+18+36+36=156
Ответ: 156
mathege
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 36+36+21+21+24+24=162
Ответ: 162
mathege
Найдите площадь поверхности пространственного креста, изображённого на рисунке и составленного из единичных кубов.

Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 5+5+5+5+5+5=30
Ответ: 30
mathege
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
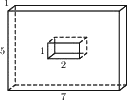
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 5+5+7+7+33+33+2+2+1+1=96
Ответ: 96
mathege
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 24+24+16+16+22+22+4+4=132
Ответ: 132
mathege
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Решение:
Площадь прямоугольника равна произведению двух сторон.
Sпов. = 1+1+1+1+0,75+0,75+0,5+0,5+0,5+0,5=7,5
Ответ: 7,5
mathege
Углы многогранника
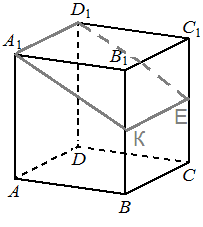
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла 𝐶3𝐷3𝐵3
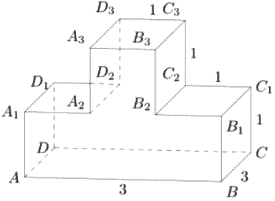
Решение:
`tg∠(C_3D_3B_3) = (B_3C_3)/(D_3C_3)=3/1=3`
Ответ: 3
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла 𝐵2𝐴2𝐶2
Решение:
`tg∠(B_2A_2C_2) = (B_2C_2)/(A_2B_2)=2/1=2`
Ответ: 2
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла 𝐶2𝐶3𝐵2

Решение:
`tg∠(C_2C_3B_3) = (B_2C_2)/(C_2C_3)=3/1=3`
Ответ: 3
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла 𝐴𝐵𝐵3

Решение:
`tg∠(ABB_3) = (B_3K)/(BK)=2/1=2`
Ответ: 2
mathege
Расстояние между вершинами многогранника
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами 𝐴 и 𝐶2.

Решение:
1) Δ`A_2D_2C_2` `A_2C_2=sqrt(2^2+1^2) =sqrt5`
2) Δ`A A_2C_2` `AC_2=sqrt(2^2+(sqrt5)^2) =3`
Ответ: 3
mathege
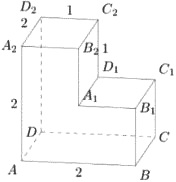
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами 𝐵 и 𝐷2.

Решение:
1) `D_2K=1`
`CK=1+1=2`
2) `ΔBCK` `BK = sqrt(3^2+2^2) = sqrt13`
3) `ΔBKD_2` `BD_2 = sqrt((sqrt13)^2+1) = sqrt14`
4) `(BD_2)^2 = (sqrt14)^2=14`
Ответ: 14
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами 𝐵2 и 𝐷3.

Решение:
1)`ΔB_3C_3D_3` `B_3D_3 = sqrt(3^2+1^2) = sqrt10`
2)`ΔB_2B_3D_3` `B_2D_3 = sqrt((sqrt10)^2+1^2) = sqrt11`
3) `(B_2D_3)^2 = (sqrt11)^2 = sqrt11`
Ответ: 11
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами 𝐴 и 𝐶3.

Решение:
Продолжим прямую C3C2 вниз до пересечения с основанием, там отметим точку K.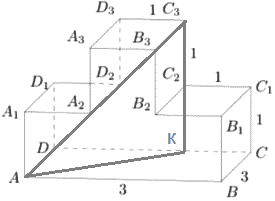
1)`С_3K=1+1=2`
`DK=3-1=2`
2) `ΔADK` `АК = sqrt(3^2+2^2) = sqrt13`
3) `ΔAKС_3` `АС_3 = sqrt((sqrt13)^2+2^2) = sqrt17`
4) `(АС_3)^2 = (sqrt17)^2 = 17`
Ответ: 17
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами 𝐷 и 𝐶2.
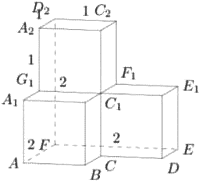
Решение:
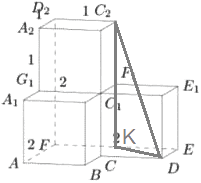
1)`С_2K=2`
`KE=2-1=1`
2) `ΔDKE` `DK = sqrt(1^2+1^2) = sqrt2`
3) `ΔKDC_2` `C_2D = sqrt(2^2+(sqrt2)^2) = sqrt6`
4) `(С_2D)^2=(sqrt6)^2 = 6`
Ответ: 6
mathege
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами 𝐵1 и 𝐷2.

Решение:
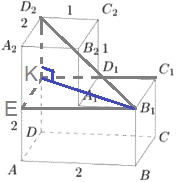
1)`D_2K=C_2D_1=1`
2) `ΔB_1KE` `B_1K = sqrt(2^2+2^2) = sqrt8`
3) `ΔB_1KD_2` `B_1D_2 = sqrt(1^2+(sqrt8)^2) = 3`
Ответ: 3
mathege
Куб
В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 найдите угол между прямыми AC и BB1. Ответ дайте в градусах.

Решение:
Прямые AC и BB1 не пересекаются. Но С1С||BB1 , значит можем перенести BB1 параллельным переносом на прямую СС1.
Угол ACC1 = 90°, так как это угол между прямой, лежащей в основании куба и гранью боковой стороны.
Ответ: 90
Номер: 09E9B4
В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 найдите угол между прямыми BA1 и D1C1. Ответ дайте в градусах.

Решение:
D1C1||A1B1, значит можно перенести D1C1 в A1B1 параллельным переносом.
Проведем диагональ A1B. Получим треугольник A1BB1 равнобедренный и прямоугольный.
Угол BA1B1=(180-90)/2=45°.
Ответ: 45
Номер: 0A2A44
В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 найдите угол между прямыми A1D и B1D1. Ответ дайте в градусах.

Решение:
Получается, надо найти угол BDA1.
Если провести диагонали A1D, DB, A1B, то они все равны и получается равносторонний треугольник. А в равностороннем треугольнике углы равны 180/3=60°.
Ответ: 60
Номер: 21B915
В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 найдите угол между прямыми CD1 и AD. Ответ дайте в градусах.

Решение:
Найти надо BCD1, так как AD||CB.
Если проведем СD1, то получим прямоугольник A1BСD1. В нем углы равны 90°.
Ответ: 90
Номер: DC1005
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 1,5. Найдите объём куба.
Решение:
Отношение площадей `S_(больш.Δ)/S_(мал.Δ) = k^2`
1) Рассмотрим ABCD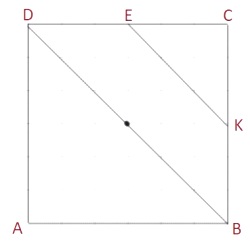
ΔCEK∼ΔBCD
`k=2`
`S_(BCD)/S_(CEK) = 2^2`
То есть в ΔBDC войдет 4 треугольника KEC, а в четырехугольник - 8 треугольников KEC.
2) `V_(куба) = 8*V_(приз) = 8*1,5=12`
Ответ: 12
Номер: 4437
Объём куба равен 80. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Решение:
Отношение площадей `S_(больш.Δ)/S_(мал.Δ) = k^2`
1) Рассмотрим ABCD
ΔCEK∼ΔBCD
`k=2`
`S_(BCD)/S_(CEK) = 2^2`
То есть в ΔBDC войдет 4 треугольника KEC, а в четырехугольник - 8 треугольников KEC.
`V_(приз)=1/8V_(куба)=1/8*80=10`
Ответ: 10
Номер: F51D9A
Диагональ куба равна √12. Найдите его объем.
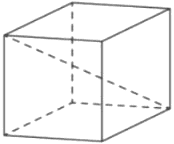
Решение:
Диагональ куба `d = sqrt3 a`
Объем куба `V=a^3`
1 способ
1) `sqrt12=sqrt3*a`
`a=sqrt4=2`
2) `V=2^3=8`
2 способ
1) `BC=sqrt(a^2+a^2) = sqrt(2a^2) = sqrt2 * a`
2) `CD = sqrt(a^2+sqrt(2a)^2) = sqrt(3a^2) =sqrt3 * a`
3) `sqrt12 = sqrt3*a`
`a=2`
4) `V =2^3=8`
Ответ: 8
ЕГЭ 2014
Объем куба равен 8. Найдите площадь его поверхности.
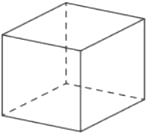
Решение:
Объем куба `V=a^3`
Площадь поверхности `S = 6*a^2`
1) `V=8=a^2`
`a=2`
2) `S = 6*2^2 = 24`
Ответ: 24
mathege
Площадь поверхности куба равна 24. Найдите его объём.

Решение:
Объем куба `V=a^3`
Площадь поверхности `S = 6*a^2`
1) `S_(пов.) = 24 = 6a^2`
`a = 2`
2) `V=2^3=8`
Ответ: 8
mathege
Площадь поверхности куба равна 18. Найдите его диагональ.

Решение:
Объем куба `V=a^3`
Площадь поверхности `S = 6*a^2`
1) `S_(пов.)= 6a^2=18`
`a = sqrt3`
2) `AB=sqrt(sqrt3^2+sqrt3^2)=sqrt6`
3) `BD=sqrt(sqrt6^2+sqrt3^2)=sqrt9=3`
Ответ: 3
mathege
Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?

Решение:
Объем куба `V=a^2`
1)`V_(мал)=a^3`
2) `V_(бол)=(3a)^3=27a^3`
в 27 раз
Ответ: 27
mathege
Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза?

Решение:
Площадь поверхности `S = 6*a^2`
1) `S_(мал)= 6*a^2`
2) `S_(бол)= 6*(3a)^2 = 54a^2`
`54:6=9` раз
Ответ: 9
mathege
Объём куба равен 24√3. Найдите его диагональ.

Решение:
Диагональ куба `d = sqrt3 a`
Объем куба `V=a^3`
Обозначим диагональ куба DC, а диагональ основания BC.
1) `V = 24sqrt3 = a^3`
`8*3sqrt3=a^3`
`2^3*sqrt3^2*sqrt3^1=a^3`
`2^3*sqrt3^3=a^3`
`a=2sqrt3`
2) `BC =sqrt((2sqrt3)^2+(2sqrt3)^2) =sqrt24`
3) `DC = sqrt(sqrt24^2+(2sqrt3)^2)=sqrt36=6`
Ответ: 6
mathege
Если каждое ребро увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Решение:
Площадь поверхности `S = 6*a^2`
1) `S_(мал) = 6*a^2`
2) `S_(бол) = 6*(a+1)^2`
3) `6*(a+1)^2=6*a^2+54`
`6*(a^2+2a+1)=6a^2+54`
`6a^2+12a+6=6a^2+54`
`12a=48`
`a=4`
Ответ: 4
mathege
Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
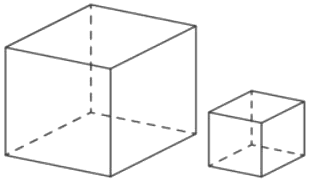
Решение:
Объем куба `V=a^3`
Площадь поверхности `S = 6*a^2`
1) `V_(бол)/V_(мал) = 8 ⇒ (AB^3)/a^3=8 ⇒ AB^3=8*a^3`
`AB=2a`
2) `S_(мал) = 6a^2`
`S_(бол) = 6*(2a)^2=6*4a^2=24a^2`
`24/6=4` раза
Ответ: 4
mathege
Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

Решение:
Объем куба `V=a^3`
1) `V_(мал) = a^3`
2) `V_(бол) = (a+1)^3`
3) `(a+1)^3=a^3+19`
`(a+1)^2*(a+1)`
`(a^2+2a+1)(a+1) = a^3+19`
`a^3+a^2+2a^2+2a+a+1=a^3+19`
`3a^3+3a-18=0`
`a^2+a-6=0`
`a_1=-3`
`a_2=2`
Ответ: 2
mathege
В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 точка 𝐾 — середина ребра 𝐵𝐶, точка 𝐿 — середина ребра 𝐶𝐷, точка 𝑀 — середина ребра 𝐶𝐶1. Найдите угол 𝑀𝐿𝐾. Ответ дайте в градусах.
Решение:
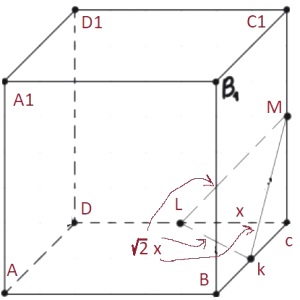
ΔMLK равносторонний, тогда ∠MLK =60°
Ответ: 60
mathege
Параллелепипед
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известно, что BB1=16, A1B1=2, A1D1=8. Найдите длину диагонали AC1.
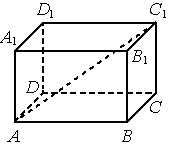
Решение:
1) ΔABC `AC=sqrt(2^2+8^2) =sqrt68`
2) ΔACC1 `AC_1=sqrt(16^2+sqrt68^2) =sqrt324=18`
Ответ: 18
Номер: D6AA89
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известны длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C.

Решение:
∠BB1C - искомый
1) ΔBB1C `B_1C=sqrt(12^2+16^2)=sqrt400=20`
2) `sin∠BB_1C = 16/20=0,8`
Ответ: 0,8
Номер: 0628B5
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известны длины рёбер: 𝐴𝐵=7, 𝐴𝐷=3, 𝐴𝐴1=4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки 𝐴, 𝐵 и 𝐶1.
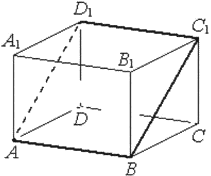
Решение:
1) ΔBCC1: `BC_1=sqrt(3^2+4^2)=5`
2) `S_(ABC_1D_1) =7*5=35`
Ответ: 35
Номер: 4335
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известны длины рёбер: AB=15, AD=8, AA1=21. Найдите площадь сечения, проходящего через вершины B, B1 и D.

Решение:
1) BDD1B1 - сечение
2) ΔABD: `BD=sqrt(15^2+8^2) = sqrt(255+64)=sqrt289=17`
3) `S_(BDD_1B_1) = 21*17=357`
Ответ: 357
Номер: 22DA45
Найдите объём многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1, у которого AB=3, AD=4, AA1=5.
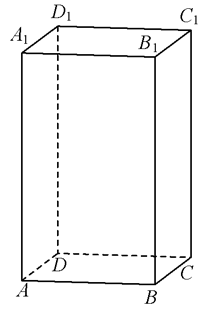
Решение:
Объем параллелепипеда V = abh
`V =1/2*V_(пар.)=1/2*3*4*5=30`
Ответ: 30
Номер: C352F6
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известно, что AB=5, BC=4, AA1=3. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A1, B1.

Решение:
Объем параллелепипеда
V = abh
`V =1/2*V_(пар)=1/2*3*4*5=30`
Ответ: 30
Номер: 32AF22
Найдите угол 𝐴𝐵𝐷1 прямоугольного параллелепипеда, для которого 𝐴𝐵=5, 𝐴𝐷=4, 𝐴𝐴1=3. Ответ дайте в градусах.
Решение:

1) ΔABD1 - прямоугольный.
2) ΔAA1D1 `AD_1=sqrt(4^2+3^2) =5`
3) ΔABD1 - прямоугольный и равнобедренный.
∠ABD1=45°
Ответ: 45
ЕГЭ 2014
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объём параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Решение:
Объем параллелепипеда
V = abh
48 = 6*2*h
h = 48/12=4
Ответ: 4
mathege
Рёбра прямоугольного параллелепипеда равны 1, 2, 3. Найдите площадь его поверхности.

Решение:
Площадь поверхности параллелепипеда
`S = 2ab+2ah+2bh`
`S_(пов) = 2+2+3+3+6+6=22`
Ответ: 22
mathege
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Решение:
Объем параллелепипеда V=abh
Пусть AC - диагональ параллелепипеда, BC - диагональ нижней стороны, D - нижний угол, ближайший к нам.
1) ΔBCD: `BC=sqrt(4^2+2^2) = sqrt20`
2) ΔABC: `AB=sqrt(6^2+sqrt20^2) = 4`
3) `V_(пар.) = 4*2*4=32`
Ответ: 32
mathege
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.

Решение:
Площадь поверхности параллелепипеда.
`S = 2ab+2ah+2bh`
Пусть DC - диагональ параллелепипеда, AC - диагональ нижней стороны, B - нижний угол, ближайший к нам.
1) ΔABC: `AC = sqrt(2^2+4^2)=sqrt20`
2) ΔACD: `AD = sqrt(6^2+sqrt20^2)=sqrt16=4`
3)`S = 8+8+16+16+8+8=64`
Ответ: 64
mathege
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известно, что 𝐴𝐵=24, 𝐴𝐷=7, 𝐴𝐴1=25. Найдите угол 𝐷𝐵𝐷1. Ответ дайте в градусах.
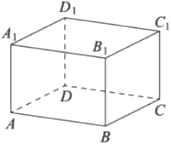
Решение:
1) ΔABD: `BD =sqrt(24^2+7^2)=sqrt625=25`
2) ΔBDD1 - прямоугольный равнобедренный ⇒ ∠DBD1 = 45º
Ответ: 45
mathege
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 ребро 𝐴𝐵=2, ребро 𝐴𝐷=√5, ребро 𝐴𝐴1=2. Точка 𝐾− середина ребра 𝐵𝐵1. Найдите площадь сечения, проходящего через точки 𝐴1, 𝐷1 и 𝐾.
Решение:
1) ΔA1B1K: `A_1K=sqrt(2^2+1^2)=sqrt5`
2) `S_(A1D1EK) = sqrt5^2=5`
Ответ: 5
mathege
Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна √8 и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.
Решение:
Объем параллелепипеда V = abh
1) `∠AC C_1=180-90-45=45` ⇒ ΔACC1 прямоугольный и равнобедренный.
2) ΔACC1:
`sqrt8^2=x^2+x^2`
`8=2*x^2`
`x^2=4`
`x=2`
3) ΔACD:
`2^2=AD^2+AD^2`
`4=2AD^2`
`AD=sqrt2`
4) `V = sqrt2*sqrt2*2=sqrt4*2=2*2=4`
Ответ: 4
mathege
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 60° и равно 2. Найдите объем параллелепипеда.
Решение:
Площадь параллелограмма через угол.
S = ac*sin∝ (∝ угол между сторонами a и c)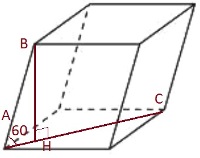
1) ΔABH:
`sin60=(BH)/2`
`sqrt3/2=(BH)/2`
`BH=sqrt3`
2) `S_(ромб)=1*1*sin60=sqrt3/2`
3) `V_(паралл.) = S*h = sqrt3/2*sqrt3=sqrt9/2=3/2=1,5`
Ответ: 1,5
mathege
Призма
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 2 и 7, боковое ребро призмы равно 6. Найдите объём призмы.
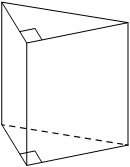
Решение:
Площадь прямоугольного треугольника
`S=(ab)/2`
Объем призмы
`V = S_(осн)*h`
1)`S=(2*7)/2=7`
2)`V = 7*6=42`
Ответ: 42
Номер: C2CADE
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 7, объём призмы равен 56. Найдите боковое ребро призмы.

Решение:
Площадь прямоугольного треугольника
`S=(ab)/2`
Объем призмы
`V = S_(осн)*h`
1) `S=(4*7)/2=14`
2)`56 = 14*h`
`h = 4`
Ответ: 4
Номер: 872654
В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1, все рёбра которой равны 1, найдите угол между прямыми AA1 и BC1.
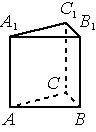
Решение:
1) Искомый угол ∠B1BC1
2) Рассмотрим ΔB1BC1, он прямоугольный и равнобедренный. Тогда углы у основания `(180-90)/2 =45` º
Ответ: 45
Номер: C0F645
Впишите правильный ответ.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсечённой треугольной призмы равен 15.
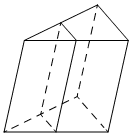
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
Объем призмы V=Sосн*h
Отношение площадей подобных треугольников равно квадрату коэффициента подобия
Соотношение объемов между треугольными призмами будет равно соотношению площади треугольников (низ рисунка), так как они являются площадью основания, а высота у них одинаковая.
Причем, так как это средняя линия, то она меньше основания треугольника в 2 раза, и высота треугольника тоже меньше в 2 раза, то есть площадь треугольников соотносится как 1:4
15*4=60
Ответ: 60
Номер: 817F71
Через среднюю линию основания треугольной призмы, объём которой равен 48, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.
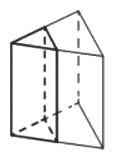
Решение:
Объем призмы
`V = S_(осн)*h`
Отношение площадей подобных треугольников равно квадрату подобия.
1) `V_(больш.приз) = 48 =S_(больш.Δ)*h`
2) `(S_(больш.Δ))/(S_(мал.Δ))=2^2 ⇒ S_(мал.Δ)=1/4*S_(больш.Δ)`
3) `V_(мал.приз) = S_(мал.Δ)*h = 1/4*S_(больш.Δ)*h =1/4*48=12`
Ответ: 12
Номер: 4374
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
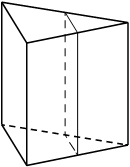
Решение:
Обозначим стороны маленького треугольника за a b c
1) `S_(бок.пов.мал.) = ah+bh+ch=37`
2) `S_(бок.пов.бол.) = 2ah+2bh+2ch=2(ah+bh+ch)=2*37=74`
Ответ: 74
Номер: AB1F5D
Площадь боковой поверхности треугольной призмы равна 75. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Решение:
Обозначим стороны маленького треугольника за a b c
1) `S_(бок.пов.бол.) = 2ah+2bh+2ch=2(ah+bh+ch)=75`
2) `S_(бок.пов.мал.) = ah+bh+ch=37,5`
Ответ: 37,5
Номер: 5DADB7
В правильной четырёхугольной призме 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известно, что BD1=2AD. Найдите угол между диагоналями DB1 и CA1. Ответ дайте в градусах.
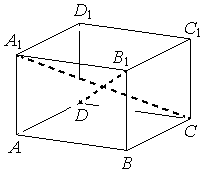
Решение:
Обозначим пересечение диагоналей точкой О
`ΔA_1OB_1` равносторонний, значит
`ΔA_1OB_1=60`º
Ответ: 60
Номер: A629B5
В правильной четырёхугольной призме 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 ребро 𝐴𝐴1 равно 15, а диагональ 𝐵𝐷1 равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки 𝐴, 𝐴1 и 𝐶.
Решение:
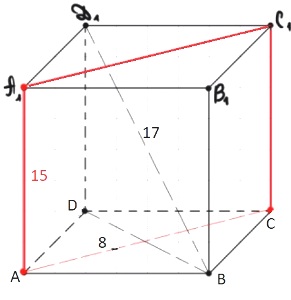
1) ΔBDD1: `BD=sqrt(17^2-15^2)=sqrt64=8`
AC=8
2) `S_(AC C_1A_1) =15*8=120`
Ответ: 120
ЕГЭ 2015
В правильной шестиугольной призме 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1, все рёбра которой равны 3, найдите угол между прямыми 𝐶𝐷 и 𝐸1𝐹1. Ответ дайте в градусах.
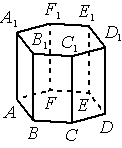
Решение:
Продолжим прямые F1E1 и C1D1 до пересечения в точке K.
1) ∠E1KD - искомый
2)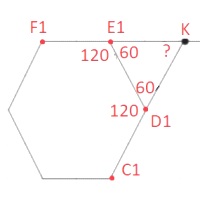
∠KE1D1=180°-120°=60°
∠KD1E1=180°-120°=60° ⇒ ∠E1KD1=180°-2*60°=60°
Ответ: 60
Номер: 257041
Найдите объём многогранника, вершинами которого являются точки 𝐷, 𝐸, 𝐹, 𝐷1, 𝐸1, 𝐹1 правильной шестиугольной призмы 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1, площадь основания которой равна 8, а боковое ребро равно 9.

Решение:
Площадь части основания правильного шестиугольника, равная треугольнику, - между любой вершиной и двумя углами через эту вершину, равна 1/6 части от всего основания: `S_(ABC) = 1/6*S`
Объем призмы `V = S_(осн)*h`
1) `S_(FED)=1/6*8=4/3`
2)`V=4/3*9=12`
Ответ: 12
Номер: 02836B
Найдите объём многогранника, вершинами которого являются вершины 𝐴, 𝐶, 𝐷, 𝐹, 𝐴1, 𝐶1, 𝐷1, 𝐹1 правильной шестиугольной призмы 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1, площадь основания которой равна 9, а боковое ребро равно 11.
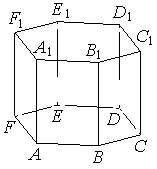
Решение:
Площадь части основания правильного шестиугольника, равная прямоугольнику, - между четырьмя вершинами напротив друг друга, равна 2/3 части от всего основания: `S_(ABDE) = 2/3*S`
Объем призмы `V = S_(осн)*h`
1) `S_(ACDF) = 2/3*9=6`
2) `V_(иск) = 6*11=66`
Ответ: 66
Номер: BCD10D
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

Решение:
Площадь прямоугольного треугольника
`S=(ab)/2`
1) `a^2=6^2+8^2=100`
`a=10`
2)`S_(пов)=(6*8)/2+(6*8)/2+80+60+100=288`
Ответ: 288
mathege
В правильной треугольной призме 𝐴𝐵𝐶𝐴1𝐵1𝐶1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер 𝐴𝐵, 𝐴𝐶, 𝐴1𝐵1 и 𝐴1𝐶1.
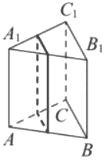
Решение:
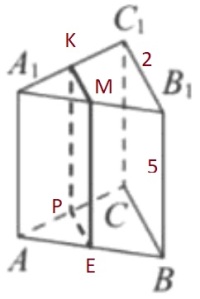
1) `ME=5`
`KM=1/2*2=1`
2) `S_(KMEP)=5*1=5`
Ответ: 5
mathege
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

Решение:
Sпов = 1760=400+400+20h+20h+20h+20h
1760 = 800+80h
960=80h
h=12
Ответ: 12
mathege
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
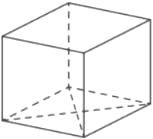
Решение:
Площадь ромба
`S = (d_1*d_2)/2`
1) `a^2=3^2+4^2`
`a=5`
2) `S_(пов) = (6*8)/2+(6*8)/2+50+50+50+50=248`
Ответ: 248
mathege
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.

Решение:
Площадь ромба = произведение диагоналей пополам
`S = (d_1*d_2)/2`
1) `a^2=3^2+4^2`
`a=5`
2) `S_(пов)=248=(6*8)/2+(6*8)/2 +5h+5h+5h+5h`
`248=48+20h`
`200=20h`
`h=10`
Ответ: 10
mathege
Площадь поверхности правильной треугольной призмы равна 10. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в два раза, а форма останется прежней?
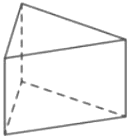
Решение:
Площадь равностороннего треугольника
`S = (sqrt3*a^2)/4`
1) `S_1 = (sqrt3*a^2)/4+(sqrt3*a^2)/4+3ah=10`
2) `S_2= (sqrt3*(2a)^2)/4+(sqrt3*(2a)^2)/4+3*2a*2h=4((sqrt3*a^2)/4+(sqrt3*a^2)/4+3ah)=4*10=40`
Ответ: 40
mathege
Сторона основания правильной шестиугольной призмы равна 5, высота равна 10. Найдите площадь боковой поверхности призмы.
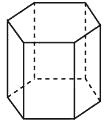
Решение:
`S_(бок.пов) =5*10*6=300`
Ответ: 300
mathege
В правильной шестиугольной призме 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1 все ребра равны 1. Найдите тангенс угла 𝐴𝐷1𝐷.
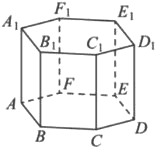
Решение:
Диагонали равностороннего шестиугольника срединная и следующая соотносятся как `sqrt3*a` и 2a.
1) AD=2*1=2
2) `tg_(AD_1D)=2/1=2`
Ответ: 2
mathege
В правильной шестиугольной призме 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1 все ребра равны 1. Найдите угол 𝐴𝐶1𝐶. Ответ дайте в градусах.

Решение:
Диагонали равностороннего шестиугольника срединная и следующая соотносятся как `sqrt3*a` и 2a.
1) `AC=sqrt3*1=sqrt3`
2) `tg_(AC_1C)=sqrt3/1=sqrt3` ⇒ ∠AC1C=60º
Ответ: 60
mathege
В правильной шестиугольной призме 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1 все ребра равны √5. Найдите расстояние между точками 𝐵 и 𝐸1.

Решение:
Диагонали равностороннего шестиугольника срединная и следующая соотносятся как `sqrt3*a` и 2a.
1) `BE=2sqrt5`
2) ΔBEE1:
`BE_1=sqrt(sqrt5^2+(2sqrt5)^2)=sqrt25=5`
Ответ: 5
mathege
В правильной шестиугольной призме 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1 все ребра равны 1. Найдите расстояние между точками 𝐴 и 𝐸1.

Решение:
Диагонали равностороннего шестиугольника срединная и следующая соотносятся как `sqrt3*a` и 2a.
1) `AE=sqrt3*1`
2) ΔAEE1: `AE_1=sqrt(sqrt3^2+1^2)=sqrt4=2`
Ответ: 2
mathege
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны √3.
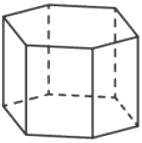
Решение:
Объем призмы
`V = S_(осн)*h`
Площадь равностороннего шестиугольника
`S = (3sqrt3a^2)/2`
1) `S_(осн) = (3sqrt3*1^2)/2=(3sqrt3)/2`
2) `V_(призм) = (3sqrt3)/2 * sqrt3 = (3*sqrt9)/2=9/2=4,5`
Ответ: 4,5
mathege
Найдите объём призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые рёбра равны 2√3 и наклонены к плоскости основания под углом 30°.
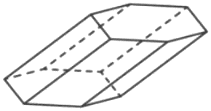
Решение:
Объем призмы
`V = S_(осн)*h`
Площадь равностороннего шестиугольника
`S = (3sqrt3a^2)/2`
1) `BC = 1/2*2sqrt3=sqrt3`
2) `S_(осн) = (3sqrt3*2^2)/2=6sqrt3`
3) `V_(пр) = 6sqrt3*sqrt3=6sqrt9=6*3=18`
Ответ: 18
mathege
В сосуде, имеющем форму правильной треугольной призмы, уровень жидкости достигает 80 см. На какой высоте будет находиться уровень жидкости, если её перелить в другой сосуд такой же формы, сторона основания которого в 4 раза больше, чем у первого? Ответ дайте в сантиметрах.
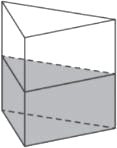
Решение:
Объем призмы
`V = S_(осн)*h`
Площадь равностороннего треугольника
`S = (sqrt3*a^2)/4`
1) `V_(вод) = S_(осн)*80=(sqrt3*a^2)/4*80 = 20sqrt3*a^2`
2) `20sqrt3*a^2=(sqrt3*(4a)^2)/4*h`
`h =5`
Ответ: 5
mathege
В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см3.

Решение:
Объем призмы
`V = S_(осн)*h`
1) `V_(вод) = S_(осн)*25`
`2300=S_(осн)*25`
`S_(осн)*25 = 92`
2) `V_(вод) + V_(дет) = S_(осн) *27`
`2300+V_(дет)=92*27`
`2300+V_(дет)=2484`
`V_(дет)=2484-2300=184`
Ответ: 184
mathege
Цилиндр
Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра.
Решение:
Площадь боковой поверхности
S = 2πRh
1) `S_(бок) = 12π=2πRh`
6=Rh
6=3h
h=2
Ответ: 2
Номер: B29C5A
Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
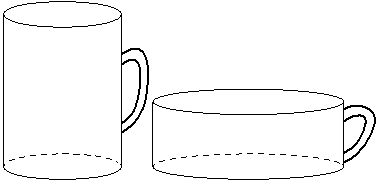
Решение:
Объем цилиндра
`V = πR^2h`
1) `V_1 = πR^2h`
2) `V_2 = π(3R)^2*h/2 = 9/2*πR^2*h`
3) `V_2/V_1=(4,5πR^2*h)/(πR^2*h)=4,5`
Ответ: 4,5
Номер: 4BD794
В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в см.
Решение:
Объем цилиндра
`V = πR^2h`
Диаметр в 2 раза больше, значит радиус также в 2 раза больше.
1) `V_(вод)=πR^2*48`
2) `V_(вод)=π(2R)^2*h`
3) `πR^2*48=4πR^2*h`
`48=4*h`
`h=12`
Ответ: 12
Номер: 0BE824
В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 5 раз меньше диаметра первого? Ответ выразите в сантиметрах.
Решение:
Объем цилиндра
`V = πR^2h`
1) `V_(вод)=πR^2*2`
2) `V_(вод)=π(R/5)^2*h`
3) `πR^2*2=(πR)/25*h`
`2=h/25`
`h=50`
Ответ: 50
Номер: BDAC50
В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см.
Решение:
Объем цилиндра
`V = πR^2h`
1)`V_(вод) = 500=πR^2*h`
2)`V_(вод)+V_(дет) = 1,2*500`
`V_(дет) =100`
Ответ: 100
Номер: EBB312
В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. Ответ выразите в куб. см.
Решение:
Объем цилиндра
`V = πR^2h`
1)`V_(вод) = 2800=πR^2*16`
2)`V_(вод)+V_(дет) = πR^2*29`
`2800+V_(дет) = 175*29`
`V_(дет) = 5075-2800=2275`
Ответ: 2275
Номер: 791637
В цилиндрический сосуд, в котором находится 6 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
Решение:
Пусть плоскость основания цилиндра равна Sосн дм2, а высота жидкости в сосуде равна h см.
Тогда объем жидкости в сосуде будет равен:
V1 = Sосн * h см3 = 6 дм3.
После погружения в сосуд детали, уровень жидкости стал равен 1,5 * h дм.
Так как уровень жидкости поднялся в 1,5 раза, то и объем увеличится в 1,5 раза.
V2 = Sосн * 1,5 * h = 6 *1,5 = 9дм3.
Тогда разность объемов есть объем погруженной детали.
V = V2 – V1 = 9 – 6 = 3 дм3.
Ответ: 3
Номер: 590166
Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
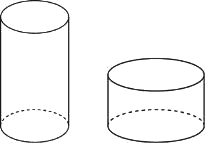
Решение:
Объем цилиндра
`V = πR^2h`
1) `V_1 = πR^2h=12`
2 `V_2 = π(R/2)^2*3h=3/4*πR^2h=9`
Ответ: 9
ЕГЭ 2017, 2019
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Решение:
Длина окружности
С = 2πR
Площадь боковой поверхности
S = 2πRh
1) C = 2πR =3
2) S = 2πR*h = 3*2=6
Ответ: 6
mathege
Конус
Диаметр основания конуса равен 40, а длина образующей – 25. Найдите высоту конуса.
Решение:
`25^2=20^2+h^2`
`h^2=225`
`h=15`
Ответ: 15
Номер: 50FCF3
Высота конуса равна 21, а длина образующей равна 29.

Найдите диаметр основания конуса.
Решение:
`29^2=21^2+r^2`
`r^2=400`
`r=20`
`d=20*2=40`
Ответ: 40
Номер: 0ABBF1
Высота конуса равна 24, а диаметр основания равен 90. Найдите образующую конуса.
Решение:
`l^2=24^2+45^2`
`l^2=2601`
`l=51`
Ответ: 51
Номер: E29891
Площадь основания конуса равна 36𝜋, высота – 10. Найдите площадь осевого сечения этого конуса.
Решение:
Площадь круга:
`S = πR^2`
1) `S_(осн) = 36π=πR^2`
`R=6`
2) `S_(иск) = 1/2*12*10=60`
Ответ: 60
Номер: 4377
Высота конуса равна 40, а длина образующей – 58. Найдите площадь осевого сечения этого конуса.

Решение:
Площадь треугольника
`S = 1/2*a*h`
1) `58^2=40^2+R^2`
`R^2=58^2-40^2=(58-40)(58+40)=18*98=9*196`
`R=3*14=42`
2) `S_(тр)=1/2*84*40=1680`
Ответ: 1680
Номер: 4440
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
Решение:
Объем конуса
`V = 1/3πR^2h`
1) `V_1=1/3*πR^2h`
2) `V_2=1/3*πR^2h/3=1/3*1/3*πR^2h`
в 3 раза
Ответ: 3
ЕГЭ 2019
Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 8 раз, а высоту оставить прежней?
Решение:
Объем конуса
`V = 1/3πR^2h`
1)`V_1 = (1/3πR^2h)`
2)`V_2 = 1/3π(8R)^2h=64*(1/3πR^2h)`
в 64 раза
Ответ: 64
Номер: F9E66F
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
Решение:
Площадь боковой поверхности конуса
`S = πRl`
1) `S_1 = πRl`
2) `S_2 = πR*3l=3*πRl`
в 3 раза
Ответ: 3
ЕГЭ 2018
Площадь основания конуса равна 48. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 4 и 12, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Решение:
Площадь круга:
`S = πR^2`
1) K подобия конусов = `16/4=4`
2) K подобия конусов = `R_б/R_м =4` => пусть R - радиус маленького круга, 4R - радиус большого круга.
3) `S_(б.круга) = 48 = π(4R)^2`
`48=16πR^2`
`πR^2 =3`
4) `S_(м.круга) = πR^2 =3`
Ответ: 3
Номер: 4419
Площадь полной поверхности конуса равна 32,5. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 4:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
Решение:
Площадь боковой поверхности конуса
`S = πRl`
1) `K_(подобия конусов) = (5x)/(4x)=5/4=R_(бол)/R_(мал)=l_(бол)/l_(мал)`
2) `S_(пов. бол.) = 32,5=π(5/4R)^2+π*5/4*R*5/4*l`
`32,5=25/16*πR^2+25/16*πRl`
`32,5=25/16(πR^2+πRl)`
`πR^2+πRl = (32,5*16)/25=104/5`
3) `S_(пов. мал.) = πR^2+πRl=104/5=20,8`
Ответ: 20,8
Номер: 4F5B93
Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
Решение:
Площадь поверхности конуса
`S = πR^2+πRl`
1) `K_(подобия конусов) = (5x)/(3x)=5/3=R_(бол)/R_(мал)=l_(бол)/l_(мал)`
2) `S_(пов. бол.) = 35=π(5/3R)^2+π*5/3*R*5/3*l`
`35=25/9*πR^2+25/9*πRl`
`35=25/9(πR^2+πRl)`
`πR^2+πRl = (35*9)/25=63/5=12,6`
3) `S_(пов. мал.) = πR^2+πRl=12,6`
Ответ: 12,6
Номер: 0C55B6
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение:
Отношение объемов подобных конусов
`V_1/V_2 = k^3`
`k=2`
1) `V_б/V_м = k^3`
`V_б/25 = 2^3`
`V_б=200`
2) `V_(иск) =200-25=175`
Ответ: 175
Номер: 60E82D
В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение:
Отношение объемов подобных конусов
`V_1/V_2 = k^3`
1) `k=h/(2/3h)=3/2`
2) `V_б/144 = (3/2)^3`
`V_б =(27*144)/8=486`
3) `V_(иск) =486-144=342`
Ответ: 342
Номер: 06254C
Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Решение:
Площадь боковой поверхности конуса
`S = πRl`
Длина окружности
`С=2πR`
1) `С = 2πR = 3`
`πR=1,5`
2) `S = πR*l=1,5*l=1,5*2=3`
Ответ: 3
mathege
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Решение:
Площадь боковой поверхности конуса
`S = πRl`
Площадь круга:
`S = πR^2`
1) `S_(бок)=2S_(осн)`
`πRl=2πR*R`
`l=2R`
2) `cos∝=(1R)/(2R) = 1/2`
`∝=60°`
Ответ: 60
mathege
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение:
Отношение объемов подобных конусов
`V_1/V_2 = k^3`
`k = 2`
1) `16/V_(мал)= 2^3`
2) `V_(мал)= 2`
Ответ: 2
mathege
Пирамида
Найдите объём многогранника, вершинами которого являются точки 𝐶, 𝐴1, 𝐵1, 𝐶1 правильной треугольной призмы 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 4, а боковое ребро равно 9.

Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
`V_(A_1B_1C_1C) = 1/3*4*9=12`
Ответ: 12
Номер: C6FDB6
Найдите объем многогранника, вершинами которого являются вершины 𝐴, 𝐵, 𝐶, 𝐷, 𝐵1 прямоугольного параллелепипеда 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1, у которого 𝐴𝐵=9, 𝐵𝐶=3, 𝐵𝐵1=8.
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
`V = 1/3*3*9*8=72`
Ответ: 72
Номер: 5188 (аналог 29FE0E)
Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐴1, 𝐵1, 𝐶1.
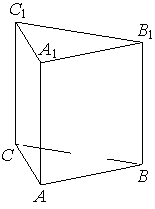
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
`V_(пир A_1B_1C_1A)=1/3*9*4=3*4=12`
Ответ: 12
Номер: FBF62F
В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 известно, что 𝐴𝐵=6, 𝐵𝐶=5, 𝐴𝐴1=4. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐵, 𝐶, 𝐵1.

КЭС: 5.3 Многогранники 5.5 Измерение геометрических величин
Решение:
Объем ABCB1 составляет 1/6 от ABCDA1B1C1D1, так как это пирамида
`V=1/3 * S_(осн.) * h`
В то время как параллелепипед V= Sосн. * h, то есть здесь при том же основании пирамида меньше параллелепипеда в три раза.
Да к тому же еще и площадь основания меньше в 2 раза, так как делится по диагонали. В итоге 2*3=6 - во столько раз соотносятся объемы фигур.
Тогда
`(6*5*4)/6`=20
Ответ: 20
Номер: B28DB5
Объём правильной четырёхугольной пирамиды 𝑆𝐴𝐵𝐶𝐷 равен 116. Точка 𝐸− середина ребра 𝑆𝐵. Найдите объём треугольной пирамиды 𝐸𝐴𝐵𝐶.
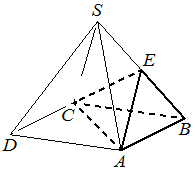
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) `V_(SABCD) = 116=1/3*S_(ABCD)*h`
`S_(ABCD)*h=116*3=348`
2) `V_(EABC) = 1/3 * S_(ABC)*h/2=1/3*1/2*S_(ABCD)*1/2*h=1/12*S_(ABCD)*h=1/12*348=29`
Ответ: 29
Номер: 943A2F
В правильной четырёхугольной пирамиде 𝑆𝐴𝐵𝐶𝐷 с вершиной 𝑆 точка 𝑂− центр основания, 𝑆𝑂=35, 𝑆𝐷=37. Найдите длину отрезка 𝐵𝐷.
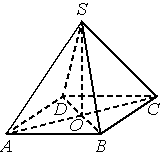
Решение:
ΔSAO
`AO=sqrt(37^2-35^2) = sqrt((37-35)(37+35))=sqrt144=12`
`AC=2*12=24=BD`
Ответ: 24
Номер: C026C8
В правильной четырёхугольной пирамиде 𝑆𝐴𝐵𝐶𝐷 с основанием 𝐴𝐵𝐶𝐷 боковое ребро 𝑆𝐶 равно 37, сторона основания равна 35√2. Найдите объём пирамиды.
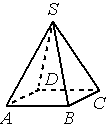
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) ΔABC:
`AC=sqrt((35sqrt2)^2+(35sqrt2)^2)=sqrt(35^2*2+35^2*2)=sqrt(4*35^2)=2*35=70`
2) ΔSOC:
`SO=sqrt(37^2-35^2)=sqrt((37-35)(37+35))=sqrt144=12`
3) `V=1/3(35sqrt2)^2*12=1225*8=9800`
Ответ: 9800
Номер: 0940E2
В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.
Решение:
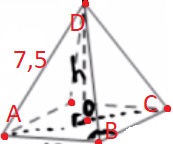
1) ΔABC:
`AC=sqrt(10^2+10^2)=sqrt200=sqrt(100*2)=10sqrt2`
2) ΔAОD:
`OD=sqrt((15/2)^2-(5sqrt2)^2) =sqrt(225/4-50/1)=sqrt(25/4)=2,5`
Ответ: 2,5
Номер: 59DC27
В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.
Решение:
Радиус окружности описанной около равностороннего треугольника.
`R = (sqrt3*a)/3`
`R = 2/3*h`
1) `R=sqrt3*(10,5)/3=3,5sqrt3=(7sqrt3)/2`
2) `h=sqrt(7^2-(7sqrt3/2)^2) = sqrt(49/1-(49*3)/4)=sqrt(49/4)=3,5`
Ответ: 3,5
Номер: 9726B0
В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 4. Найдите её объём.

Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) ΔCOD
`OC=sqrt(4^2-2^2)=sqrt12=2sqrt3`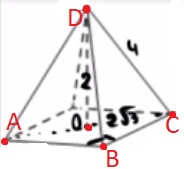
2) ΔABC:
`(4sqrt3)^2=x^2+x^2`
`48=2x^2`
`x^2=24`
3) `V=1/3*24*2=16`
Ответ: 16
Номер: F26E93
Объём треугольной пирамиды равен 78. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рисунок). Найдите объём отсечённой треугольной пирамиды.
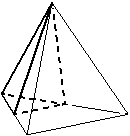
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Отношение площадей подобных треугольников
`S_1/S_2=k^2`
1) `V_(бол)=1/3*S_(осн. бол.)*h=78` ⇒ `S_(осн. бол.)*h=234`
2) `V_(мал)=1/3*S_(осн. мал.)*h=1/3*1/4*S_(осн. бол.)*h=1/12*234=19,5`
Ответ: 19,5
Номер: 06A191
В правильной четырёхугольной пирамиде все рёбра равны 2. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
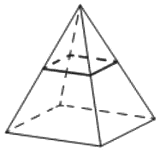
Решение:
S=1*1=1
Ответ: 1
Номер: 4482
Дана правильная четырёхугольная призма 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1, площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐵, 𝐶, 𝐴1, 𝐵1.
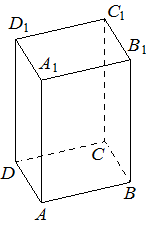
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
1) AB*CB=6
2) `V_(AB B_1A_1C)=1/3*7*AB*CB=1/3*7*6=14`
Ответ: 14
Номер: EFF329
Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 8, а боковое ребро равно 6. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐶, 𝐴1, 𝐵1, 𝐶1.
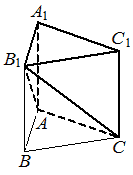
КЭС: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность; прямая призма; правильная призма 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида 5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Решение:
BACB1 - это пирамида, объем которой равен `1/3*S_(основания) *h`
Объем призмы равен `S_(основания)*h`.
`V_(приз.)=8*6=48`
`V_(ABCB_1)=1/3*8*6=16`
Объем ACA1B1C1 находится как разность объемов призмы и пирамиды
`V=48-16=32`
Ответ: 32
Номер: F277BE
Найдите объём многогранника, вершинами которого являются вершины 𝐴, 𝐶, 𝐴1, 𝐵1, 𝐶1 правильной треугольной призмы 𝐴𝐵𝐶𝐴1𝐵1𝐶1. Площадь основания призмы равна 7, а боковое ребро равно 9.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Объем призмы
`V = S_(осн)*h`
1) `V_(призм) = 7*9=63`
2) `V_(ABCB_1) = 1/3*7*9=21`
3) `V_(иск) = 63-21=42`
Ответ: 42
Номер: 805979
Найдите объём многогранника, вершинами которого являются вершины 𝐴, 𝐶, 𝐴1, 𝐵1 правильной треугольной призмы 𝐴𝐵𝐶𝐴1𝐵1𝐶1. Площадь основания призмы равна 9, а боковое ребро равно 4.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
1) `V_(призм)=9*4=36`
2) `V_(ABCB_1)=1/3*9*4=12`
3) `V_(A_1B_1C_1C)=1/3*9*4=12`
4) `V_(иск)=36-12-12=12`
Ответ: 12
Номер: D4DB81
Найдите объём многогранника, вершинами которого являются точки 𝐷, 𝐴1, 𝐵1, 𝐶1, 𝐷1, 𝐸1, 𝐹1 правильной шестиугольной призмы 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1, площадь основания которой равна 12, а боковое ребро равно 2.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
`V=1/3*12*2=8`
Ответ: 8
Номер: 362938
Найдите объём многогранника, вершинами которого являются вершины 𝐴1, 𝐵1, 𝐹1, 𝐴 правильной шестиугольной призмы 𝐴𝐵𝐶𝐷𝐸𝐹𝐴1𝐵1𝐶1𝐷1𝐸1𝐹1, площадь основания которой равна 12, а боковое ребро равно 15.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Площадь части основания правильного шестиугольника, равная отсеченному треугольнику (между любой вершиной и двумя соседними углами), равна 1/6 части от всего основания.
1) `S_(A_1B_1F_1)=1/6*12=2`
2) `V_(иск)=1/3*2*15=10`
Ответ: 10
Номер: 285ADD
В правильной шестиугольной пирамиде боковое ребро равно 6,5, а сторона основания равна 2,5. Найдите высоту пирамиды.
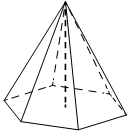
Решение:
Радиус окружности, описанной около равностороннего шестиугольника, равен стороне этого шестиугольника.
1) `R=2,5`
2) `h=sqrt(6,5^2-2,5^2)=sqrt(42,25-6,25)=6`
Ответ: 6
Номер: 5912F6
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
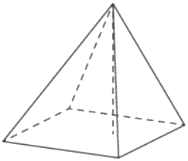
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
`16=1/3*4*3*h`
`16=4h`
`h=4`
Ответ: 4
mathege
Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной – центр куба.
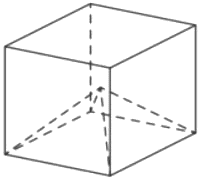
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
Объем куба
`V = a^3`
1) `V = a^3=12`
2) `V_(пир.) = 1/3*a^2*1/2*a=1/6*a^3=1/6*12=2`
Ответ: 2
mathege
Объём параллелепипеда 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 равен 12. Найдите объём треугольной пирамиды 𝐵1𝐴𝐵𝐶.
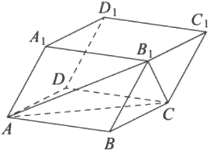
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) `V_(пар)=S_(ABCD)*h=12`
2) `V_(B_1ABC)=1/3*1/2*S_(ABCD)*h=1/3*1/2*12=2`
Ответ: 2
mathege
Найдите объем параллелепипеда 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1, если объем треугольной пирамиды 𝐴𝐵𝐷𝐴1 равен 3.
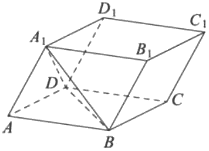
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
1) `V_(ABDA_1) = 1/3*S_(ABD)*h=3`
`S_(ABD)*h=9`
2) `V_(пар) = 2*S_(ABD)*h=2*9=18`
Ответ: 18
mathege
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна √3.
Решение:
Объем пирамиды
`V = 1/3*S_(осн.)*h`
Площадь равностороннего треугольника
`S =(sqrt3*a^2)/4`
1) `S_(осн)=(sqrt3*1^2)/4=sqrt3/4`
2) `V_(пир)=1/3*sqrt3/4*sqrt3=sqrt9/(3*4)=1/4=0,25`
Ответ: 0,25
mathege
Стороны основания правильной четырёхугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Решение:
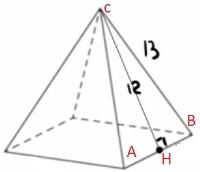
1) `CH=sqrt(13^2-5^2)=12`
2) `S_(пов)=10*10+4S_(ABC)=100+4*1/2*10*12=340`
Ответ: 340
mathege
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 24 и высота равна 16.
Решение:
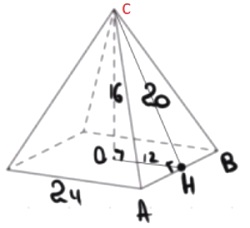
1) `OH=1/2*24=12`
2) ΔOCH:
`CH=sqrt(16^2+12^2)=sqrt400=20`
3) `S_(ABC)=1/2*24*10=240`
4) `S_(бок)=4*240=960`
Ответ: 960
mathege
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Решение:
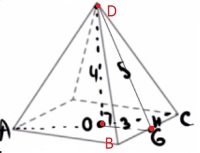
1) `OH=1/2*6=3`
2) ΔDOH: `DH=sqrt(4^2+3^2)=5`
3) `S_(BCD)=1/2*6*5=15`
4) `S_(осн)=6*6=36`
5) `S_(пов)=36+4*15=96`
Ответ: 96
mathege
Во сколько раз увеличится объём пирамиды, если её высоту увеличить в четыре раза?
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
`V_1/V_2=(1/3*S*h)/(1/3*S*4h)=1/4`
в 4 раза
Ответ: 4
mathege
Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Решение:
1) `S_(пов.м)=a^2+4*1/2*a*h=a^2+2ah`
2) `S_(пов.б)=(2a)^2+4*1/2*2a*2h=4(a^2+2ah)`
в 4 раза
Ответ: 4
mathege
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
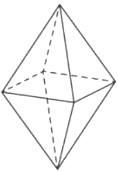
Решение:
1) `S_(пов.исх)=8*1/2*a*h`
2) `S_(пов.нов)=8*1/2*3a*3h=9*(8*1/2*a*h)`
в 9 раз
Ответ: 9
mathege
Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
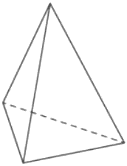
Решение:
Площадь равностороннего треугольника
`S =(sqrt3*a^2)/4`
1) `S_(пов.исх)=4*(sqrt3a^2)/4=sqrt3*a^2`
2) `S_(пов.нов)=4*(sqrt3(2a)^2)/4=4*sqrt3*a^2`
в 4 раза
Ответ: 4
mathege
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

Решение:
Площадь равностороннего треугольника
`S =(sqrt3*a^2)/4`
Объем пирамиды
`V=1/3*S_(осн)*h`
1) `V_1=1/3*(sqrt3*a^2)/4*h`
2) `V_2=1/3*(sqrt3*(2a)^2)/4*2h=8(1/3*(sqrt3*a^2)/4*h)`
в 8 раз
Ответ: 8
mathege
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
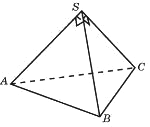
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым, лежащим в этой плоскости
`V=1/3*S_(ASB)*SC=1/3*(3*3)/2*3=4,5`
Ответ: 4,5
mathege
Ребра правильного тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырёх его ребер.
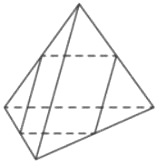
Решение:
Прямая проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной.
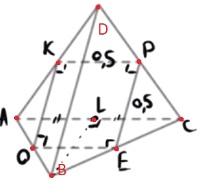
1) BL-проекция BD на пл. основания
BL⊥AC ⇒
BL⊥CE ⇒
наклонная BD⊥CE
2) `S_(кв)=0,5^2=0,25`
Ответ: 0,25
mathege
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 9. Найдите объем пирамиды.
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
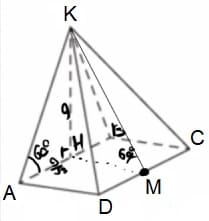
1) ΔKHM:
`tg60=(КH)/(HM)`
`sqrt3=9/(HM)`
`HM=9/sqrt3`
2) ΔAKH:
`tg60=(КH)/(AH)`
`sqrt3=9/(AH)`
`AH=9/sqrt3`
`AB=18/sqrt3`
3) `V=1/3*9/sqrt3*18/sqrt3*9=162`
Ответ: 162
mathege
Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
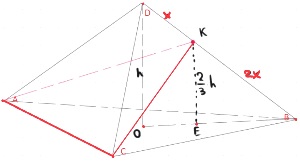
1)`V_(ABCD)=15=1/3*S_(ABC)*h`
`S_(ABC)*h=45`
2)`V_(ABCK)=1/3*S_(ABC)*2/3*h=2/9*45=10`
Ответ: 10
mathege
От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
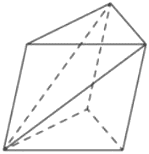
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Объем призмы
`V = S_(осн)*h`
Верхнее основание A1B1C1, нижнее ABC.
1) `V_(пр)=6=S_(ABC)*h`
2) `V_(A_1B_1C_1A)=1/3*S_(ABC)*h=1/3*6=2`
3) `V_(иск)=6-2=4`
Ответ: 4
mathege
Объем параллелепипеда 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 равен 4,5. Найдите объем треугольной пирамиды 𝐴𝐷1𝐶𝐵1.
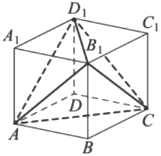
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
`V_(иск)=V_(пар)-V_(ABCB_1)-V_(C C_1D_1B_1)-V_(A_1B_1D_1A)-V_(ABCD)`
1)`V_(пар)=S_(ABCD)*A A_1=4,5`
2)`V_(ABCB_1)=1/3*1/2*S_(ABCD)*A A_1=1/6*4,5=V_(C C_1D_1B_1)=V_(A_1B_1D_1A)=V_(ABCD)`
`4,5-4*1/6*4,5=1/3*4,5=1,5`
Ответ: 1,5
mathege
Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра.
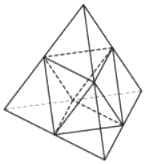
Решение:
1) `S_(тет)=16*S_(ABC)=16*3/4=12`
2) `S_(пов. иск.)=8*S_(ABC)=8*3/4=6`
Ответ: 6
mathege
Объем тетраэдра равен 19. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.

Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
Отношение площадей подобных треугольников
`S_1/S_2=k^2`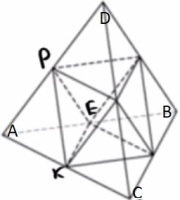
1) `V_(ABCD)=19=1/3*S_(ABC)*h` ⇒ `S_(ABC)*h=57`
2) `V_(APEK)=1/3*S_(AEK)*h/2=1/3*1/4*S_(ABC)*1/2*h=1/24*S_(ABC)*h=1/24*57=19/8`
3) `V_(иск)=19-4*19/8=19-9,5=9,5`
Ответ: 9,5
mathege
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
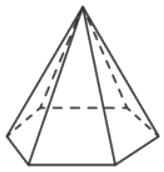
Решение:
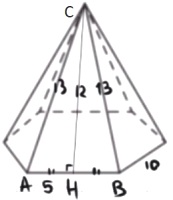
1) `CH=sqrt(13^2-5^2)=12`
2) `S_(ABC)=1/2*10*12=60`
3) `S_(бок.пов.)=6*60=360`
Ответ: 360
mathege
Объем треугольной пирамиды 𝑆𝐴𝐵𝐶, являющейся частью правильной шестиугольной пирамиды 𝑆𝐴𝐵𝐶𝐷𝐸𝐹, равен 1. Найдите объем шестиугольной пирамиды.
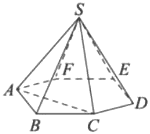
Решение:
Объем пирамиды
`V=1/3*S_(осн)*h`
1) `V_(ABC)=1/3*S_(ABC)*h=1` ⇒ `S_(ABC)*h=3`
2) `V_(шест. пир.)=1/3*S_(шест)*h=1/3*6*S_(ABC)*h=1/3*6*3=6`
Ответ: 6
mathege
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Решение:
Радиус окружности, описанной около равностороннего шестиугольника, равен стороне этого шестиугольника.
Площадь равностороннего шестиугольника
`S = (3sqrt3a^2)/2`
Объем пирамиды
`V=1/3*S_(осн)*h`
S - вершина пирамиды, О - точка, откуда выходит высота пирамиды, A - любая точка вершины шестиугольника у основания, тогда:
1) `AO=2`
2) `SO=sqrt(4^2-2^2)=sqrt12=2sqrt3`
3) `S_(осн)=(3sqrt3*2^2)/2=6sqrt3`
4) `V_(пир)=1/3*6sqrt3*2sqrt3=12`
Ответ: 12
mathege
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45°. Найдите объем пирамиды.

Решение:
Радиус окружности вписанной в равносторонний шестиугольник.
`r=(sqrt3a)/2`
Площадь равностороннего шестиугольника
`S = (3sqrt3a^2)/2`
Объем пирамиды
`V=1/3*S_(осн)*h`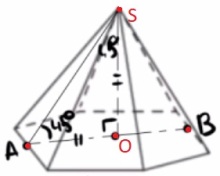
1) ∠ASO=180-90-45=45
ΔASO прямоугольный и равнобедренный
2) `AO=r=sqrt3/2*4=2sqrt3=SO`
3) `S_(осн)=(3sqrt3*4^2)/2=24sqrt3`
4)`V_(пир)=1/3*24sqrt3*2sqrt3=48`
Ответ: 48
mathege
Шар
Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение:
Площадь поверхности шара:
`S=4πR^2`
1) `S_(пов м)=4πR^2`
2) `S_(пов б)=4π(2R)^2=4*4πR^2`
в 4 раза
Ответ: 4
Номер: 4290
Площадь поверхности шара равна 12. Найдите площадь большого круга шара.
Решение:
Площадь круга:
`S=πR^2`
Площадь поверхности шара:
`S=4πR^2`
1) `S_(пов)=12=4πR^2` => `πR^2=3`
2) `S_(круг)=πR^2=3`
Ответ: 3
ЕГЭ 2019
Дано два шара. Радиус первого шара в 13 раз больше радиуса второго. Во сколько раз объём первого шара больше объёма второго?

Решение:
Объем шара:
`V=4/3*πR^3`
1) `V_б=4/3*π(13R)^3=2197*4/3πR^3`
2) `V_м=4/3*πR^3`
в 2197 раз
Ответ: 2197
Номер: 4332
Дано два шара. Диаметр первого шара в 8 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Решение:
Площадь поверхности шара:
`S=4πR^2`
1) `S_(сф.мал)=4πR^2`
2) `S_(сф.мал)=4π(8R)^2=64*4πR^2`
в 64 раза
Ответ: 64
ЕГЭ 2014
Радиусы двух шаров равны 9 и 12. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Решение:
Площадь поверхности шара:
`S=4πR^2`
1) `S_(пов1)=4π*9^2=324π`
2) `S_(пов2)=4π*12^2=576π`
3) `S_(пов3)=324π+576π=900π`
4) `S_(пов3)=900π=4πR_(нов)^2`
`R_(нов)^2=225`
`R_(нов)=15`
Ответ: 15
Номер: 320DAF
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Решение:
Объем шара:
`V=4/3*πR^3`
1) `V_(исх)=4/3*πR^3`
2) `V_(пов)=4/3*π(3R)^3=27*(4/3*πR^3)`
в 27 раз
Ответ: 27
mathege
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Решение:
Объем шара:
`V=4/3*πR^3`
Площадь поверхности шара:
`S=4πR^2`
1) `V_(бол)/V_(мал)=27=(4/3*πR_б^3)/(4/3*πR_м^3)`
`R_б^3/R_м^3=27=3^3`
`R_б/R_м=3`
2) `S_(бол)/S_(мал)=(4π(3R)^2)/(4πR^2)=9`
в 9 раз
Ответ: 9
mathege
Куб и шар
В куб с ребром 3 вписан шар. Найдите объём этого шара, делённый на 𝜋.
Решение:
Объем шара:
`V=4/3*πR^3`
1) `R=3/2`
2) `V=4/3*π(3/2)^3=9/2π=4,5π`
Ответ: 4,5
Номер: 4DADB3
Куб описан около сферы радиуса 2. Найдите объём куба.
Решение:
Объем куба
`V=a^3`
1) `a=2R=2*2=4`
2) `V=4^3=64`
Ответ: 64
Номер: 4479
Шар, объем которого равен 35𝜋, вписан в куб. Найдите объём куба.
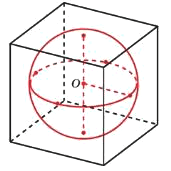
Решение:
Объем куба
`V=a^3`
Объем шара:
`V=4/3*πR^3`
1) `V_ш=4/3*πR^3=35π`
`R^3=35*3/4=105/4`
2) `V_к=(2R)^3=8*R^3=8*105/4=210`
Ответ: 210
mathege, ЕГЭ 2014
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
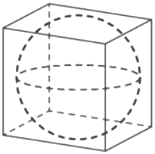
Решение:
Объем куба
`V=a^3`
1) `V_(куб)=216=a^3`
`a^3=6^3`
`a=6`
2) `R=6/2=3`
Ответ: 3
mathege
Куб вписан в шар радиуса √3. Найдите объем куба.
Решение:
Объем куба
`V=a^3`
Диагональ куба
`d=sqrt3*a`
1) `d=2R=2sqrt3`
2) `d=2sqrt3=sqrt3*a`
`a=2`
3) `V=2^3=8`
Ответ: 8
mathege
Параллелепипед и шар
Прямоугольный параллелепипед описан около сферы радиуса 16. Найдите его объём.
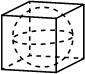
Решение:
Объем прямоугольного параллелепипеда
`V=abh`
`V=32^3=(2^5)^3=2^15=2^10*2^5=1024*32=32768`
Ответ: 32768
Номер: 7D0E46
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

Решение:
`S_(пов)=6*2^2=6*4=24`
Ответ: 24
mathege
Цилиндр и шар
Цилиндр описан около шара. Объём шара равен 50. Найдите объём цилиндра.
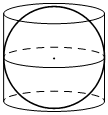
Решение:
Объем шара:
`V=4/3*πR^3`
Объем цилиндра
`V=πR^2h`
1) `V_ш=50=4/3*π*R^3`
`π*R^3=(50*3)/4=75/2`
2) `V_ц=π*R^2*2R=2*πR^3=2*75/2=75`
Ответ: 75
Номер: FCCBC9
Шар, объем которого равен 18, вписан в цилиндр. Найдите объем цилиндра.

Решение:
Объем шара:
`V=4/3*πR^3`
Объем цилиндра
`V=πR^2h`
1) `V_ш=18=4/3*π*R^3`
`π*R^3=(18*3)/4=27/2`
2) `V_ц=π*R^2*2R=2*πR^3=2*27/2=27`
Ответ: 27
2 способ:
Объем шара
`V=4/3*π*r^3`
Объем цилиндра
`V=2π*r*h`
`h=2r`, тогда
`V=π*r^2*2r=2π*r^3`
Объемы относятся как 4/3 и 2, то есть объем цилиндра больше в 2:4/3=1,5 раза
18*1,5=27
Ответ: 27
Номер: 6D5AF2
Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.
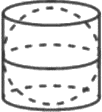
Решение:
Площадь поверхности шара:
`S=4πR^2`
Площадь поверхности цилиндра
`S_ш=2πR^2+2πRh`
1) `S_(пов)=48=4πR^2`
`πR^2=12`
2) `S_(полн. пов. ц.)=2πR^2+2πR*2R=6πR^2=6*12=72`
Ответ: 72
Номер: AFD872
Конус и шар
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса.
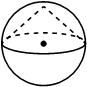
Решение:
Пусть A - точка вершины конуса, B - центр основания конуса, C - любая точка по краю основания конуса (получается BC радиус сферы).
Образующая `AC=sqrt((10sqrt2)^2+(10sqrt2)^2)=sqrt(200+200)=20`
Ответ: 20
Номер: F4AA43
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 50√2. Найдите радиус сферы.

Решение:
Пусть A - точка вершины, B - любая точка на поверхности шара и по краю основания конуса и AC - высота конуса, С - центр шара (получается CB радиус).
ΔABC:
`(50sqrt2)^2=R^2+R^2`
`2500*2=2R^2`
`R^2=2500`
`R=50`
Ответ: 50
Номер: 2A5773
Конус вписан в шар (см. рисунок). Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
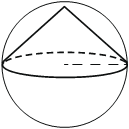
Решение:
Объем шара:
`V=4/3*πR^3`
Объем конуса:
`V=1/3*πR^2h`
1) `V_(кон)=47=1/3*πR^2*R`
`πR^2=141`
2) `V_ш=4/3*141=188`
Ответ: 188
Номер: 857802
Конус и цилиндр
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
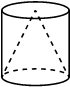
Решение:
Объем конуса:
`V=1/3*πR^2h`
Объем цилиндра
`V=πR^2h`
`V_ц=57*3=171`
Ответ: 171
Номер: 267D7F
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 18. Найдите объем конуса

Решение:
Объем конуса:
`V=1/3*πR^2h`
Объем цилиндра
`V=πR^2h`
1)`V_ц=18=πR^2h`
2)`V_(кон)=1/3*πR^2h=1/3*18=6`
Ответ: 6
2 способ:
Объем цилиндра
Vц=πr2h=18
Объем конуса
Sк=1/3πr2h
То есть, объем конуса в 3 раза меньше цилиндра, в который он вписан
18:3=6
Ответ: 6
Номер: D8F984
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 5√2. Найдите площадь боковой поверхности конуса.
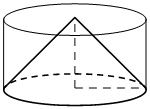
КЭС: 5.4 Тела и поверхности вращения 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение:
Площадь боковой поверхности цилиндра
`S_ц=2πrh`
Площадь поверхности конуса
`S_к=πrl`
`S_ц=2πrh=2πr^2=5sqrt2`
`πr^2=(5sqrt2)/2`
При этом
`l^2=R^2+R^2`
`l=sqrt(2R^2)=Rsqrt2`
`S_к=πR*R sqrt2=πR^2 sqrt2=(5sqrt2*sqrt2)/2=5`
Ответ: 5
Номер: 37164B
Параллелепипед и цилиндр
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра.
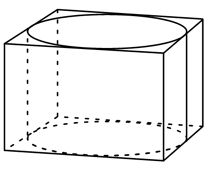
Решение:
Объем прямоугольного параллелепипеда
`V= abh`
`36=6*6*h`
`h=1`
Ответ: 1
Номер: A57713
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.

Решение:
Объем прямоугольного параллелепипеда
`V= abh`
`V=4*4*2=32`
Ответ: 32
Номер: 7BEA25
Призма и цилиндр
В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы равны 2/𝜋. Найдите объём цилиндра, описанного около этой призмы.
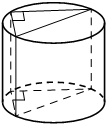
Решение:
Объем цилиндра
`V=πR^2h`
Радиус окружности, описанной около прямоугольного треугольника
`R=c/2`, где с - гипотенуза и диаметр
ΔABC - треугольник в основании призмы
1) ΔABC:
`AB=sqrt(10^2+9^2)=sqrt181`
2) `R=sqrt181/2`
3) `V_ц=π*(sqrt181/2)^2*2/π=181/4*2=90,5`
Ответ: 90,5
Номер: E7964C
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
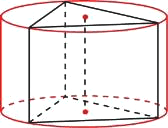
Решение:
Радиус окружности описанной около равностороннего треугольника.
`R=(sqrt3*a)/3`
1) `R=(sqrt3*a)/3=2sqrt3`
`a=2*3=6`
2) `S_(пов. бок.) =3*6*2=36`
Ответ: 36
mathege, ЕГЭ 2017
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 1. Найдите площадь боковой поверхности призмы.
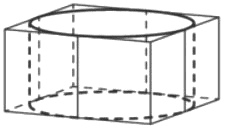
Решение:
`S_(бок)=4*21=8`
Ответ: 8
mathege
Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 12. Площадь боковой поверхности призмы равна 288. Найдите высоту цилиндра.

Решение:
`S_(бок)=288=4*24h`
`h=288/96=3`
Ответ: 3
mathege
В основании прямой призмы лежит квадрат со стороной 2. Боковые рёбра призмы равны 2𝜋. Найдите объём цилиндра, описанного около этой призмы.
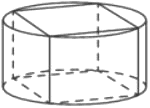
Решение:
Объем цилиндра
`V=πR^2h`
Пусть AB - диагональ прямоугольного основания, С - вершина следующего угла.
1) ΔABC:
`AB=sqrt(2^2+2^2)=sqrt8=2sqrt2`
2) `V_ц=π*sqrt2^2*2/π=4`
Ответ: 4
mathege
Цилиндр вписан в правильную треугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.
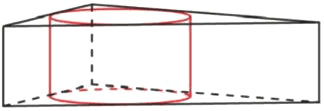
Решение:
Радиус окружности вписанной в равносторонний треугольник.
`r=(sqrt3*a)/6`
1) `sqrt3=(sqrt3*a)/6`
`a=1*6=6`
2) `S_(бок)=3*6*2=36`
Ответ: 36
mathege
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.
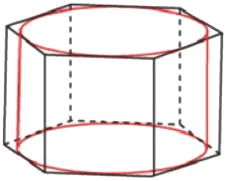
Решение:
Радиус окружности вписанной в равносторонний шестиугольник.
`r=(sqrt3a)/2`
1) `sqrt3=(sqrt3*a)/2`
`a=1*2=2`
2) `S_(бок)=6*2*2=24`
Ответ: 24
mathege

