В 1 части ЕГЭ среди заданий с кратким ответом есть 2 задания на вероятность. Одно из них довольно простое, требуются базовые знания теории вероятностей.
Все прототипы задания ЕГЭ по вероятности (простые) с кратким ответом
В среднем из 900 садовых насосов, поступивших в продажу, 27 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение:
900-27=873 не подтекают
`P=873/900=97/100=0,97`
Ответ: 0,97
Номер: FE2ADA
В сборнике билетов по математике всего 20 билетов, в 16 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам.
Решение:
`P=16/20=8/10=0,8`
Ответ: 0,8
Номер: E31481
В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос про Александра Второго. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос про Александра Второго.
Решение:
`P=37/50=37/50*2/2=74/100=0,74`
Ответ: 0,74
Номер: 89584F
В соревнованиях по толканию ядра участвуют 3 спортсмена из Дании, 6 из Швеции, 4 из Норвегии и 7 из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Норвегии.
Решение:
`P=4/20=2/10=0,2`
Ответ: 0,2
Номер: F805D7
На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 4 прыгуна из Италии и 6 прыгунов из Мексики. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двадцать четвёртым будет выступать прыгун из Мексики.
Решение:
`P=6/25=6/25*4/4=24/100=0,24`
Ответ: 0,24
Номер: 3B1799
В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Решение:
Из Канады: 70-25-17=28
`P=28/720=4/10=0,4`
Ответ: 0,4
Номер: 2EBA48 CA4AFD
На конференцию приехали 2 учёных из Дании, 7 из Польши и 3 из Венгрии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что четвёртым окажется доклад учёного из Венгрии.
Решение:
2+7+3=12 докладчиков
Вероятность быть хоть 1-м, хоть 4-м `1/12`, но так как ученых из Венгрии 3, то вероятность утраивается
`P=3/12=1/4=0,25`
Ответ: 0,25
Номер: 60E929
В фирме такси в наличии 60 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на боках, остальные – жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Решение:
60-27=33 жёлтого цвета с чёрными надписями
`P=33/60=0,55` вероятность, что приедет именно такая машина
Ответ: 0,55
Номер: D295A8
Конкурс исполнителей проводится в 3 дня. Всего заявлено 70 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 28 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?
Решение:
(70-28)/2=21 чел. выступает в третий день
`P=21/70=3/10=0,3`
Ответ: 0,3
Номер: e5D1Ae
Научная конференция проводится в 4 дня. Всего запланировано 80 докладов – первые два дня по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение:
12*2=24 доклада будут в первые два дня
80-24=56 докладов во вторые 2 дня
`56/2=28` докладов в последний день
`P=28/80=7/20=7/20*5/5=35/100=0,35` вероятность попасть на последний день
Ответ: 0,35
Номер: 569129
На олимпиаде по русскому языку 350 участников разместили в трёх аудиториях. В первых двух удалось разместить по 140 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение:
ПО 140, это значит 140 в КАЖДОЙ!
2*140=280 человек разместили в первых двух
`P=280/350=0,8`
`1-0,8=0,2`
Ответ: 0,2
2 способ:
2*140=280 человек разместили в первых двух
350-280=70 человек в третьей (запасной)
`P=70/350=2/10=0,2`
Ответ: 0,2
Номер: 26c68F D9E4B9
Фабрика выпускает сумки. В среднем 6 сумок из 75 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
Решение:
`6/75=0,08` что сумка с дефектом,
`1-0,08=0,92` что сумка без дефекта
Ответ: 0,92
2 способ:
75-6=69 сумок без дефекта
`P=69/75=23/25=23/25*4/4=92/100=0,92`
Ответ: 0,92
Номер: 83C4C1
Фабрика выпускает сумки. В среднем 19 сумок из 160 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых.
Решение:
160-19=141 сумка без дефектов
`P=141/160≈0,881...` до сотых 0,88
Ответ: 0,88
Номер: cF88Fe
Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится 3 сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение:
100+3=103 сумки всего
`P=100/103≈0,9708...` до сотых 0,97
Ответ: 0,97
Номер: C66297
Дима, Марат, Петя, Надя и Света бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Решение:
`P=3/5=3/5*2/2=6/10=0,6` вероятность, что мальчик начнет игру
Ответ: 0,6
Номер: 42eF9e
В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
Решение:
`P=6/8=3/4*25/25=75/100=0,75`
Ответ: 0,75
Номер: 4c1895
В группе туристов 300 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 15 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист В. полетит первым рейсом вертолёта.
Решение:
`P=15/300=5/100=0,05`
Ответ: 0,05
Номер: D3C781
Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 теннисистов, среди которых 7 спортсменов из России, в том числе Анатолий Москвин. Найдите вероятность того, что в первом туре Анатолий Москвин будет играть с каким-либо теннисистом из России.
Решение:
Всего теннисистов, помимо Анатолия Москвина:
76 – 1 = 75
Всего теннисистов из России, помимо Анатолия Москвина:
7 – 1 = 6
Вероятность, что в первом туре Анатолий будет играть с теннисистом из России:
`P=6/75=2/25=2/25*4/4=8/100=0,08`
Ответ: 0,08
Номер: 11C2CE
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.
Решение:
Стрелка между 7 и 1, то есть в секторе из 6 секторов
Вероятность оказаться в 6 секторах из 12 равна
`P=6/12=1/2=0,5`
Ответ: 0,5
Номер: 26190D
Полная вероятность
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°С, равна 0,94. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°С или выше.
Решение:
1-0,94=0,06
Ответ: 0,06
Номер: 4F31D7
Вероятность того, что на тестировании по математике учащийся А. верно решит больше 9 задач, равна 0,63. Вероятность того, что А. верно решит больше 8 задач, равна 0,75. Найдите вероятность того, что А. верно решит ровно 9 задач.
Решение:
Вероятность (P1) решить больше 9 задач ( 10, 11, 12 … задач) = 0,63
Вероятность (P2) решить больше 8 задач (9, 10, 11, 12 … задач) = 0,75
Разница этих вероятностей, в том, что в P2 входит искомая вероятность решения ровно 9 задач, найдём её:
`P_1 – P_2 = 0,75 – 0,63 = 0,12`
Ответ: 0,12
Номер: eFFB3B
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,93. Вероятность того, что окажется меньше 12 пассажиров, равна 0,49. Найдите вероятность того, что число пассажиров будет от 12 до 20.
Решение:
0,93-0,49=0,44
Ответ: 0,44
Номер: 8F393
Группы
В классе 16 учащихся, среди них два друга – Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.
Решение:
Пусть Вадим находится в какой-то группе. Тогда количество людей, которые могут находиться с ним в группе, равно
`16/4 - 1 = 3`
Всего людей кроме Вадима 15.
Благоприятных исходов 3, так как Сергей может быть одним из трех людей, которые в одной группе с Вадимом. Всего исходов 15, так как Сергей может быть любым из 15 оставшихся людей.
Тогда получаем искомую вероятность
`P=3/15=1/5=1/5+2/2=2/10=0,2`
Ответ: 0,2
Номер: e33c5D
В классе 26 семиклассников, среди них два близнеца – Иван и Игорь. Класс случайным образом делят на две группы, по 13 человек в каждой. Найдите вероятность того, что Иван и Игорь окажутся в разных группах.
Решение:
1 гр. И||||||||||||
2 гр. |||||||||||||
Пусть Иван в 1 группе. Поскольку Ивану мы уже выделили место, осталось всего 25 мест, на которых может оказаться Игорь.
Но благоприятным исходом можно назвать только нахождение Игоря на любом из 13 мест во второй группе.
`P=13/25=13/25*4/4=52/100=0,52`
Ответ: 0,52
Номер: 95E728
Монеты
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпала больше раз, чем орёл.
Решение:
ОО
ОР
РО
РР - только тут решка выпала больше раз, чем орел, то есть 1 событие из 4
`P=1/4=0,25`
Ответ: 0,25
Номер: 454B44
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что количество выпавших орлов меньше 2.
Решение:
ООО
ООР
ОРО
ОРР - меньше 2х орлов
РРР - меньше 2х орлов
РРО - меньше 2х орлов
РОР - меньше 2х орлов
РОО
то есть 4 благоприятных события из 8.
`P=4/8=1/2=0,5`
Ответ: 0,5
Номер: 42401C
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение:
ОООО РРРР
ОООР РРРО
ООРО РРОР
ОРОО РОРР
ООРР РРОО
ОРОР РОРО
ОРРО РООР
ОРРР РООО
`P=6/16=3/8=0,375`
Ответ: 0,375
Номер: 08AB19
Кости
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 5 или 6.
Решение:
На игральных костях цифры от 1 до 6. Могут выпасть сочетания:
1 2 3 4 5 6
1 11 21 31 41 51 61
2 12 22 32 42 52 62
3 13 23 33 43 53 63
4 14 24 34 44 54 64
5 15 25 35 45 55 65
6 16 26 36 46 56 66
`P=9/36=1/4=0,25`
Ответ: 0,25
Номер: 19880B
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.
Решение:
1 2 3 4 5 6
1 11 21 31 41 51 61
2 12 22 32 42 52 62
3 13 23 33 43 53 63
4 14 24 34 44 54 64
5 15 25 35 45 55 65
6 16 26 36 46 56 66
`P=9/36=1/4=0,25`
Ответ: 0,25
Номер: 784B7D
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 7. Результат округлите до тысячных.
Решение:
11 21 31 41 51 61
12 22 32 42 52 62
13 23 33 43 53 63
14 24 34 44 54 64
15 25 35 45 55 65
16 26 36 46 56 66
`P=6/36=1/6≈0,1666...` до сотых 0,167
Ответ: 0,167
Номер: 4c90B4
mathege
При изготовлении подшипников диаметром 68 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,968. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 67,99 мм, или больше, чем 68,01 мм.
Решение:
1-0,968=0,032
Ответ: 0,032
mathege
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Решение:
Садим первую девочку на любой стул.
Осталось 4 стула, на которые можно посадить вторую девочку. Но благоприятный исход только тогда, когда вторая девочка сидит рядом с первой, а это ближних 2 стула.
`P=2/4=1/2=0,5`
Ответ: 0,5
mathege
В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орел выпадет ровно 3 раза.
Решение:
`P=10/32=5/16=0,3125`
Ответ: 0,3125
mathege
На рок-фестивале выступают группы – по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Китая будет выступать после группы из Вьетнама и после группы из Канады? Результат округлите до сотых.
Решение:
... Ки В Ка ...
... Ки Ка В ...
... Ка Ки В ...
... Ка В Ки ...
... В Ки Ка ...
... В Ка Ки ...
`P=2/6=1/3≈0,333` до сотых 0,33
Ответ: 0,33
mathege
При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Решение:
Всего насосов 2982+18=3000
`P=18/3000=6/1000=0,006`
Ответ: 0,006
mathege
Из множества натуральных чисел от 58 до 82 наудачу выбирают одно число. Какова вероятность того, что оно делится на 6?
Решение:
От 58 до 82, значит включая эти числа!
82-58+1=25 чисел
На 6 делятся: 60 66 72 78 - то есть 4 числа
`P=4/25=4/25*4/4=16/100=0,16`
Ответ: 0,16
mathege
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу 𝐷.
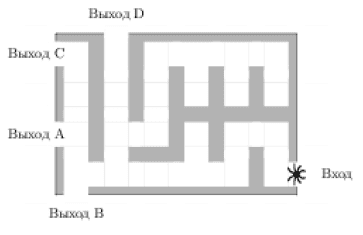
Решение:
`1/2*1/2*1/2=0,125`
Ответ: 0,125
mathege
Какова вероятность того, что последние две цифры случайного телефонного номера различны?
Решение:
Всего чисел 10: 0 1 2 3 4...9
Одну любую цифру ставим на предпоследнее место, тогда благоприятным исходом можно считать любую из оставшихся 9-ти цифр на последнем месте, а неблагоприятным - еще одну ту же цифру.
`P=9/10=0,9`
Ответ: 0,9
mathege
Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,093. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 97 штук. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение:
0,093 - вероятность поступления в гарантийный ремонт
`97/1000=0,097`- частота поломки в некотором городе
0,097 - 0,093 = 0,004
Ответ: 0,004
mathege

