Одна из линеек ЕГЭ по профильной математике проверяет умение работать с заданиями по теории вероятности повышенной сложности. Мы собрали все прототипы этой линейки.
Все прототипы задания ЕГЭ по вероятности (сложные) с кратким ответом
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
0,55
Так как события самодостаточные и могут выпасть в один момент, то вероятность проявления одного из них равна сумме вероятностей каждого из них
0,2+0,35=0,55
Ответ: 0,55
Номер: 5e924B
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
0,16
Чтобы шахматист А. выиграл оба раза, он должен выиграть у шахматиста Б. играя белыми и играя черными. Имеем два независимых события:
А: шахматист А. играет белыми и выигрывает у Б;
B: шахматист А. играет черными и выигрывает у Б.
Вероятность события A равна P(A), а вероятность события B равна P(B). Следовательно, вероятность того, что А. выиграет оба раза, равна P = P(A)*P(B)
0,32*0,5= 0,16, что выиграет второй раз
Ответ: 0,16
Номер: B5BD2F
Стрелок стреляет по одному разу в каждую из четырёх мишеней. Вероятность попадания в мишень при каждом отдельном выстреле равна 0,9. Найдите вероятность того, что стрелок попадёт в первую мишень и не попадёт в три последние.
Решение:
1) 1 `{(P (попасть) = 0.9),(P (промахнуться) = 0.1):}`
2) V Х Х Х
P = 0,9 • 0,1 • 0,1 • 0,1 = 0,0009
Ответ: 0,0009
Номер: F3F0DF
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,8. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
0,488
0,8*0,8*0,8=0,512 вероятность перегорания всех ламп
1-0,512=0,488 вероятность, что не перегорит хотя бы одна
Ответ: 0,488
Номер: 0ECDD4
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение:
0,33
1-0,3-0,3=0,4 ничья
P(выиграть)=0,3
P(проиграть)=0,3 }1
P(ничья)=0,4
Нас устроят варианты
выиграть - ничья 4 очка
ничья - выиграть 4 очка
выиграть - выиграть 6 очков
0,3*0,4=0,12
0,4*0,3=0,12
0,3*0,3=0,09
Теперь, так как нас устраивает любое событие, мы их складываем
0,12+0,12+0,09=0,33
Ответ: 0,33
Номер: 21DD4A
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение:
0,11
0,93-0,82=0,11
Ответ: 0,11
Номер: CA9F71
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,96. Вероятность того, что масса окажется больше 790 г, равна 0,82. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Решение:
0,78
1-0,82=0,18 - вероятность, когда хлеб меньше 790 г.
В итоге вероятность 0,96 включает в себя вероятность 0,18, значит
0,96-0,18=0,78
Ответ: 0,78
Номер: 66F056
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,06. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Решение:
0,069
0,01*0,96=0,0096 - это вероятность на выходе не только произвести, но и выявить неисправную батарейку
1-0,01=0,99 - это вероятность выпуска исправных батареек
0,99*0,06=0,0594 вероятность, что система забракует исправную батарейку
В итоге брак будет складываться из двух событий
0,0096+0,0594=0,069
Ответ: 0,069
Номер: 91D905
По отзывам покупателей Василий Васильевич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,93. Вероятность того, что этот товар доставят из магазина Б, равна 0,94. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение:
P(A не доставит) = 0,07
P(Б не доставит) = 0,06
0,07 * 0,06 = 0,0042
Ответ: 0,0042
ЕГЭ 2014
В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение:
1 способ
x чел `{(0.48*x - мужчины),(0.52*x - женщины):}`
0,126x - пенсионера.
0,15-0,52*x=0,078x - женщины пенсионеры
0,126x-0,078x = 0,048x- мужчины пенсионеры
`P=(0,048x)/(0,48x)=0,1`
2 способ
1000 чел `{(480 - мужчины),(520 - женщины):}`
126 - пенсионеры
0,15*520=78 - женщины пенсионеры
126-78=48 - мужчины пенсионеры
`P=48/480=0,1`
Ответ: 0,1
Демоверсия 2022
Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,5 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не меньше 0,7?
Решение:
2
1 способ
Вероятность промаха при 1 выстреле равна 1-0,5=0,5
При 2 выстреле вероятность промаха P=(1-0,5)2=0,25 то есть 1-P=0,75 вероятность попадания
2 способ
Вероятность попадания на первый раз 0,5.
Вероятность для второго выстрела как для второго события, когда первый раз не попал, а второй попал 0,5*0,5=0,25.
В принципе, эта вероятность действительна для любого второго события - выстрела, то есть не попасть будет такая же вероятность 0,5 не попал в первый раз и 0,5 не попал во второй 0,5*0,5=0,25
В итоге получается, что 0,5 первое событие + 0,25 второе = 0,75 вероятность наступления второго события или можно вывести универсальную формулу
1+x12+x23+x34+... гдe x c индексом номер события по порядку.
Ответ: 2
Номер: 30D3F2
На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 65% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Решение:
1 способ
х тарелок `{(0.9x - идеальные),(0.1x - с дефектом):}`
0,65*0,1х - тарелки с обнаруженным дефектом
0,35*0,1х - тарелки с дефектом которые не обнаружили
`P = (0,9x)/(0,9x+0,035x)=(0,9x)/(0,935x)≈0,96`
2 способ
х тарелок `{(900 - идеальные),(100 - с дефектом):}`
65 - тарелки с обнаруженным дефектом
35 - тарелки с дефектом которые не обнаружили
`P = 900/935≈0,96`
Ответ: 0,96
mathege
В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
Решение:
0,027
Скажем, заходит покупатель в магазин, при этом вероятность того, что будет занят один продавец 0,3 - из условия, а вероятность, что он зайдет и занято два уже уменьшается согласно принципу, что и так к нему особо не подходили (имеется в виду, что любой из продавцов мог стать первым занятым с клиентом), а именно 0,3 всех посетителей хотели проконсультироваться, а значит ко второму вероятность попасть еще меньше, ибо выше вероятность, что попадешь на первого. А может ты зашел и тебе продавец не нужен с той же вероятностью что не нужен первый, но блин он уже каким то чудом занят, с вероятностью 0,3, а значит выберешь второго тоже с вероятностью 0,3 из события, которое произошло с вероятностью 0,3. Тогда получается 0,3*0,3=0,09 что второго займут. Ну и тогда для третьего...
0,3*0,3*0,3=0,027
Ответ: 0,027
mathege
Вероятность того, что батарейка бракованная, равна 0,04. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
1 `{(P (брак) = 0.04),(P (хор) = 0.96):}`
`0,96*0,96=9216/10000=0,9216`
Ответ: 0,9216
mathege
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение:
1 `{(P (попасть) = 0.7),(P (промахнуться) = 0.3):}`
v v x x
0,7*0,7*0,3*0,3=0,49*0,09=0,0441≈0,04
Ответ: 0,04
mathege
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
1 способ
P(отдельный автомат сломался) = 0,05
P(оба сломались) = 0,05*0,05=0,0025 } 1
P(хотя бы 1 исправен) = 1 - 0,0025=0,9975
2 способ
Вероятности по двум автоматам.
PP=0,95-0,95=0,0025
РС=0,95*0,05=0,0475
СР=0,05*0,95=0,0475 } 1
СС=0,05*0,05=0,0025
1-0,0025 = 0,9975
Ответ: 0,9975
mathege
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
P(бракованное стекло с 1 фабрики)=0,25*0,04=0,010
P(бракованное стекло со 2 фабрики)=0,75*0,02=0,015
0,010+0,015=0,025
Ответ: 0,025
mathege
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 77% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Решение:
P(болеет и болезнь выявлена)=0,77*0,9
P(здоров и произошла ошибка)=0,23*0,02
0,77*0,9+0,23*0,02=0,6930+0,0046=0,6976 выявлено больных
Ответ: 0,6976
mathege
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 70% яиц высшей категории. Всего высшую категорию получает 65% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение:
P(из 1 хоз. и высшей категории)=0,6x
P(из 2 хоз. и высшей категории)=(1-x)*0,7
0,6x+(1-x)*0,7=0,65
0,6x+0,7-0,7x=0,65
0,05=0,1x
0,5=x
Ответ: 0,5
mathege
Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать на ЕГЭ не менее 79 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на специальность «Таможенное дело», нужно набрать не менее 79 баллов по каждому из трёх предметов – математика, русский язык и обществознание.
Вероятность того, что абитуриент Б. получит не менее 79 баллов по математике, равна 0,9, по русскому языку – 0,7, по иностранному языку – 0,8 и по обществознанию – 0,9.
Найдите вероятность того, что Б. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение:
3 варианта поступления:
Поступить на Переводчик
Не поступить на Таможенное дело
0,9*0,7*0,8*0,1
Поступить на Переводчик
Поступить на Таможенное дело
0,9*0,7*0,8*0,9
Не поступить на Переводчик
Поступить на Таможенное дело
0,9*0,7*0,9*0,2
0,63*(0,08+0,72+0,18)=0,63*0,98=0,6174
Ответ: 0,6174
mathege
Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент», нужно набрать не менее 67 баллов по каждому из трёх предметов – математика, русский язык и обществознание.
Вероятность того, что абитуриент Р. получит не менее 67 баллов по математике, равна 0,5, по русскому языку – 0,6, по иностранному языку – 0,9 и по обществознанию – 0,7.
Найдите вероятность того, что Р. сможет поступить на одну из двух упомянутых специальностей.
Решение:
2 варианта поступления
Поступить на Переводчик
Не поступить на Менеджмент
0,5*0,6*0,9*0,3
Поступить на Менеджмент
Не поступить на Переводчик
0,5*0,6*0,7*0,1
0,3*(0,27-0,07)=0,34*0,3=0,102
Ответ: 0,102
mathege
Телефон передаёт SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.
Решение:
P(передать с первой попытки) = 0,4
P(передать со второй попытки) = (1-0,4)*0,4=0,6*0,4=0,24
0,4+0,24=0,64
Ответ: 0,64
mathege
Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?
Решение:
P(получить новую принцессу) = `8/10`
P(получить принцессу, которая была) = `2/10`
P(понадобиться 2 шоколадных яйца) = `2/10*8/10=0,160`
P(понадобиться 3 шоколадных яйца) = `2/10*2/10*8/10=0,032`
0,032+0,16=0,192
Ответ: 0,192
mathege
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,4. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,9?
Решение:
Р(уничтожения)≥0,9
Р(уцелеть)≤0,1
Р(уцелеть при первом выстреле)=0,7
Р(уцелеть при последующих выстрелах)=0,6
| Выстрел | Вероятность уцелеть |
| 1 | 0,7 |
| 2 | 0,7*0,6=0,42 |
| 3 | 0,7*0,6*0,6=0,252 |
| 4 | 0,7*0,6*0,6*0,6=0,1512 |
| 5 | 0,7*0,6*0,6*0,6*0,6=0,09072 |
Ответ: 5
mathege
Монеты
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Протор», «Ротор» и «Мотор». Найдите вероятность того, что «Стартер» будет начинать только вторую и последнюю игры.
Решение:
Варианты:
В - вторая
П - первая
ВВВ
ВВП
ВПВ
ВПП
ППП
ППВ
ПВП
ПВВ
`Р = 1/8=0,125`
Ответ: 0,125
ЕГЭ 2019
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом все три раза.
Решение:
0,125
ВВВ
ВВП
ВПВ
ВПП
ППП
ППВ
ПВП
ПВВ
`Р = 1/8=0,125`
Ответ: 0,125
2 способ:
Вероятность `1/2=0,5` для каждого броска. При этом каждый последующий раз должен быть 0,5 от предыдущего, тогда:
0,5*0,5*0,5 = 0,125
Ответ: 0,125
Номер: A203F4
Кости
Игральную кость бросили два раза. Известно, что шесть очков не выпало ни разу. Найдите при этом условии вероятность события «сумма очков равна 8».
Решение:
0,12
На кубике 6 граней, 6 не выпадала.
Возможные вариации:
4+4
5+3
3+5
То есть
`1/5=0,2` что выпадет 4
Тоже самое для второго ряда событий
`1/5=0,2` что выпадет 4
В итоге вероятность такого исхода 0,2*0,2=0,04
По факту у нас три аналогичные ситуации с цифрами, смотрите выше, а значит
0,04*3=0,12
Ответ: 0,12
2 способ - таблица
11 21 31 41 51 61
12 22 32 42 52 62
13 23 33 43 53 63
14 24 34 44 54 64
15 25 35 45 55 65
16 26 36 46 56 66
`P=3/25=12/100=0,12`
Ответ: 0,12
Номер: 97B50F
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Решение:
Возможные варианты:
411
141
114
321
312
132
123
213
231
222
6 раз из 10, получается:
`P=6/10=0,6`
Ответ: 0,6
Демоверсия 2022
Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.
Решение:
Варианты бросков с суммой 8.
26
35
44
53
62
Ии 5 раз 1 удовлетворяющий случай.
`P=1/5=0,2`
Ответ: 0,2
mathege
При двукратном бросании игральной кости в сумме выпало 9 очков. Какова вероятность того, что хотя бы раз выпало 5 очков?
Решение:
Варианты бросков с суммой 9.
36
45
54
63
2 раза из 4, получается:
`P=2/4=0,5`
Ответ: 0,5
mathege
Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали второй кубик?
Решение:
| Обычный кубик | Нет чётных |
| 35 53 2 варианта |
3(1) 5(1) 3(1) 5(1) 3(2) 5(1) 3(2) 5(2) 3(1) 5(1) 3(1) 5(2) 3(2) 5(1) 3(2) 5(2) 8 вариантов |
`P= 8/10=0,8`
Ответ: 0,8
mathege
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Решение:
При 1 броске, варианты:
1
2
3
4
5
6
При 2 броске, варианты:
если выбросили 1 в 1-м
11
12
если выбросили 2 в 1-м
21
остальные будут давать больше
При 3 броске, варианты:
если в 1 и 2 броске по 1
111
(бросков может быть 1, 2 или 3 не более!)
То есть вероятность второго броска будет определяться как возможность его совершить при успешном первом, но на третий нам как бы и не надо!
Итак, в первом броске нас устраивают только очки: 1,2,3, если будет больше то бросать перестанем
P1 Во-втором броске, если при первом броске выпало 1, то нас устраивает 3,4,5,6, чтобы перестать бросать дальше
P2 Во-втором броске, если при первом броске выпало 2, то нас устраивает 2,3,4,5,6
P3 Во-втором броске, если при первом броске выпало 3, то нас устраивает 1,2,3,4,5,6
`P=1/6∗4/6+1/6∗5/6+1/6∗6/6 = 0,416...≈ 0,42`
Ответ: 0,42
mathege
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Решение:
А – сумма всех выпавших очков равна 4;
В – сделан 1 бросок;
Р(АВ) – 1-м броском, выпало 4 очка;
Р(А) – все случаи, когда сумма всех выпавших очков рана 4;
Р(В|А) – вероятность того, что был сделан 1-н бросок, при условии что выпало 4 очка, находится по формуле условной вероятности:
P(B|A)=P(AB)/P(A)
Вероятность того, что 4 очка выпало при 1-м броске:
Р(АВ)=1/6
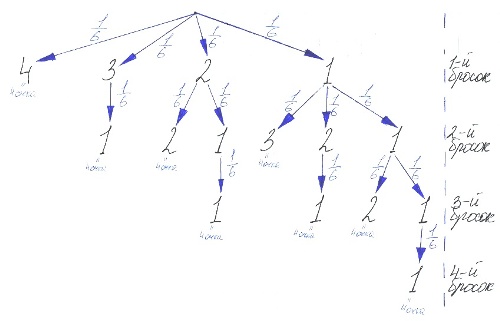
Изобразим все случаи деревом вариантов при которых выпало 4 очка:
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4.
Посчитаем чему равна эта вероятность:
`Р(А)=1/6+(1/6)^2+(1/6)^2+(1/6)^3+(1/6)^2+(1/6)^3+(1/6)^3+(1/6)^4=343/(6^4)`
Подставим найденные значения в формулу (1) и найдём вероятность того, что был сделан 1 бросок:
`P(B|A)=(P(AB))/(P(A))=1/6:343/6^4=1/6*(6^4)/343=(6^3)/343=216/343≈0,629 ≈ 0,63`
Ответ: 0,63
mathege
В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Решение:
2 варианта
Сначала 5
Потом 6
`Р = 1/6*1/6=1/36`
Сначала 6
Потом 5
`Р = 1/6*1/6=1/36`
Р(выпадет комбинация 5 и 6) = `1/36+1/36=2/36=1/18`
Р(не выпадет комбинация 5 и 6) =`1-1/18=17/18`
Р(за две попытки комбинация 5 и 6 не выпала) = `17/18*17/18=289/324`
Р(хотя бы за 1 попытку выпала комбинация 5 и 6) = `1-289/324=35/324≈0,11`
Ответ: 0,11
mathege
Полная вероятность
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,03. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.
Решение:
0,83
Сначала найдем вероятность, что кофе закончится хотя бы в одном автомате. Имеем два события:
А: кофе закончилось в первом автомате;
B: кофе закончилось во втором автомате;
A∙B: кофе закончилось в обоих автоматах.
Вероятность этих событий равна P(A)=P(B)=0,1, P(AB)=0,03. Вероятность суммы событий A+B (кофе закончилось или в первом или во втором автомате или в обоих вместе), равна:
P(A+B)=P(A)+P(B)-P(AB)
P(A+B)=0,1+0,1-0,03=0,17
Тогда обратная вероятность
1-P(A+B)=1-0,17=0,83
будет означать, что кофе осталось в обоих автоматах.
Ответ: 0,83
Номер: 346547
Ящики/коробки
В коробке 11 синих, 6 красных и 8 зелёных фломастеров. Случайным образом выбирают два фломастера. Найдите вероятность того, что окажутся выбраны один синий и один красный фломастеры.
Решение:
Варианты:
Сначала синий
Потом красный
`11/25*6/24=11/100`
Сначала красный
Потом синий
`6/25*11/24=11/100`
`11/100+11/100=0,22`
Ответ: 0,22
Номер: 27C71D
В ящике четыре красных и два синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счёту?
Решение:
ККККСС
P(что вытащат К первым)=4/6
P(что вытащат К вторым)=3/5
P(что вытащат С третьим)=2/4
`4/6*3/5*2/4=1/2=0,2`
Ответ: 0,2
mathege

