Все прототипы заданий из первой части ЕГЭ по профильной математике, в которых нужно найти результат, подставив известное в формулу.
Линейные
Некоторая компания продает свою продукцию по цене 𝑝=600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют 𝜈=400 руб., постоянные расходы предприятия 𝑓=600000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле `π(q)=q(p−v)−f`. Определите месячный объём производства 𝑞 (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 500000 руб.
Решение:
`500000=q(600-400)-600000`
`1100000=q*200`
`q = 1100000/200=5500`
Ответ: 5500
Номер: mathege
Квадратные
Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону `φ=ωt + (βt^2)/2`, где t — время в минутах, прошедшее после начала работы лебёдки, ω=50 град./мин — начальная угловая скорость вращения катушки, а β=4 град./мин2 — угловое ускорение, с которым наматывается кабель. Определите время, прошедшее после начала работы лебёдки, если известно, что за это время угол намотки 𝜑 достиг 2500°. Ответ дайте в минутах.
Решение:
`2500=50t+4/2*t^2`
`2t^2+50t-2500=0` |:2
`t^2+25t-1250=0`
`D=625+5000=5625=75^2`
`t = (-25±75)/2=25`
Ответ: 25
Номер: 5115
Автомобиль, движущийся со скоростью v0=24 м/с , начал торможение с постоянным ускорением a=3 м/с2 . За t секунд после начала торможения он прошёл путь `S=v_0t−(at^2)/2` (м). Определите время, прошедшее с момента начала торможения, если известно, что за это время автомобиль проехал 90 метров. Ответ дайте в секундах.
Решение:
`S=v_0t−(at^2)/2`
`90=24t−(3t^2)/2`
Обе части умножим на 2 и разделим на 3
`60=16t - t^2`
`t^2-16t +60 = 0`
`D = 256-4*1*60=16`
`t_1=(16+4)/2=10`
`t_2=(16-4)/2=6`
Берем меньшее значение, так как остановившись через 6 секунд нельзя это сделать повторно в 10 секунд.
Ответ: 6
Номер: 8027FE (старый 5077)
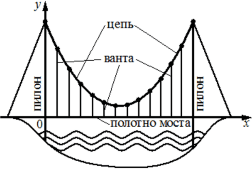
На рисунке изображена схема моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
Введём систему координат: ось 𝑂𝑦 направим вертикально вверх вдоль одного из пилонов, а ось 𝑂𝑥 направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой
`y=0,0043x^2−0,74x+35`, где 𝑥 и 𝑦 измеряются в метрах. Найдите длину ванты, расположенной в 70 метрах от пилона. Ответ дайте в метрах.
Решение:
`y=43/1000*70*70-74/100*70+35`
`y=2107/100-518/10+35`
`y =21,07-51,8+35`
`y=56,07-51,08=4,27`
Ответ: 4,27
Номер: 7D7F1D
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону `H(t)=a t^2+b t+H_0`, где `H_0=3` м — начальный уровень воды, `a=1/768` м/`мин^2` и `b=−1/8` м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
Решение:
`O = 1/768*t^2-1/8t+3` |*768
`t^2-96t+2304=0`
`t-2*48t+48^2=0`
`(t-48)^2=0`
`t=48`
Ответ: 48
Номер: E4E32E
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону
`H(t)=H_0−sqrt(2gH_0) kt+g/2 k^2t^2`, где 𝑡 — время в секундах, прошедшее с момента открытия крана, `H_0=5` м — начальная высота столба воды, `k=1/200` — отношение площадей поперечных сечений крана и бака, а 𝑔 — ускорение свободного падения (считайте 𝑔=10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
Решение:
`1/4*5=5-sqrt(2*10*5)*1/200*t+10/2*1/200*1/200*t^2`
`1/8000*t^2-1/20*t+15/4=0` |*8000
`t^2-400t+30000=0`
`D=160000-120000=40000=200^2`
`t=(400±200)/2`
`t_1=300` (исключаем, так как через 100 с будет выполнено условие задачи)
`t_2=100`
Ответ: 100
Номер: mathege
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой 𝑚=4 кг и радиуса 𝑅=10 см, и двух боковых с массами 𝑀=2 кг и с радиусами 𝑅+ℎ. При этом момент инерции катушки относительно оси вращения, выражаемый в кг∙см2, даeтся формулой `I=((m+2M)R^2)/2+M(2Rh+h^2)`. При каком максимальном значении ℎ момент инерции катушки не превышает предельного значения 1000 кг∙см2? Ответ выразите в сантиметрах.
Решение:
`I≤1000`
`((m+2M)*R^2)/2+M(2Rh+h^2)≤1000`
`(8*100)/2+2(20h*h^2)-1000≤0`
`2h^2+40h-600≤0` |:2
`h^2+20h-300≤0`
`h_1=-30`
`h_2=10`
Нарисуем область получившихся значений в виде координаты с показаниями:
+ - +
-30 10
нас интересует интервал с минусовыми значениями, где макс будет 10
Ответ: 10
Номер: mathege
Мотоциклист, движущийся по городу со скоростью 𝜈0=57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 𝑎=12 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением `S=v_0t+(at^2)/2`. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ дайте в минутах.
Решение:
`S≤30`
`V_0*t+at^2/2≤30`
`57*t+12/2*t^2-30≤0`
`6t^2+57t-30≤0` |:3
`2t^2+19t-10≤0`
`D=361+80=21^2`
`t=(-19±21)/4` (само собой, отрицательное значение корня нас не интересует)
`t=2/4=1/2`
`60*0,5=30` мин
+ - +
-10 1/2
Ответ: 30
Номер: mathege
Высота над землёй подброшенного вверх мяча меняется по закону `h(t)=2+13 t−5 t^2`, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?
Решение:
`h≥8`
`2+13t-5t^2≥8`
`-5t^2+13t-6≥0`
`D=169-120=7^2`
`t=(-13±7)/(-10)`
`t_1=2`
`t_2=0,6`
`2-0,6=1,4` c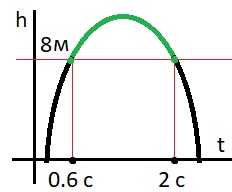
Ответ: 1,4
Номер: D9AE4D
Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой `y=ax^2+bx`, где `a=−1/100` м−1, `b=4/5` — постоянные параметры, 𝑥 (м) — смещение камня по горизонтали, 𝑦 (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Решение:
14+1=15 м минимальная высота полета камней.
`y≥15`
`ax^2+bx≥15`
`-1/100*x^2+4/5x-15≥0` |*(-100)
`x^2-80x+1500≤0`
`D=6400-4*1*1500=400=20^2`
`x=(80±20)/2`
`x_1=30`
`x_2=50`
+ (- выше 1 м) +
30 50
то есть максимально возможное расстояние 50 м
Ответ: 50
Номер: mathege
Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле `T(t)=T_0+bt+at^2`, где t — время в минутах, T0=1300 К, `a=−14/3` К/мин2, b=98 К/мин. Известно, что при температуре нагревателя свыше 1720 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Решение:
`T≤1720`
`T_0+b*t+a*t^2≤1720`
`1300+98*t-14/3*t^2-1720≤0`
`-14/3*t^2+98t-420≤0` |*3 : 14
`-t^2+21t-90≤0`
`D=441-360=9^2`
`t=(-21±9)/-2`
- (+ сгорит) -
6 15
Берем наименьшее время в нашем случае, так как область "сгорит" нам не подходит, ведь там уже прибор может стать неисправным.
Ответ: 6
Номер: F88F7B
Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: `T(t)=T_0 +b t+a t^2`, где t — время (в мин.), T0 =680 К, a=− 16 К / мин2, b=224 К / мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
Решение:
`T≤1400`
`T_0+b*t+a*t^2≤1400`
`680+224t-16t^2-1400≤0`
`-16t^2+224*t-720≤0`
`-t^2+14t-45≤0`
`D=196-180=4^2`
`t=(-14±4)/-2`
- (+ сгорит) -
5 9
Берем наименьшее время в нашем случае, так как область сгорит нам не подходит, ведь там уже прибор может стать неисправным.
Ответ: 5
Номер: 3E9A45
Рациональные
К источнику с ЭДС ε=180 В и внутренним сопротивлением r=1 Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле `U=(εR)/(R+r)`. При каком значении сопротивления нагрузки напряжение на ней будет равно 170 В ? Ответ дайте в омах.
Решение:
`170/1=(180R)/(R+1)`
`17*(R+1)=18R`
`17R+17=18R`
`R=17`Ом
Ответ: 17
Номер: 5BAD91 (старый 5153)
К источнику с ЭДС 𝜀=115 В и внутренним сопротивлением 𝑟=0,6 Ом, хотят подключить нагрузку с сопротивлением 𝑅 Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой `U=(εR)/(R+r)`. При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 100 В? Ответ выразите в омах.
Решение:
`U≥100`
`(ε*R)/(R+r)≥100`
`(115R)/(R+0,6)-100/1≥0`
`(115R-100R-60)/(R+0,6)≥0`
`(15R-60)/(R+0,6)≥0`
+ - +
-0.6 4
Само собой отрицательное значение сопротивления не берем, значит 4 Ома
Ответ: 4
Номер: ЕГЭ 2019
Сила тока в цепи I (в А) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: `I=U/R`, где U — напряжение (в В), R — сопротивление электроприбора (в Ом). В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое наименьшее сопротивление может быть у электроприбора, подключаемого к сети в 220 В, чтобы сеть продолжала работать. Ответ дайте в омах.
Решение:
`I=U/R`
`R=U/I`
Максимально возможная сила тока 2,5 А, а поскольку сопротивление обратно пропорционально силе тока, оно будет при этом значении минимальным. Найдем R
`R=220/(2,5)`
`R = 88` Ом
Ответ: 88
Чисто математический вариант решения:
`I≤2,5`
`U/R≤2,5`
`220/R-5/2≤0`
`(440-5R)/2R≤0`
- + -![]()
0 88
Ответ: 88
Номер: 06534C
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле `f=f_0 ⋅ (c+u)/(c−v)`, где f0 =170 Гц — частота исходного сигнала, c — скорость распространения сигнала в среде (в м/с), а u=2 м /с и v=17 м /с — скорости приёмника и источника относительно среды. При какой скорости c распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.
Решение:
`180=170(c+2)/(c-17)`
`(c+2)/(c-17)=18/17`
`18(c-17)=17(c+2)`
`18c-18*17=17c+2*17`
`18c-17c=2*17+18*17`
`c=17*20=340`
Ответ: 340
Номер: 9602C9
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f0=170 Гц и определяется следующим выражением: `f=f_0 ⋅ (c+u)/(c−v)` (Гц), где c — скорость распространения сигнала в среде (в м/с), а u=12 м/с и v=6 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 180 Гц?
Решение:
`f≥180`
`f=f_0 * (c+u)/(c−v)≥180`
`f_0*(c+12)/(c-6)≥180`
`170*(c+12)/(c-6)≥180` |:17
`(c+12)/(c-6)≥18/17`
`(c+12)/(c-6)-18/17≥0`
`(17c+204-18c+108)/(17(c-6))≥0`
`(-c+312)/(17(c-6))≥0`
Найдем нули функции, приравняв числитель и знаменатель к 0:
`17(c-6)=0`
`с_1=6` (выколотая точка, так как знаменатель обращается в 0)
`-c+312=0`
`с_2=312`
Строим интервал, удовлетворяющий условиям
- + -![]()
-6 312
Берем максимальное значение.
Ответ: 312
Номер: 9685F7
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 494 МГц. Скорость погружения батискафа v вычисляется по формуле `v=c⋅ (f−f_0)/(f+f_0)`, где с=1500 м /с — скорость звука в воде, f0 — частота испускаемых импульсов, f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 18 м/с.
Решение:
`18=1500*(f-494)/(f+494)`
`(f-494)/(f+494)=18/1500`
`(f-494)/(f+494)=3/250`
`3f+3*494=250f-250*494`
`250*494+3*494=250f-3f`
`494*(250+3)=247*f`
`f=(494*253)/247=506`
Ответ: 506
Номер: E819AD
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 217 МГц. Скорость погружения батискафа, выражаемая в м/с, определяется по формуле `v=c⋅ (f−f_0)/(f+f_0)`, где c=1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 12 м/с. Ответ выразите в МГц.
Решение:
`V≤12`
`C*(f-f_0)/(f+f_0)≤12`
`1500*(f-217)/(f+217)≤12` | :1500
`(f-217)/(f+217)≤12/1500`
`(f-217)/(f+217)≤1/125`
`(f-217)/(f+217)-1/125≤0`
`(125f-125*217-f+1*217)/(125*(f+217))≤0`
`(124f-126*217)/(125*(f+217))≤0`
Найдем нули функции
`(125*(f+217))=0` при `f=-217`
`124f-126*217=0`
`124f=126*217`
`f=126*217/124=31,5*7=220,5`
Строим интервал, удовлетворяющий условиям
+ - +![]()
-217 220,5
Ответ: 220,5
Номер: E44604
В розетку электросети подключена электрическая духовка, сопротивление которой составляет R1 =60 Ом. Параллельно с ней в розетку предполагается подключить электрообогреватель, сопротивление которого R2 (в Ом). При параллельном соединении двух электроприборов с сопротивлениями R1 и R2 их общее сопротивление вычисляется по формуле `Rобщ=(R_1R_2)/(R_1+R_2)`. Для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 10 Ом. Определите наименьшее возможное сопротивление R2 электрообогревателя. Ответ дайте в омах.
Решение:
`R_(общ)≥10`
`(R_1*R_2)/(R_1+R_2)≥10`
`(R_1*R_2)/(R_1+R_2)-10/1≥0`
`(60*R_2)/(60+R_2)-10/1≥0`
`(60*R_2-600-10R_2)/(60+R_2)≥0`
`(50*R_2-600)/(60+R_2)≥0`
Найдем нули
Знаменатель обращается в 0 при `R_2=-60`
Числитель:
`50*R_2-600=0`
`R_2=12`
Строим интервал, удовлетворяющий условиям
+ - +![]()
-60 12
Берем натуральное число, так как омы не могут быть отрицательными.
Ответ: 12
Номер: 2B06C4
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна `I=ε/(R+r)`, где 𝜀 — ЭДС источника (в вольтах), 𝑟=1 Ом — его внутреннее сопротивление, 𝑅 — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания `I_(кз)=ε/r` ? Ответ дайте в омах.
Решение:
`I≤0,2*I_(кз)`
`ε_1/(R+r)≤0,2*ε_1/r` | :ε1
`1/(R+1)≤1/5*1/1`
`1/(R+1)-1/5≤0`
`(5-R-1)/(5(R+1))≤0`
`(4-R)/(5(R+1))≤0`
Найдем нули, приравняв числитель и знаменатель к нулю
`5(R+1)=0`
`R =-1`
`4-R=0`
`R = 4`
- + -![]()
-1 4
Берем натуральное число, так как омы не могут быть отрицательными
Ответ: 4
Номер: mathege
Опорные башмаки шагающего экскаватора, имеющего массу 𝑚=1500 тонн представляют собой две пустотелые балки длиной 𝑙=15 метров и шириной 𝑠 метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой `p=(mg)/(2ls)`, где 𝑚 — масса экскаватора (в тоннах), 𝑙 — длина балок в метрах, 𝑠 — ширина балок в метрах, 𝑔 — ускорение свободного падения (считайте 𝑔=10 м/с2). Определите наименьшую возможную ширину опорных балок, если известно, что давление 𝑝 не должно превышать 200 кПа. Ответ дайте в метрах.
Решение:
`P≤200`
`(mg)/(2ls)≤200`
`(1500*10)/(2*15*S)≤200`
`5/S-2/1≤0`
`(5-2S)/S≤0`
Найдем нули, приравняв числитель и знаменатель к нулю
`5-2S=0`
`S = 5/2=2,5`
- + -![]()
0 2,5
Берем натуральное число. Минусовые значения нас не интересуют. 0 выколотая точка.
Ответ: 2,5
Номер: mathege
Автомобиль, масса которого равна 𝑚=2000 кг, начинает двигаться с ускорением, которое в течение 𝑡 секунд остаётся неизменным, и проходит за это время путь 𝑆=600 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно `F=(2mS)/t^2`. Определите наибольшее время после начала движения автомобиля, за которое он пройдeт указанный путь, если известно, что сила 𝐹, приложенная к автомобилю, не меньше 1500 Н. Ответ выразите в секундах.
Решение:
`F≥1500`
`(2mS)/t^2≥1500`
`(2*2000*600)/t^2-1500/1≥0`
`(2400000-1500t^2)/t^2≥0`
Найдем нули
`2400000-1500t^2=0`
`t^2=24000/15=1600`
`t=±40`
- + -![]()
0 40
Берем натуральное число, так как секунды могут быть только натуральным числом. Минусовые значения нас не интересуют, 0 выколотая точка.
Ответ: 40
Номер: mathege
Для поддержания навеса планируется использовать цилиндрическую колонну. Давление 𝑃 (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле `P=(4mg)/(πD^2)`, где 𝑚=1200 кг — общая масса навеса и колонны, 𝐷 — диаметр колонны (в метрах). Считая ускорение свободного падения 𝑔=10 м/с2, а 𝜋=3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ дайте в метрах.
Решение:
`P≤400000`
`(4mg)/(пD^2)≤400000`
`(mg)/(пD^2)≤100000`
`(1200*10)/(3D^2)-100000/1≤0`
`(400*10)/(D^2)-100000/1≤0`
`4/D^2-100/1≤0`
`(4-100D^2)/D^2≤0`
Найдем нули
`4-100D^2≤0`
`4=100D^2`
`D^2=4/100`
`D=±1/5`
Ну и из знаменателя получаем выколотую точку D=0
- + -![]()
0 0,2
Берем натуральное число
Ответ: 0,2
Номер: mathege
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна `P=m(v^2/L−g)`, где 𝑚 — масса воды в килограммах, 𝜈 — скорость движения ведёрка в м/с, 𝐿 — длина верёвки в метрах, 𝑔 — ускорение свободного падения (считайте 𝑔=10 м/с2). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 62,5 см? Ответ дайте в м/с.
Решение:
`P≥0`
`m*(V^2/L-g)≥0`
62,5 см = 0,625 м
`V^2/(0,625)-10/1≥0`
`(V^2-6,25)/(0,625)≥0` |*0,625
`V^2-6,25≥0`
`(V-2,5)(V+2,5)≥0`
V=±2,5
+ - +
-2,5 2,5
Берем натуральное число, отрицательные числа нас не интересуют.
Ответ: 2,5
Номер: mathege
Перед отправкой тепловоз издал гудок с частотой f0=192 Гц . Чуть позже гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f (в Гц) больше первого: она зависит от скорости тепловоза v (в м/с) по закону `f(v)=f_0/(1−v/c)` (Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 8 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c=300 м/с. Ответ дайте в м/с .
Решение:
`f(v)=f_0/(1−v/c)`
Задача сводится к решению неравенства `f(v)-f_0≥8`. Выпишем все параметры с учетом их размерностей:
f0=192 Гц
c=300 м/с
f(v) = 8 Гц
Далее, для определения минимальной скорости запишем выражение с выписанными значениями, приравняв левую и правую части неравенства, а также используя условие f(v)-f0=8:
`8=192/(1-v/300)-192`
`200=192/(1-v/300)`
`1-v/300=192/200`
`v=(200-192)/200 * 300`
`v=8/200 * 300`
`v = 12`
Ответ: 12
Решение методом интервалов:
`f≥f_0+8`
`f≥192+8`
`f≥200`
`f_0/(1-v/c)≥200`
`192/(1-v/300)≥200`
`192/(1-v/300)-200/1≥0`
`(192-200+2/3v)/(1/1-v/300)≥0`
`(2/3v-8):(300-v)/300≥0`
`((2/3v-8)*300)/(300-v)≥0` |:300
`(2/3v-8)/(300-v)≥0`
Найдем нули
`2/3v-8=0`
`v=12`
`300-v=0`
`v=300` выколота
- + -![]()
12 300
Ответ: 12
Номер: 344B7E (старый 5190)
При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону `l=l_0sqrt(1−v^2/c^2)`, где 𝑙0=75 м — длина покоящейся ракеты, 𝑐=3∙105 км/с — скорость света, а 𝜈 — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы её наблюдаемая длина стала не более 21 м? Ответ дайте в км/с.
Решение:
`l≤21`
`l_0sqrt(1-v^2/c^2)≤21`
`75sqrt(1-v^2/c^2)≤21`
`sqrt(1-v^2/c^2)≤21/75`
`sqrt(1-v^2/c^2)≤7/25`
`1-v^2/c^2≤7^2/25^2`
`1/1-49/625≤V^2/c^2`
`576/625≤V^2/c^2`
`576/625-V^2/c^2≤0`
`(576*c^2-625*V^2)/(625c^2)≤0` |`*625c^2`
`576*c^2-625*V^2≤0`
`(24c-25V)(24c+25V)≤0`
Найдем нули
`24c=25V`
`V = 24/25c`
`24c=-25V`
`V = -24/25c` выколота
- + -![]()
-24/25c 24/25c
Берем натуральное число, отрицательные значения не берем.
`24/25*300000=288000`
Ответ: 288000
Номер: mathege
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле `A(ω)=(A_0ω_p^2)/(|ω_p^2−ω^2|)`, где 𝜔 — частота вынуждающей силы (в с−1), 𝐴0 — постоянный параметр, ωp=300 с−1 — резонансная частота. Найдите максимальную частоту 𝜔, меньшую резонансной, для которой амплитуда колебаний превосходит величину 𝐴0 не более чем на 80%. Ответ дайте в с−1.
Решение:
`A≤A_0+0,8*A_0`
`A≤1,8A_0`
`(A_0*ω_p^2)/(|ω_p^2-ω^2|) ≤1,8A_0` |`:A_0` (оно положительно, знак не изменится)
`(ω_p^2)/(|ω_p^2-ω^2|) ≤1,8`
ω меньше ωp, значит разность в знаменателе положительна, можно раскрыть модуль, не меняя знаки
`(300^2)/(300^2-ω^2) -9/5 ≤0`
`(5*300^2-9*300^2+9ω^2)/(5*(300^2-ω^2))≤0`
`(9ω^2-4*300^2)/(5*(300^2-ω^2))≤0` |`*5*(300^2-ω^2)`
`(3ω-2*300)(3ω+2*300)≤0`
`(3ω-600)(3ω+600)≤0`
`ω=±600/2=±200`
+ - +
-200 200
Берем натуральное число, отрицательные значения не берем.
Ответ: 200
Номер: mathege
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле `A(ω)=(A_0ω_p^2)/(|ω_p^2−ω^2|)`, где 𝜔 — частота вынуждающей силы (в с−1), 𝐴0 — постоянный параметр, 𝜔𝑝=360 с−1 — резонансная частота. Найдите максимальную частоту 𝜔, меньшую резонансной, для которой амплитуда колебаний превосходит величину 𝐴0 не более чем на одну пятнадцатую. Ответ дайте в с−1.
Решение:
`A≤1*A_0+1/15*A_0`
`A≤16/15*A_0`
`(A_0*360^2)/(|360^2-ω^2|)≤16/15*A_0` |`:A_0`
ω меньше ωp, значит разность в знаменателе положительна, можно раскрыть модуль, не меняя знаки
`(360^2)/(360^2-ω^2)≤16/15`
`(360^2)/(360^2-ω^2)-16/15≤0`
`(15*360^2-16*360^2+16ω^2)/(15*(360^2-ω^2))≤0` |`*15(360^2-ω^2)`
`16ω^2-360^2≤0`
`(4ω-360)(4ω+360)≤0`
`ω=±360/4=±90`
+ - +
-90 90
Берем натуральное число, отрицательные значения не берем.
Ответ: 90
Номер: mathege
Иррациональные
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a (в км /ч2 ). Скорость v (в км/ч) вычисляется по формуле `v=sqrt(2la)`, где l — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 км, приобрести скорость 110 км/ч. Ответ дайте в км /ч2.
Решение:
`110=sqrt(2*1,1*a)`
`110^2=2*1,1*a`
`a=(110*110)/(2*1,1)=5500`
Ответ: 5500
Номер: 55D7D9
Наблюдатель находится на высоте h (в км). Расстояние l (в км) от наблюдателя до наблюдаемой им линии горизонта вычисляется по формуле `l=sqrt(2Rh)`, где R=6400 км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 96 км? Ответ дайте в км.
Решение:
`96=sqrt(2*6400*h)`
`96*96=2*6400*h`
`h=(96*96)/(2*6400)=(36*2)/(50*2)=72/100=0,72`
Ответ: 0,72
Номер: 8E8558
Наблюдатель находится на высоте h, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле `l=sqrt(Rh/500)`, где R=6400 км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 64 километра? Ответ дайте в метрах.
Решение:
`64=sqrt((6400*h)/500)`
`64^2=64/5*h`
`h=(64^2*5)/64=320` м
Ответ: 320
Номер: 69C186
Расстояние от наблюдателя, находящегося на высоте ℎ м над землёй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле `l=sqrt(Rh/500)`, где 𝑅=6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 5,6 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 10,4 километров?
Решение:
1) h при l=5,6
`5,6=sqrt((6400*h)/500)`
`5,6^2=64/5*h`
`h=(5,6*5,6*5)/64=(5,6*28)/64=(56*7)/(16*10)=49/20=2,45` м
2) h при l=10,4
`10,4=sqrt(64/5*h)`
`h=(10,4*10,4*5)/64=(10,4*52)/64=169/20=8,45` м
`8,45-2,45=6` м
Ответ: 6
Номер: mathege
Расстояние от наблюдателя, находящегося на высоте ℎ м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле `l=sqrt(Rh/500)`, где 𝑅=6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 километров. К пляжу ведёт лестница, каждая ступенька которой имеет высоту 10 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
Решение:
1) h при l=4,8
`4,8=sqrt((6400*h)/500)`
`4,8^2=64/5*h`
`h=(4,8*4,8*5)/64=(4,8*3)/64=(0,6*3)/8=1,8` м
2) h при l=6,4
`6,4=sqrt(64/5*h)`
`6,4^2=64/5*h`
`h=(6,4*6,4*5)/64=(6,4*32)/64=3,2` м
3) `3,2-1,8=1,4` м = 140 см
4) `140/10=14` ступенек
Ответ: 14
Номер: ЕГЭ 2017
Показательные
В ходе распада радиоактивного изотопа его масса уменьшается по закону `m=m_0⋅2^(−t/T)`, где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 96 мг. Период его полураспада составляет 3 мин. Найдите, через сколько минут масса изотопа будет равна 3 мг.
Решение:
`t= 3` мин
`m=96` мг
`m_0=3` мг
По формуле:
`3 = 96*2^(-t/3)`
`2^(-t/3)=3/96=1/32`
`2^(-t/3)=2^(-5)`
`-t/3=-5`
`t=5*3=15` мин
Ответ: 15
Номер: 76777E
При адиабатическом процессе для идеального газа выполняется закон pVk =6,4⋅106 Па⋅м5, где p — давление в газе в паскалях, V — объём газа (в м3), `k=5/3` . Найдите, какой объём V (в м3) будет занимать газ при давлении p, равном 2* 105 Па.
Решение:
`2*10^5*V^(5/3)=6,4*10^6` |`:10^5`
`2*V^(5/3)=64`
`V^(5/3)=32`
`V^(5/3)=2^5` |^1/5
`V^(1/3)=2^1` |^3
`V=2^3`
`V=8`
Ответ: 8
Номер: D888F6 (старый 5039)
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением `p_1V_1^(1,4)=p_2V_2^(1,4)`, где p1 и p2 — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Решение:
`V_1=294,4`л
`P_1=1` атм
`P_2=128` атм
`V_2-?`л
`1*294,4^(1,4)=128*V_2^(1,4)`
`V_2^(1,4)=(294,4^(1,4))/128`
`V_2^(1,4)=(294,4^(1,4))/2^7` |^5
`V_2^7=(294,4^7)/2^35` |^1/7
`V_2^1=(294,4^7)/2^5=(294,4*10)/(32*10)=2944/320=9,2`
Ответ: 9,2
Номер: F56EEF
Уравнение процесса, в котором участвовал газ, записывается в виде 𝑝𝑉𝑎=𝑐𝑜𝑛𝑠𝑡, где 𝑝 (Па) — давление в газе, 𝑉 — объём газа в кубических метрах, 𝑎 — положительная константа. При каком наименьшем значении константы 𝑎 увеличение вчетверо объёма газа, участвующего в этом процессе, приводит к уменьшению давления не менее, чем в 2 раза?
Решение:
`V_2=4*V_1`
`P_2≤P_1/2`
1)
`P_1*V_1^a=const`
`P_1=(const)/V_1^a`
`P_2*V_2^a=const`
`P_2=(const)/V_2^a`
2)
`(const)/V_2^a=(const)/(V_1^a*2)` | :const
`1/(4V_1)^a≤1/(V_1^a*2)` | `*V_1^a` *2
`2/(4^a)≤1`
`2^1/2^(2a)≤2^0`
`2^(1-2a)≤2^0`
`1-2a≤0`
`-2a≤-1`
`a≥1/2`
Ответ: 0,5
Номер: mathege
Уравнение процесса, в котором участвовал газ, записывается в виде 𝑝𝑉𝑎=𝑐𝑜𝑛𝑠𝑡, где 𝑝 (Па) — давление в газе, 𝑉 — объём газа в кубических метрах, 𝑎 — положительная константа. При каком наименьшем значении константы 𝑎 уменьшение вчетверо объёма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 8 раз?
Решение:
`V_2=1/4*V_1`
`P_2≥8*P_1`
1)
`P_1*V_1^a=const`
`P_1=(const)/V_1^a`
`P_2*V_2^a=const`
`P_2=(const)/V_2^a=(const)/(1/4*V_1)^a=(const*4a)/(V_1)^a`
2)
`(const*4^a)/(V_1)^a≥(8*const)/(V_1)^a` |`*V_1^a`
`4^a≥8`
`2^(2a)≥2^3`
`2a≥3`
`a≥1,5`
Ответ: 1,5
Номер: mathege
Логарифмы
Водолазный колокол, содержащий υ=2 моля воздуха при давлении p1 =1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением `A=αυTlog_2 p_2/p_1`, где α=13,3 Дж/моль⋅K — постоянная, T=300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
Решение:
`15960=13,3*2*300*log_2 P_2/(1,75)`
`log_2 P_2/(1,75)=15960/(133*2*30)=2`
`2^2=P_2/(1,75)`
`P_2=4*1,75=7`
Ответ: 7
Номер: AF6375
Для обогрева помещения, температура в котором поддерживается на уровне Tп=25 °C, через радиатор пропускают горячую воду. Расход проходящей через трубу радиатора воды m=0,3 кг /с. Проходя по трубе расстояние x, вода охлаждается от начальной температуры Tв=57 °C до температуры T, причём `x=α ⋅ (cm)/γ ⋅ log_2 (Tв−Tп)/(T−Tп)`, где с=4200 Вт⋅с/кг⋅°C — теплоёмкость воды, γ=63 Вт/м⋅°C — коэффициент теплообмена, α=1,4 — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 56 м.
Решение:
`56=1,4*(4200*0,3)/63*log_2 (57-25)/(T-25)`
`56=28*log_2 32/(T-25)`
`log_2 32/(T-25)=2`
`2^2=32/(T-25)`
`T-25=8`
`T=33`
Ответ: 33
Номер: 5CC0F4
Ёмкость высоковольтного конденсатора в телевизоре `C=6⋅10^(−6)` Ф. Параллельно с конденсатором подключён резистор с сопротивлением `R=8⋅10^6` Ом. Во время работы телевизора напряжение на конденсаторе U0=34 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением `t=αRClog_2 U_0/U` (с), где α=0,8 — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 76,8 секунды. Ответ дайте в кВ (киловольтах).
Решение:
`t≥76,8`
`α*R*c*log_2 (U_0/U)≥76,8` |:(α*R*c)
`log_2 34/U≥(76,8)/(0,8*8*10^6*6*10^(-6))`
`log_2 34/U≥(76,8)/(38,4)`
`log_2 34/U≥2`
`log_2 34/U≥log_2 4`
`34/U≥4/1`
`34/U-4/1≥0`
`(34-4U)/U≥0`
Найдем нули, приравняв числитель и знаменатель к нулю
- + -![]()
0 8,5
Берем положительное значение.
Ответ: 8,5
Номер: E01E0A
Тригонометрия
Двигаясь со скоростью 𝜈=3 м/с, трактор тащит сани с силой 𝐹=40 кН, направленной под острым углом 𝛼 к горизонту. Мощность, развиваемая трактором, вычисляется по формуле `N=Fvcosα`. Найдите, при каком угле α (в градусах) эта мощность будет равна 60 кВт (кВт — это `(кН*м)/с`).
Решение:
`60=40*3*cosα`
`cosα=60/120=1/2`
`α=60°`
если посмотреть по тригонометрическому кругу, то это будет 60 градусов, так как -60° не подходит, ведь физически направление силы между трактором и санями не может быть направлено вниз (под землю).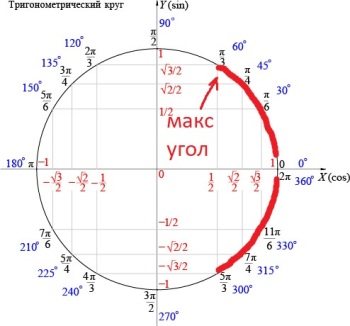
Ответ: 60
Номер: mathege
Трактор тащит сани с силой 𝐹=80 кН, направленной под острым углом 𝛼 к горизонту. Работа трактора (в килоджоулях) на участке длиной 𝑆=50 м вычисляется по формуле A=FScosα. При каком максимальном угле 𝛼 (в градусах) совершeнная работа будет не менее 2000 кДж?
Решение:
`A≥2000`
`F*S*cos∝≥2000`
`80*50*cos∝≥2000`
`cos∝≥1/2`
`∝_(max)=60°`
если посмотреть по тригонометрическому кругу, то это будет 60 градусов, так как -60° не подходит, ведь физически направление силы между трактором и санями не может быть направлено вниз (под землю).
Ответ: 60
Номер: ЕГЭ 2016
Мяч бросили под углом 𝛼 к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле `t=(2v0sinα)/g`. При каком наименьшем значении угла 𝛼 (в градусах) время полёта будет не меньше 2,1 секунды, если мяч бросают с начальной скоростью 𝑣0=21 м/с? Считайте, что ускорение свободного падения 𝑔=10 м/с2.
Решение:
`t≥2,1`
`(2*V_0*sin∝)/g≥2,1`
`(2*21*sin∝)/10≥2,1`
`4,2*sin∝≥2,1`
`sin∝≥1/2`
Соблюдение условия будет при
150°≥α≥30°
а наименьший угол 30°
`∝_(min)=30°`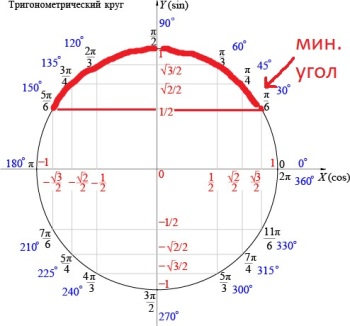
Ответ: 30
Номер: 562145
Плоский замкнутый контур площадью 𝑆=4 м2 находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой `ε_i=aScosα`, где 𝛼 — острый угол между направлением магнитного поля и перпендикуляром к контуру, 𝑎=3∙10−4 Тл/с — постоянная, 𝑆 — площадь замкнутого контура, находящегося в магнитном поле (в м2). При каком минимальном угле 𝛼 (в градусах) ЭДС индукции не будет превышать 6∙10−4 В?
Решение:
`ε_i≤6*10^(-4)`
`a*S*cosα≤6*10^(-4)`
`3*10^-4*4*cosα≤6*10^(-4)`
`cosα≤1/2`
`α_(min)=60º`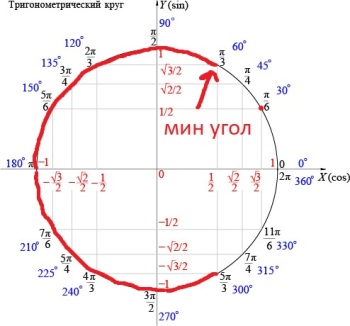
Ответ: 60
Номер: mathege
Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью 𝜈=4 м/с под острым углом 𝛼 к рельсам. От толчка платформа начинает ехать со скоростью `u=m/(m+M)` vcosα (м/с), где 𝑚=75 кг — масса скейтбордиста со скейтом, а 𝑀=300 кг — масса платформы. Под каким максимальным углом 𝛼 (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,4 м/с?
Решение:
`U≥0,4`
`m/(m+M)*V*cosα≥0,4`
`75/375*4*cosα≥0,4`
`1/5*4*cosα≥0,4` |*5
`4*cosα≥2` |:4
`cosα≥1/2`
`α_(max)=60º`
Ответ: 60
Номер: mathege
Катер должен пересечь реку, ширина которой 𝐿=90 м, а скорость течения 𝑢=1,5 м/с, так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением `t=L/u ctgα`, где 𝛼 — острый угол, задающий направление движения катера (отсчитывается от берега). Под каким минимальным углом 𝛼 (в градусах) нужно плыть, чтобы время в пути было не больше 60 с?
Решение:
`t≤60`
`L/U*ctgα≤60°`
`90/(1,5)*ctgα≤60°`
`60°*ctgα≤60°` |:60
`ctgα≤1`
`45°≤α≤90°`
значит минимальный угол будет 45°
Ответ: 45
Номер: ЕГЭ 2014
Два тела, массой m=2 кг каждое, движутся с одинаковой скоростью v=8 м /c под углом 2α друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле `Q=mv^2 sin^2 α`, где m — масса (в кг), v — скорость (в м/с). Найдите, под каким углом 2α должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 32 Дж. Ответ дайте в градусах.
Решение:
Составим уравнение исходя из условия
`32=2*8^2*sinα^2`
`sinα^2=32/128=1/4`
`sinα=±1/2`
α = 30°
В итоге если α=30 градусам, то 2α = 60°
Ответ: 60
Номер: D33D49
Деталью некоторого прибора является квадратная рамка с намотанным на неё проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Н ∙ м) определяется формулой `M=NIBl^2sinα`, где 𝐼=3 А — сила тока в рамке, 𝐵=4∙10−3 Тл — значение индукции магнитного поля, 𝑙=0,5 м — размер рамки, 𝑁=600 — число витков провода в рамке, 𝛼 — острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла 𝛼 (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент 𝑀 был не меньше 0,9 Н ∙ м?
Решение:
`M≥0,9`
`N*I*B*l^2*sinα≥0,9`
`600*3*4*10^-3*0,25*sinα≥0,9`
`1,8*sinα≥0,9`
`sinα≥1/2`
Соблюдение условия будет при
150°≥α≥30°
а наименьший угол 30°
Ответ: 30
Номер: mathege
Очень лёгкий заряженный металлический шарик зарядом 𝑞=5∙10−6 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет 𝜈=6 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции 𝐵 которого лежит в той же плоскости и составляет угол 𝛼 с направлением движения шарика. Значение индукции поля 𝐵=6∙10−3 Тл. При этом на шарик действует сила Лоренца, равная `F_л=qvBsinα` (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла 𝛼∈[0°;180°] шарик оторвётся от поверхности, если для этого нужно, чтобы сила 𝐹л была не менее, чем 9∙10−8 Н? Ответ дайте в градусах.
Решение:
`F_л≥9*10^(-8)`
`q*V*B*sinα≥9*10^(-8)`
`5*10^-6*6*6*10^-3*sinα≥9*10^(-8)`
`sinα≥(9*10^(-8))/(5*6*6*10^(-9))=10/(5*2*2)`
`sinα≥1/2`
Соблюдение условия будет при
150°≥α≥30°
а наименьший угол 30°
Ответ: 30
Номер: mathege
Небольшой мячик бросают под острым углом 𝛼 к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле `L=(v_0^2)/g sin2α` (м), где 𝜈0=13 м/с — начальная скорость мяча, а 𝑔 — ускорение свободного падения (считайте 𝑔=10 м/с2). При каком наименьшем значении угла (в градусах) мяч перелетит реку шириной 8,45 м?
Решение:
`L≥8,45`
`(V_0)^2/g*sin2α≥8,45`
`16,9*sin2α≥8,45`
`sin2α≥0,5`
`2α=30`°
Соблюдение условия для 2α=30° будет при
150°≥2α≥30°
а наименьший угол 2α=30°, то есть
`2α=30°`
`α=30/2=15°`
Ответ: 15
Номер: ЕГЭ 2015
При нормальном падении света с длиной волны 𝜆=450 нм на дифракционную решётку с периодом 𝑑 нм наблюдают серию дифракционных максимумов. При этом угол 𝜑 (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума 𝑘 связаны соотношением `dsinφ=kλ`. Под каким минимальным углом 𝜑 (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1800 нм?
Решение:
k=2
d≤1800
`(k*λ)/(sinφ)≤1800`
`(2*450)/(sinφ)≤1800` |:900
`1/(sinφ)-2/1≤0`
`(1-2sinφ)/(sinφ)≤0`
Найдем нули
- + -![]()
0 1/2
Исключаем сразу sinφ = 0 (выколотые точки 0 и 180 градусов)
`1-2sinφ=0`
`sinφ = 1/2`,
то есть 150°≥α≥30° при этом минимальный угол будет 30°
и для отрицательного интервала sinφ нам тоже подходит диапазон (нижний полукруг), но там по тригонометрическому кругу углы гораздо больше 30°, поэтому все таки берем 30°.
Ответ: 30
Номер: ЕГЭ 2015
Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полёта мячика Н (в м) вычисляется по формуле
`H=(v_0^2)/4g (1−cosα)`, где v0 =26 м /c — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/c2 ). При каком наименьшем значении угла α мячик пролетит над стеной высотой 7,45 м на расстоянии 1 м? Ответ дайте в градусах.
Решение:
`8,45=26^2/(4*10)*(1-cosα)`
`1-cosα=(8,45)/(26*26)`
`1-cosα=(169*2)/(26*26)=1/2`
`cosα=1/2`
`α=60°`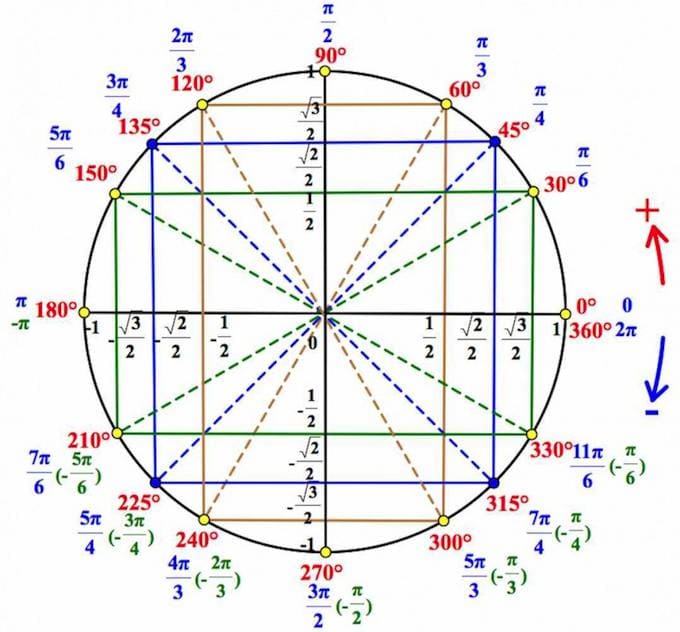
Ответ: 60
Номер: B3C046
Скорость колеблющегося на пружине груза меняется по закону `v(t)=7sin (πt)/4` (см/с), где 𝑡 — время в секундах. Какую долю времени из первых двух секунд скорость движения превышала 3,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Решение:
`V>3,5`
`7*sin (πt)/4>3,5` |:7
`sin (πt)/4>1/2`
`π/6+2πn<(π*t)/4<(5π)/6+2πn` |:π
`1/6+2n<t/4<5/6+2n` |*4
`2/3+8n<t<10/3+8n` ; n∈z

При n=0
`2/3<t<10/3`
__0___2/3___2___10/3___t
?
Нам необходимо найти долю времени до 2 секунд:
Получается `2-2/3=6/3-2/3=4/3` секунды была длительность времени от 2/3 с до 2 секунд.
Это доля от 2 секунд составляет `2/3` ее части, если 2 секунды рассматривать как целое. Ведь `4/3+2/3=6/3`, причем `4/3` больше `2/3` в два раза.
Тогда 2:3*2=0,6666≈0,67
Ответ: 0,67
Номер: mathege
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону `U=U_0sin(ωt+φ)`, где 𝑡 — время в секундах, амплитуда 𝑈0=2 В, частота 𝜔=240°/с, фаза 𝜑=−120°. Датчик настроен так, что если напряжение в нeм не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Решение:
`U≥1`
`U_0*sin(240t-120)≥1`
`2sin(240t-120)≥1` |:2
`sin(240t-120)≥1/2`
`30+360n≤240t-120≤150+360*n` |+120°
`150+360n≤240t≤270+360*n` |:240
`15/24+1,5n≤t≤27/24+1,5n`
При n = 0
`15/24≤t≤27/24`
__15/24___1или(24/24)___27/24______t
?
Нам необходимо найти долю времени до 1 секунды (до 24/24):
Получается `24/24-15/24=9/24` секунды была длительность времени горения до 1 секунды.
Если брать 1 секунду как `24/24` и 100%, то `9/24` будет часть от нее и х%.
`9/24-х%`
`24/24-100%`
`x = (9*100*24)/(24*24)=37,5%`
Ответ: 37,5
Номер: mathege
Разное
Независимое агентство намерено ввести рейтинг 𝑅 новостных изданий на основе показателей информативности 𝐼𝑛, оперативности 𝑂𝑝 и объективности 𝑇𝑟 публикаций. Каждый показатель оценивается целыми числами от 1 до 6.
Аналитик, составляющий формулу, считает, что объективность публикаций ценится вдвое, а информативность – вчетверо дороже, чем оперативность. В результате, формула примет вид `R=(4In+Op+2Tr)/A`.
Каким должно быть число 𝐴, чтобы издание, у которого все показатели наибольшие, получило рейтинг 1?
Решение:
`1=(4*6+6+2*6)/A`
`1=42/A`
`A =42`
Ответ: 42
Номер: 660E75
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности 𝐼𝑛, оперативности 𝑂𝑝, объективности 𝑇𝑟 публикаций, а также качества 𝑄 сайта. Каждый отдельный показатель — целое число от 0 до 4.
Составители рейтинга считают, что объективность ценится вчетверо, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид `R=(5In+Op+4Tr+Q)/A`
Если по всем четырём показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число 𝐴, при котором это условие будет выполняться.
Решение:
`R=(5R+R+4R+R)/A`
`R=(11*R)/A` |:R
`1=11/A`
`A=11`
Ответ: 11
Номер: mathege
Зависимость объёма спроса 𝑞 (единиц в месяц) на продукцию предприятия-монополиста от цены 𝑝 (тыс. руб.) задаётся формулой 𝑞=120−10𝑝. Выручка предприятия за месяц 𝑟 (тыс. руб.) вычисляется по формуле `r(p)=pq`. Определите наибольшую цену 𝑝, при которой месячная выручка 𝑟(𝑝) составит 320 тыс. руб. Ответ приведите в тыс. руб.
Решение:
`r(p)=320`
`pq=320`
`p(120-10p)-320=0`
`-10p^2+120p-320=0` |:(-10)
`p^2-12p+32=0`
`p_1=4`
`p_2=8`
Берем наибольшее значение по условию задания.
Ответ: 8
Номер: 5450F1
Зависимость объёма спроса 𝑞 (единиц в месяц) на продукцию предприятия-монополиста от цены 𝑝 (тыс. руб.) задаётся формулой 𝑞=190−10𝑝. Выручка предприятия за месяц 𝑟 (в тыс. руб.) вычисляется по формуле `r(p)=q⋅p`. Определите наибольшую цену 𝑝, при которой месячная выручка 𝑟(𝑝) составит не менее 700 тыс. руб. Ответ приведите в тыс. руб.
Решение:
`r(p)≥700`
`pq≥700`
`(190-10p)*p-700≥0`
`-10p^2+190p-700≥0` |:(-10)
`p^2-19p+70≤0`
`p_1=14`
`p_2=5`
+ - +
5 14
Берем наибольшее значение, согласно условию, это 14
Ответ: 14
Номер: F5E019
Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой
`η=(T_1−T_2)/T_1*100%`, где 𝑇1 — температура нагревателя (в кельвинах), 𝑇2 — температура холодильника (в кельвинах). При какой температуре нагревателя 𝑇1 КПД этого двигателя будет 25%, если температура холодильника 𝑇2=276 К? Ответ дайте в градусах Кельвина.
Решение:
`25=(T_1-276)/T_1*100`
`(T_1-276)/T_1=25/100=1/4`
`4(T_1-276)=T_1`
`4T_1-1104=T_1`
`3T_1=1104`
`T_1=368`
Ответ: 368
Номер: ЕГЭ 2019
Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой 𝑚в (в килограммах) от температуры 𝑡1 до температуры 𝑡2 (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы 𝑚др кг. Он определяется формулой `η=(c_вm_в(t_2−t1))/(q_(др)m_(др))*100%`, где 𝑐в=4,2∙103 Дж/(кг∙К) — теплоёмкость воды, 𝑞др=8,3∙106 Дж/кг — удельная теплота сгорания дров. Определите массу дров, которые понадобится сжечь в кормозапарнике, чтобы нагреть 𝑚=80 кг воды от 17°С до кипения, если известно, что КПД кормозапарника равен 14%. Ответ дайте в килограммах.
Решение:
`t_2=100`°C
`14/1=(4,2*10^3*80(100-17))/(8,3*10^6*m_(дров))*100`
`14m_(дров)=42*8`
`m_(дров)=(42*8)/14=3*8=24` кг
Ответ: 24
Номер: mathege
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: `F_A=apgr^3`, где 𝛼=4,2 — постоянная, 𝑟 — радиус аппарата в метрах, 𝜌=1000 кг/м3 — плотность воды, а 𝑔 — ускорение свободного падения (считайте 𝑔=10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 42000 Н? Ответ дайте в метрах.
Решение:
`F_a≤42000`
`α*ρ*g*r^3≤42000`
`4,2*1000*10r^3≤42000` |:1000
`42r^3≤42`
`r^3≤1`
`r^3≤1^3`
`r≤1` м
Ответ: 1
Номер: mathege
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: `F_A=pgl^3`, где 𝑙 — длина ребра куба в метрах, 𝜌=1000 кг/м3 — плотность воды, а 𝑔 — ускорение свободного падения (считайте 𝑔=9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ дайте в метрах.
Решение:
`F_a≤78400`
`ρ*g*l^3≤78400`
`1000*9,8*l^3≤78400` |:100
`98*l^3≤784`
`l^3≤8`
`l≤2`
Ответ: 2
Номер: mathege
Груз массой 0,16 кг колеблется на пружине. Его скорость v (в м/с) меняется по закону `v=v_0cos (2π t)/T`, где t — время с момента начала наблюдения в секундах, T=2 с — период колебаний, v0=1,5 м /с. Кинетическая энергия E (в Дж) груза вычисляется по формуле `E=mv^2/2`, где m — масса груза (в кг), v — скорость груза (в м/с). Найдите кинетическую энергию груза через 20 секунд после начала наблюдения. Ответ дайте в джоулях.
Решение:
1) `V=1,5*cos (2π*20c)/2=1,5*cos20π=1,5*1=1,5`
2) `E=(0,16*1,5^2)/2=16/100*3/2*3/2=18/100=0,18`
Ответ: 0,18
Номер: 9DD340
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время 𝑡 падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле `h=5t^2`, где ℎ — расстояние в метрах, 𝑡 — время падения в секундах. До дождя время падения камешков составляло 1,2 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,1 с? Ответ выразите в метрах.
Решение:
1) h до дождя = `5*1,2^2=5*6/5*1,2=7,20`м
2) t после дождя = `1,2-0,1=1,1` c
3) h после дождя =`5*1,1^2=5*1,21=6,05`м
`7,20-6,05=1,15` м
Ответ: 1,15
Номер: mathege
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f =20 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 15 до 40 см, а расстояние d2 от линзы до экрана — в пределах от 100 до 120 см. Изображение на экране будет чётким, если выполнено соотношение
`1/d_1+1/d_2=1/f`.
Укажите, на каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.
Решение:
При `d_2=100`
`1/d_1+1/100=1/20`
`1/d_1=1/20-1/100`
`1/d_1=4/100`
`d_1=100/4=25` см
При `d_2=120`
`1/d_1+1/120=1/20`
`1/d_1=1/20-1/120`
`1/d_1=5/100`
`d_1=120/5=24`см
берем наименьшее расстояние согласно условия.
Ответ: 24
Номер: 6FDB97
При температуре 0°С рельс имеет длину 𝑙0=12,5 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону `l(t°)=l_0(1+a*t°)`, где 𝛼=1,2∙10−5(°С )−1 — коэффициент теплового расширения, 𝑡° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.
Решение:
1) `l=l_0+6мм=12,5 м+6мм=12,5 м+0,006мм=12,506 м`
2) `12,506=12,5(1+1,2*10^-5*t)`
`12,506=12,5+12,5*1,2*10^-5*t`
`0,006=12,5*1,2*10^-5*t`
`t=(0,006*10^5)/(12,5*1,2*1)=(6*100)/(12,5*1,2)=40`
Ответ: 40
Номер: mathege
Для определения эффективной температуры звёзд используют закон Стефана– Больцмана, согласно которому мощность излучения P (в ваттах) нагретого тела прямо пропорциональна площади его поверхности и четвёртой степени температуры: `P=σST^4`, где `σ=5,7⋅10^(−8)` — постоянная, площадь поверхности S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь поверхности `S=1/18⋅10^(21)` м 2, а излучаемая ею мощность P равна `4,104⋅10^27` Вт. Определите температуру этой звезды. Дайте ответ в градусах Кельвина.
Решение:
`T^4=P/(σS)`
`T^4=(4,104*10^27)/(5,7*10^-8*1/18*10^21)`
`T^4=(4,104*10^14*18)/(5,7)=(4,104*10^12*100*18)/(5,7)=(410,4*10^12*18)/(5,7)` |*10/10
`T^4=(4104*10^12*18)/57`
`T^4=6^4*10^12`
`T=6*10^3`
`T=6000`
Ответ: 6000
Номер: C24CBD
Рейтинг 𝑅 интернет-магазина вычисляется по формуле `R=r_(пок)−(r_(пок)−r_(экс))/((K+1)^m)`, где `m=(0,02K)/(r_(пок)+0,1)`, `r_(пок)`− средняя оценка магазина покупателями, `r_(экс)` − оценка магазина, данная экспертами, 𝐾− число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,51.
Решение:
1) `m=(0,02*24)/(0,86+0,10)=(0,48)/(0,96)=1/2`
2) `R=0,86-(0,86-0,51)/((24+1)^(1/2))=0,86-(0,35)/(sqrt25)=0,86-(0,35)/5=0,86-0,07=0,79`
Ответ: 0,79
Номер: 1B9D7A
Рейтинг 𝑅 интернет-магазина вычисляется по формуле `R=r_(пок)−(r_(пок)−r_(экс))/((K+1)*(0,02K)/(r_(пок)+0,1))`,
где 𝑟пок− средняя оценка магазина покупателями (от 0 до 1), 𝑟экс− оценка магазина экспертами (от 0 до 0,7) и 𝐾− число покупателей, оценивших магазин.
Найдите рейтинг интернет-магазина «Бета», если число покупателей, оставивших отзыв о магазине, равно 20, их средняя оценка равна 0,25, а оценка экспертов равна 0,61.
Решение:
`R=0,25-(0,25-0,61)/(21*(0,02*20)/(0,25+0,10))=0,25+(0,36)/(21*(0,4)/(0,35))=0,25+(0,36*0,35*10000)/(21*0,4*10000)=0,25+15/1000=0,25+0,015=0,265`
Ответ: 0,265
Номер: CE0344

