Все прототипы расчетных задач из первой части ЕГЭ по профильной математике с решениями и ответами.
Движение по прямой
Два велосипедиста одновременно отправились в 140-километровый пробег. Первый ехал со скоростью, на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение:
Пусть x - скорость первого велосипедиста, тогда
x - 4 - скорость второго велосипедиста
`t_(медл)-t_(быстр)=4`
`140/(x-4) - 140/x = 4`
`140x - 140(x-4)= 4x(x-4)`
`560= 4x^2-16x`
`4x^2-16x-560=0`
`x^2-4x-140=0`
`D=16-4*1*-140=576`
`x=(4+24)/(2*1)=28/2=14`
второй корень отрицательный, не подходит
Ответ: 14
Номер: BC64EB
Два велосипедиста одновременно отправились в 160-километровый пробег. Первый ехал со скоростью, на 6 км/ч большей, чем скорость второго, и прибыл к финишу на 6 часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Решение:
Пусть х - скорость 2-го велосипедиста, тогда
х+6 -скорость 1-го велосипедиста
`t_(медл)-t_(быстр)=6`
`160/х - 160/(х+6) = 6`
`(160х+160*6-160x)/(x^2+6x)=6` |:6
`x^2 + 6x - 160 = 0`
По теореме Виета
`x_1+x_2=-6`
`x_1*x_2=-160`
`x_1 = 10` км/час
`x_2 = -16` (не удовлетворяет условию)
Ответ: 10
Номер: BAF165
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 132 км. На следующий день он отправился обратно со скоростью на 1 км/ч больше прежней. По дороге он сделал остановку на 1 час. В результате он затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из А в B. Ответ дайте в км/ч.
Решение:
В одном направлении скорость V = x км/ч, во втором V = x+1 км/ч.
Время, затраченное в одну сторону, `t = 132/x`, во вторую сторону `t = 132/(x+1)`, пройденный путь в ту и другую сторону S = 132
Составим уравнение
`132/x-132/(x+1)=1`
`(132x+132-132x)/(x^2+x)=1/1`
`x^2+x=132`
`x^2+x-132=0`
`D=1^2-4*1*(-132)=23^2`
`x=(-1+23)/2=11`
отрицательный корень не находим, так как в нем нет смысла
Ответ: 11
Номер: DB0573
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 187 км. На следующий день он отправился обратно в А со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из B в А. Ответ дайте в км/ч.
Решение:
В обратном направлении скорость V = x км/ч, из А в В V = x-6 км/ч.
Время, затраченное в обратную сторону, `t = 187/x`, из А в В `t = 187/(x-6)`, пройденный путь в ту и другую сторону S = 187
Составим уравнение
`t_(медл)-t_(быстр)=6`
`187/(x-6)-187/x=6`
`(187x-187x+187*6)/(x^2-6x)=6` |:6
`x^2-6x=187`
`x^2-6x-187=0`
`D=(-6)^2-4*1*(-187)=28^2`
`x=(6+28)/2=17`
отрицательный корень не находим, так как в нем нет смысла
Ответ: 17
Номер: 936503
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Решение:
Для первого автомобиля:
`V=x`
`t=(2y)/x`
`S=2y`
Для второго автомобиля:
1 половина пути
`V=x-13`
`t=y/(x-13)`
`S=y`
2 половина пути
`V=78`
`t=y/78`
`S=y`
Составим уравнение
`t_1=t_(2-1)+t_(2-2)`
`(2y)/x=y/(x-13)+y/78` |:y
`2/x-1/(x-13)=1/78`
`(2x-26-x)/(x^2-13x)=1/78`
`x^2-13x=78x-26*78`
`x^2-91x+26*78=0`
`D=8281-4*26*78=169=13^2`
`x_1=(91+13)/2=52` км/ч
`x_1=(91-13)/2=39` км/ч
39 не подходит по условию, так как там указано что скорость больше 48 км/ч
Ответ: 52
Номер: ЕГЭ 2021 mathege
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 42 км/ч, а вторую половину пути — со скоростью, на 28 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Решение:
Для первого автомобиля:
`V=x`
`t=(2y)/x`
`S=2y`
Для второго автомобиля:
1 половина пути
`V=42`
`t=y/42`
`S=y`
2 половина пути
`V=x+28`
`t=y/(x+28)`
`S=y`
Составим уравнение
`t_1=t_(2-1)+t_(2-2)`
`(2y)/x=y/42+y/(x+28)` |:y
`2/x-1/42=1/(x+28)`
`(2x+56-x)/(x^2+28x)=1/42`
`x^2+28x=42x+56*42`
`x^2-14x-56*42=0`
`D=196+4*56*42=196+9408=9604=98^2`
`x=(14±98)/2`
`x=56` км/ч
отрицательный корень не находим, так как в нем нет смысла
Ответ: 56
Номер: mathege
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали мотоциклист и велосипедист. Известно, что за час мотоциклист проезжает на 50 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 5 часов позже мотоциклиста. Ответ дайте в км/ч.
Решение:
Для мото
`V=x+50` км/ч
`t=60/(x+50)`
`S=60`
Для велосипеда
`V=x` км/ч
`t=60/x`
`S=60`
Составим уравнение
`t_(медл)-t_(быстр)=5`
`60/x-60/(x+50)=5`
`(60x+60*50-60x)/(x^2+50x)=5` |:5
`x^2+50x=600`
`x^2+50x-600=0`
`D=2500+4*1*600=4900=70^2`
`x=(-50+70)/2=10` км/ч
отрицательный корень не находим, так как в нем нет смысла
Ответ: 10
Номер: D03826
Товарный поезд каждую минуту проезжает на 900 метров меньше, чем скорый, и на путь в 180 км тратит времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Решение:
Товарный:
`V=x`км/ч
`t=180/x`
`S=180`
Скорый:
`V=x+54`км/ч
`t=180/(x+54)`
`S=180`
`V_(скор)=x+(900*60)/1000=x+54` км/ч
Составим уравнение:
`t_(медл)-t_(быстр)=3`
`180/x-180/(x+54)=3`
`(180x+180*54-180x)/(x^2+54x)=3`
`x^2+54x=3240`
`x^2+54x-3240=0`
`D=2916+12960=15876=126^2`
`x=(-54+126)/2=36`км/ч
отрицательный корень не находим, так как в нем нет смысла
Ответ: 36
Номер: mathege
Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 25 км. Путь из A в B занял у туриста 6 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
Решение:
Подъем:
`V=x-1`км/ч
`t=5`
`S=5(x-1)`
Спуск:
`V=x`км/ч
`t=1`
`S=x*1`
Составим уравнение:
`S_(подъем)+S_(спуск)=25`
`5(x-1)+x*1=25`
`5x-5+x=25`
`6x=30`
`x=5` км/ч
Ответ: 5
Номер: 4483
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город B на 12 часов раньше, чем велосипедист приехал в город А, а встретились они через 2 часа 30 минут после выезда. Сколько часов затратил на путь из города B в город A велосипедист?
Решение:
Мото:
Полный путь
`V=y/(x-12)`
`t=x-12` часов
`S=y`
До встречи
`V=y/(x-12)`
`t=2,5` часа
`S=(2,5y)/(x-12)`
Вело:
Полный путь
`V=y/x`
`t=x` часов
`S=y`
До встречи
`V=y/x`
`t=2,5` часов
`S=(2,5y)/x`
Составим уравнение
`S_(м. до встр.)+ S_(в. до встр.)=S_(весь)`
`(2,5y)/(x-12)+(2,5y)/x=y` |:y
`(2,5x+2,5x-30)/(x^2-12x)=1`
`x^2-12x=5x-30`
`x^2-17x+30=0`
`D=(-17)^2-4*1*30=169=13^2`
`x_1=(17+13)/2=15` часов
отрицательный корень не находим, так как в нем нет смысла
Ответ: 15
Номер: 34F721
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 150 метрам?
Решение:
Разница в скорости 1,5 км/ч, то есть за 1 час разница в расстоянии будет 1,5 км или за 60 минут 1500 метров.
Составим пропорцию
60 мин - 1500 м
x мин - 150 м
`x=(60*150)/1500=6` мин
Ответ: 6
Номер: mathege
Из двух городов, расстояние между которыми равно 480 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?
Решение:
Скорость сближения
`V = 75+85=160` км/ч
Время на сближение
`t = S/v=480/160=3` часа
Ответ: 3
Номер: mathege
Из городов A и B, расстояние между которыми равно 440 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 4 часа на расстоянии 240 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Решение:
Авто из города А
`V=x`
`t=4`
`S=200`
Авто из города В
`V=60`
`t=4`
`S=240`
Путь, пройденный автомобилем А до встречи, `440-240=200` км
тогда скорость `V = 200/4=50` км/ч
Ответ: 50
Номер: mathege
Расстояние между городами A и B равно 630 км. Из города A в город B выехал первый автомобиль, а через три часа после этого навстречу ему из города B выехал со скоростью 70 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
Решение:
Авто из города А
`V=x`
`t=4+3=7` ч
`S=350`
Авто из города В
`V=70`
`t=280/70=4` ч
`S=280`
`V = 350/7=50` км/ч
Ответ: 50
Номер: 305DDD
Автомобиль выехал с постоянной скоростью 51 км/ч из города А в город В, расстояние между которыми равно 357 км. Одновременно с ним из города С в город В, расстояние между которыми равно 351 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 30 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.
Решение:
Авто:
`V=51`
`t=7`
`S=357`
Мото:
`V=x`
`t=13/2`
`S=351`
1) `t_(авт)=357/51=7`ч - время до встречи
2) `t_(мот)=7-0,5=6,5` ч - время до встречи
3) `V_(мот)=(351*2)/12=54` км/ч
Ответ: 54
Номер: mathege
Расстояние между городами A и B равно 440 км. Из города A в город B со скоростью 50 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 80 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Решение:
Первый авто до встречи
За 1 час:
`V=50`
`t=1`
`S=50*1`
За 3 часа:
`V=50`
`t=3` (узнали в п.4 задачи)
`S=50*3`
Второй авто до встречи
`V=80`
`t=3` (узнали в п.4 задачи)
`S=80*3`
1) Вначале узнаем, сколько прошел 1 авто за 1 час.
`50*1=50` км
2) Далее узнаем скорость сближения
`50+80=130` км/ч
3) Узнаем, сколько прошли 2 авто.
`440-50=390` км
4) Узнаем время, которое потребовалось машинам, чтобы пройти это расстояние
`390/130=3` часа
4) Причем 1 прошел `50*3=150` км за 3 часа и `50*1=50` за 1 час.
Итого `150+50=200` км он уехал от города А
Ответ: 200
Номер: mathege
Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 1,5 км от дома. Один идёт со скоростью 2,2 км/ч, а другой — со скоростью 4,4 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? Ответ дайте в километрах.
Решение:
1 человек до встречи
`V=2,2`
`t=x/(2,2)`
`S=x`
2 человек
В одну сторону до конца пути
`V=4,4`
`t=(1,5)/(4,4)`
`S=1,5`
Обратно до встречи
`V=4,4`
`t=(1,5-x)/(4,4)`
`S=1,5-x`
Итак, пока первый прошел лишь часть пути до встречи, второй уже дошел до опушки и возвращался назад. Составим уравнение:
`x/(2,2)=(1,5)/(4,4)+(1,5-x)/(4,4)`
`x/(2,2)=(3-x)/(4,4)` |*4,4
`2x=3-x`
`3x=3`
`x=1` км
Ответ: 1
Номер: ЕГЭ 2017, 2019
Расстояние между городами А и В равно 420 км. Из города A в город B выехал автомобиль, а через 1 час следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в B. Найдите расстояние от А до С. Ответ дайте в километрах.
Решение:
Мото:
Из А до города С
`V=80`
`t=x/80`
`S=x` км - расстояние от А до С
Возвращение обратно из С в А то же самое:
`V=80`
`t=x/80`
`S=x` км
Авто:
От А до города С
`V=((420-x)*80)/x`
`t=x/80+1`
`S=x` км
От С до В
`V=((420-x)*80)/x`
`t=x/80`
`S=420-x` км
t авто от А до С можно выразить двумя способами: `x/80+1` или как `t=S/v` ⇒ `x:((420-x)*80)/x=x^2/((420-x)*80)`
Составим уравнение
`x/80+1=x^2/((420-x)*80)`
`(x+80)/80=x^2/((420-x)*80)`
`x^2=420x-x^2+420*80-80x`
`2x^2-340x-420*80=0`
`x^2-170x-420*40=0`
`x^2-170x-16800=0`
`D=28900+67200=96100=310^2`
`x=(170+310)/2=240` км
Ответ: 240
Номер: 791A06
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 14 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа 42 минуты после этого догнал первого. Ответ дайте в км/ч.
Решение:
Необходимо составить систему уравнений, отношения 2 и 3 велосипедиста и 1 и 3
2 и 3 велосипедист
для 2
`V=14` км/ч
`t=y+1`
`S=14(y+1)` км
для 3
`V=x` км/ч
`t=y`
`S=x*y` км
1 и 3 велосипедист
для 1
`V=15` км/ч
`t=y+6,7`
`S=15(y+6,7)` км
для 3
`V=x` км/ч
`t=y+4,7`
`S=x*(y+4,7)` км
Составим систему уравнений
`{(14(y+1)=xy),(15(y+6,7)=x(y+4,7)):}`
`15(y+6,7)=(14(y+1))/y * (y+4,7)` (умножим на y обе части)
`15y(y+6,7)=(14y+14) * (y+4,7)`
`15y^2+100,5y=14y^2+65,8+14y+65,8`
`y^2+20,7*y-65,8=0` (умножим на 10 обе части)
`10y^2+207y-658=0`
`D=42849+40*658=69169=263^2`
`y=(-207+263)/20=2,8`
второй корень не ищем, он не имеет смысла
`x=(14(2,8+1))/(2,8)=19` км/ч
Ответ: 19
Номер: mathege
Движение по воде
Моторная лодка прошла против течения реки 187 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
Решение:
Против течения:
`V=x-3` км/ч
`t=187/(x-3)`
`S=187` км
По течению:
`V=x+3` км/ч
`t=187/(x+3)`
`S=187` км
Составим уравнение
`t_(медл)-t_(быстр)=6`
`187/(x-3)-187/(x+3)=6/1`
`(187*x+187*3-187*x+187*3)/(x^2-9)=6`
`(6*187)/(x^2-9)=6/1 |:6`
`x^2-9=187`
`x^2=196`
`x=14` км/ч
отрицательное значение нас не интересует
Ответ: 14
Номер: 5CD026
Моторная лодка прошла против течения реки 252 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 16 км/ч. Ответ дайте в км/ч.
Решение:
Против течения:
`V=16-x` км/ч
`t=252/(16-x)`
`S=252` км
По течению:
`V=16+x` км/ч
`t=252/(16+x)`
`S=252` км
Составим уравнение
`t_(медл)-t_(быстр)=4`
`252/(16-x)-252/(16+x)=4`
`(252*16+252x-252*16+252x)/(256-x^2)=4`
`(2*252*x)/(256-x^2)=4` |:4
`(126*x)/(256-x^2)=1/1`
`126x=256-x^2`
`x^2+126x-256=0`
`x_1=-128`
`x_2=2` км/ч
берем положительное значение
Ответ: 2
Номер: 2ED701
От пристани А к пристани B, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов после этого следом за ним со скоростью на 8 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение:
1 теплоход
`V=x` км/ч
`t=153/x`
`S=153` км
2 теплоход
`V=x+8` км/ч
`t=153/(x+8)`
`S=153` км
Составим уравнение
`t_(медл)-t_(быстр)=8`
`153/x-153/(x+8)=8`
`(153x+153*8-153x)/(x^2+8x)=8` |:8
`153/(x^2+8x)=1/1`
`x^2+8x=153`
`x^2+8x-153=0`
`D=64-4*1*(-153)=26^2`
`x_1=(-8-26)/2=-17`
`x_2=(-8+26)/2=9`км/ч
берем положительное значение
Ответ: 9
Номер: E5DDDD
От пристани A к пристани B, расстояние между которыми равно 176 км, отправился с постоянной скоростью первый теплоход, а через 5 часов после этого следом за ним, со скоростью на 5 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.
Решение:
1 теплоход
`V=x-5` км/ч
`t=176/(x-5)`
`S=176` км
2 теплоход
`V=x` км/ч
`t=176/x`
`S=176` км
Составим уравнение
`t_(медл)-t_(быстр)=5`
`176/(x-5)-176/x=5`
`(176x-176x+176*5)/(x^2-5x)=5/1` |:5
`x^2-5x=176`
`x^2-5x-176=0`
`D=25-4*1*-176=27^2`
`x_1=(5+27)/2=16` км/ч
`x_2=(5-27)/2=-11`
берем положительное значение
Ответ: 16
Номер: mathege
Пристани A и B расположены на озере, расстояние между ними равно 264 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась тем же путём обратно со скоростью на 2 км/ч больше прежней, сделав по пути остановку на 1 час. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Решение:
Туда
`V=x` км/ч
`t=264/x`
`S=264` км
Обратно
`V=x+2` км/ч
`t=264/(x+2)`
`S=264` км
Составим уравнение
`t_(медл)-t_(быстр)=1`
`264/x-264/(x+2)=1`
`(264x+264*2-264x)/(x^2+2x)=1/1`
`x^2+2x=528`
`x^2+2x-528=0`
`D=4-4*1*-528=2116=46^2`
`x=-2+46/(2*1)=22` км/ч
берем положительное значение, отрицательное можно не считать
Ответ: 22
Номер: 8B3972
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 4 часа, баржа отправилась назад и вернулась в пункт А в 22:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 8 км/ч.
Решение:
Туда
`V=8+x` км/ч
`t=30/(8+x)`
`S=30` км
Обратно
`V=8-x` км/ч
`t=30/(8-x)`
`S=30` км
Составим уравнение
`t_(туда)+t_(стоян)+t_(обрат)=12`
`30/(8+x)+4+30/(8-x)=12`
`30/(8+x)+30/(8-x)=8`
`(240+30x+240+30x)/(64-x^2)=8`
`(2*240)/(64-x^2)=8/1` |:8
`64-x^2=60`
`x^2=4`
`x=±2`
Отрицательное значение не берем
Ответ: 2
Номер: C169EB
Теплоход проходит по течению реки до пункта назначения 775 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 28 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 61 час. Ответ дайте в км/ч.
Решение:
По течению:
`V=28+x` км/ч
`t=775/(28+x)`
`S=775` км
Против течения:
`V=28-x` км/ч
`t=775/(28-x)`
`S=775` км
Составим уравнение
`t_(туда)+t_(стоян)+t_(обрат)=61`
`775/(28+x)+5+775/(28-x)=61`
`775/(28+x)+775/(28-x)=56`
`(775*28-775x+775*28+775x)/(784-x^2)=56`
`(2*775*28)/(784-x^2)=56/1` |:56
`784-x^2=775`
`784-x^2-775=0`
`x^2=9`
`x=±3`
Отрицательное значение не берем
Ответ: 3
Номер: 5059
Теплоход проходит по течению реки до пункта назначения 384 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 48 часов. Ответ дайте в км/ч.
Решение:
По течению:
`V=x+4` км/ч
`t=384/(x+4)`
`S=384` км
Против течения:
`V=x-4` км/ч
`t=384/(x-4)`
`S=384` км
Составим уравнение
`t_(туда)+t_(стоян)+t_(обрат)=48`
`384/(x+4)+8+384/(x-4)=48`
`384/(x+4)+384/(x-4)=40`
`(384*x-384*4+384*x+384*4)/(x^2-16)=40`
`(2*384*x)/(x^2-16)=40` |:8
`(96*x)/(x^2-16)=5/1`
`5(x^2-16)=96x`
`5x^2-96x-80=0`
`D=9216+1600=10816=104^2`
`x=(96+104)/10=20` км/ч
Отрицательный корень не нужен, можно не считать
Ответ: 20
Номер: 2F20C1
Теплоход, скорость которого в неподвижной воде равна 24 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 2 часа, а в исходный пункт теплоход возвращается через 34 часа после отправления из него. Сколько километров прошёл теплоход за весь рейс?
Решение:
По течению:
`V=24+3=27` км/ч
`t=x/(2*27)=x/54`
`S=x/2` км
Против течения:
`V=24-3=21` км/ч
`t=x/42`
`S=x/2` км
Составим уравнение
`t_(туда)+t_(стоян)+t_(обрат)=34`
`x/54+2+x/42=34`
`x/54+x/42=32`
`(96x)/(54*42)=32/1` |:32
`3x=54*42` |:3
`x=54*14`
`x=756` км
Ответ: 756 км
Номер: FE9990
Байдарка в 10 : 00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки равна 3 км/ч.
Решение:
По течению:
`V=x+3` км/ч
`t=15/(x+3)`
`S=15`км
Против течения:
`V=x-3` км/ч
`t=15/(x-3)`
`S=15`км
Составим уравнение
`t_(туда)+t_(стоян)+t_(обрат)=8`
`15/(x+3)+1 ч 20 мин +15/(x-3)=8 ч`
`15/(x+3) +15/(x-3)=6 ч 40 мин = 20/3 ч`
`(15x-45+15x+45)/(x^2-9)=20/3`
`(30x)/(x^2-9)=20/3` |:10
`2x^2-18=9x`
`2x^2-9x-18=0`
`D=81+144=225=15^2`
`x=(9+15)/4=6` км/ч
Отрицательное не считаем, оно не нужно
Ответ: 6
Номер: C08222
Расстояние между пристанями A и B равно 192 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Решение:
Пусть x - собственная скорость яхты (в неподвижной воде)
По течению:
`V=x+4` км/ч
`t=192/(x+4)`
`S=192` км
Против течения:
`V=x-4` км/ч
`t=192/(x-4)`
`S=192` км
`192/(x+4) + 192/(x-4)` - время яхты в пути
`92/4 = 23` часа - время в пути плота
`23-3=20` время яхты в пути
Составим уравнение:
`192/(x+4) + 192/(x-4)=20`
`192(x-4) + 192(x+4)=20(x+4)(x-4)`
`384x=20(x^2-16)`
`20x^2-384x-320=0` |:4
`5x^2-96x-80=0`
`D=9216-4*5*80=10816=104^2`
`x=(96+104)/2*5=20`
Второй корень отрицательный, не подходит.
Ответ: 20
Номер: 4BA055
Весной катер идёт против течения реки в `1 2/3` раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в `1 1/2` раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Решение:
Пусть x - скорость течения весной
(x-1) - скорость течения летом
V - собственная скорость
(V-x) - весной против течения
(V+x) - весной по течению
(V-(x-1)) - летом против течения
(V+(x-1)) - летом по течению
Составим систему уравнений
`{((V+x)/(V-x)=5/3), ((V+(x-1))/(V-(x-1))=3/2):}`
Выразим V
`3(V+x)=5(V-x)`
`3V+3x=5V-5x`
`8x=2V`
`V=4x`
подставляем в нижнее уравнение в системе
`(4x+x-1)/(4x-x+1)=3/2`
`10x-2=9x+3`
`x=5`
Ответ: 5
Номер: Демоверсия 2015-2020
Средняя скорость
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 66 км/ч, а вторую половину времени — со скоростью 82 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
1 половина
`V=66` км/ч
`t=x`
`S=66x` км
2 половина
`V=82` км/ч
`t=x`
`S=82-x` км
Получаем:
`V_(ср)=(66x+82x)/(2x)=(148x)/(2x)=74` км/ч
Ответ: 74
Номер: mathege
Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа – со скоростью 45 км/ч, а затем два часа – со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
1 час
`V=115`
`t=1`
`S=115`
следующие 3
`V=45`
`t=3`
`S=135`
затем еще 2 часа
`V=40`
`t=2`
`S=80`
`V=(115+135+80)/(1+3+2)=330/6=55` км/ч
Ответ: 55
Номер: 081941
Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 200 км – со скоростью 100 км/ч, а затем 160 км – со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
1 способ
Первые 120:
`V=60`
`t=2`
`S=120`
следующие 200:
`V=100`
`t=2`
`S=200`
еще 160 км:
`V=120`
`t=160/120=4/3`
`S=160`
`V_(ср)=(120+200+160)/(2/1+2/1+4/3)=480/(16/3)=(480*3)/16=90` км/ч
Ответ: 90
2 способ:
Берем каждый час за 1 часть и находим среднее для этих частей, тем самым определяя среднюю скорость.
`120/60 = 2` части
`200/100=2` часа (части)
`160/120=1 1/3`
`(60*2+100*2+1 1/3*120)/(5 1/3)=480/(5 1/3) = 1440/16`= 90 км/ч Для удобства подсчетов знаменатель и множитель умножили на 3, чтобы избавиться от неправильной дроби.
Ответ: 90
Номер: 5504F2
Первую треть трассы автомобиль ехал со скоростью 100 км/ч, вторую треть — со скоростью 75 км/ч, а последнюю — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
1 треть
`V=100`
`t=y/100`
`S=y`
2 треть
`V=75`
`t=y/75`
`S=y`
3 треть
`V=60`
`t=y/60`
`S=y`
Составим уравнение
`V_(ср)=(3y)/(y/100+y/75+y/60)=(3y)/((12y)/300)=(900y)/(12y)=75` км/ч
Ответ: 75
Номер: mathege
Путешественник переплыл море на яхте со средней скоростью 24 км/ч. Обратно он летел на спортивном самолете со скоростью 456 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Решение:
Яхта
`V=24`
`t=x/24`
`S=x`
Самолет
`V=456`
`t=x/456`
`S=x`
Составим уравнение
`V=(x+x)/(x/24+x/456)=(2x)/((20x)/456)=(2x*456)/(20x)=45,6` км/ч
Ответ: 45,6
Номер: mathege
Поезд
Поезд, двигаясь равномерно со скоростью 50 км/ч, проезжает мимо придорожного столба за 72 секунды. Найдите длину поезда в метрах.
Решение:
1) `50` км/ч=`(50*1000)/3600=500/36` м/с
2) V поезда относительно столба = `500/36` м/с
t мимо столба = 72 с
Пройденный путь за 72 секунды
`500/36*72=1000` метров
Ответ: 1000
Номер: mathege
Поезд, двигаясь равномерно со скоростью 70 км/ч, проезжает мимо лесополосы, длина которой равна 1000 метров, за 1 минуту 48 секунд. Найдите длину поезда в метрах.
Решение:
1 мин 48 сек = 108 секунд
1) `70` км/ч `=(70*1000)/3600=700/36` м/с
2) V мимом лесополосы = `700/36` м/с
t мимо лесополосы = 108 с
Пройденный путь за 108 секунд
`700/36*108=2100 м`
3) 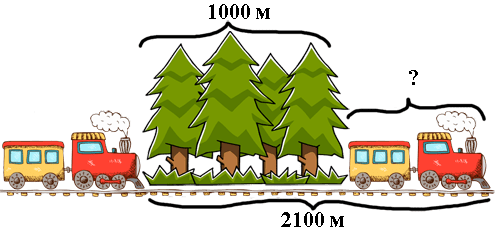
Надо учитывать, что если лесополоса 1000 м, а поезд проехал 2100 м, то разница как раз и будет длиной поезда.
Значит, между начальной и последней точкой поезда
2100-1000=1100 метров
Ответ: 1100
Номер: mathege
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 800 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 33 секундам. Ответ дайте в метрах.
Решение:
1) `V_(сближ)=70+50=120 ` км/ч
Это то же самое, что пассажирский стоит, а скорый движется мимо него со скоростью 120 км/ч.
2) `120 = (120*1000)/3600 = 100/3 м/c`
3) Найдем, сколько м прошел скорый поезд за 33 с
`S=100/3 * 33=1100` м
Итак, грузовой прошел 1100 метров мимо пассажирского поезда, причем, если бы он был физической точкой, то это было 800 метров, то есть лишние метры добавились благодаря его длине, где начальная и крайняя точка также были в определенное время напротив пассажирского
`1100-800=300` метров - длина скорого поезда
Ответ: 300
Номер: ЕГЭ 2013
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 2 минутам. Ответ дайте в метрах.
Решение:
1) `V_(сближ)=80-50=30` км/ч
Это то же самое, что товарняк стоит, а пассажирский проезжает мимо него со скоростью 30 км/ч.
2) `30 км/ч = (30*10000)/3600=100/12 м/с`
3) То есть при скорости в 30 км/ч если бы он был физической точкой он бы за 2 минуты прошел 800 метров, но на самом деле пройденный путь
`100/12*120=1000`м
То есть получается, лишние метры образовались из-за того, что пассажирский поезд тоже имеет свою длину. Тогда
4) 1000-800=200 м
Ответ: 200
Номер: ЕГЭ 2013
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 130 метров, второй — длиной 120 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 600 метров. Через 11 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 800 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение:
1) 
Получается второй сухогруз прошел 600 метров до первого, потом прошел вдоль него длину второго сухогруза, прошел еще свою длину и оторвался на 800 метров. Все это за 11 минут.
`S = 600+130+120+800=1650` метров
2) `t_(сближ)=11 мин=11/60 ч`
3) `1650` метров = `165/100` км
`V_(сближ)=165/100:11/60=165/100*60/11=9` км/ч
Ответ: 9
Номер: mathege
Сплавы и смеси
Смешали некоторое количество 19-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`0,19m+0,17m=x*2m` |:m
`0,19+0,17=2x`
`0,36=2x`
`x=0,18=18%`
Ответ: 18
Номер: 0DCA14
Смешали 3 литра 35-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`0,35*3+0,15*12=x*15`
`1,05+1,8=15*x`
`15x=2,85`
`x=285/(100*15)=0,19=19`%
Ответ: 19
Номер: mathege
В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`0,24*10+0*5=x*15`
`2,4=x*15`
`x=0,16=16%`
Ответ: 16
Номер: 5FDF16
Первый сплав содержит 5% меди, второй – 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`0,05*m_1+0,13*(m_1+9)=0,11*(m_1+m_1+9)`
`0,05*m_1+0,13*m_1+1,17=0,22*m_1+0,99`
`0,18=0,04*m_1`
`m_1=4,5`
`m_1+m_1+9=4,5+4,5+9=18`
Ответ: 18
Номер: 72E65F
Имеется два сплава. Первый сплав содержит 5% меди, второй – 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`0,05*m_1+0,14*(m_1+10)=0,12(m_1+m_1+10)`
`0,05*m_1+0,14*m_1+1,4=0,24m_1+1,2`
`0,2=0,05*m_1`
`m_1=4`
`m_1+m_1+10=4+4+10=18`
Ответ: 18
Номер: 671196
Имеется два сплава. Первый содержит 10% никеля, второй – 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`{(0.1m_1+0.35*m_2=0.25*150),(m_1+m_2=150):}`
Из нижнего
`m_1=150-m_2`
Из верхнего
`0,1*(150-m_2)+0,35*m_2=37,5`
`15-0,1*m_2+0,35*m_2=37,5`
`0,25*m_2=22,5` |*4
`m_2=90`
`m_1=150-90=60` кг
90-60=30 кг составляет разница масс
Ответ: 30
Номер: 5AA449
Имеется два сосуда. Первый содержит 60 кг, а второй – 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 45% кислоты. Сколько процентов кислоты содержится в первом сосуде?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`{(x*60+y*20=0.3*80),(xm+ym=0.45*2m):}`
Из нижнего
`x+y=0,9`
`y=0,9-x`
Из верхнего
`60x+20(0,9-x)=24`
`60x+18-20x=24`
`40x=6`
`x=6/40=(3*5)/(20*5)=0,15=15%`
Ответ: 15
Номер: B968FE
Имеется два сосуда. Первый содержит 80 кг, а второй – 70 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 63% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 65% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`{(x*80+y*70=0.63*150),(xm+ym=0.65*2m):}`
Из нижнего
`x+y=1,3`
`y=1,3-x`
Из верхнего
`80*x+70*(1,3-x)=94,5`
`80x+91-70x=94,5`
`10x=3,5` |:10
`x=0,35=35%`
`80x=80*0,35=28`
35% от 80 кг это `0,35*80=28` кг
Ответ: 28
Номер: 4462
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
Решение:
Доля1*m1+Доля2*m2=Доля3*(m1+m2)
`{(0.45*m_1+0.97*m_2+0*10=0.62*(m_1+m_2+10)),(0.45*m_1+0.97*m_2+0.5*10=0.72*(m_1+m_2+10)):}`
Второе минус первое:
`5=0,1*(m_1+m_2+10)` |*10
`50=m_1+m_2+10`
Выразим m2
`m_2=40-m_1`
Подставим m2 в m1
`0,45*m_1+0,97(40-m_1)=0,62*50`
`0,45*m_1+38,8-0,97*m_1=31`
`7,8=0,52*m_1`
`m_1=(7,8)/(0,52)=780/522=30/2=15` кг
Ответ: 15
Номер: 02C0F1
Задачи на проценты
Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов одиннадцать таких же рубашек дороже куртки?
Решение:
9 рубашек дешевле куртки на 10% означает, что 9 рубашек составляют 100-10=90% от стоимости куртки.
Следовательно, одна рубашка – это 90/9=10 % от стоимости куртки, а 11 рубашек 10*11=110 %
110 - 100 = 10 %
Ответ: 10
Краткое оформление:
Куртка - 100%
9 рубашек - 90 %
1 рубашка - 90:9=10%
11 рубашек 10*11=110%
110-100=10%
Ответ: 10
Номер: 2B0545
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение:
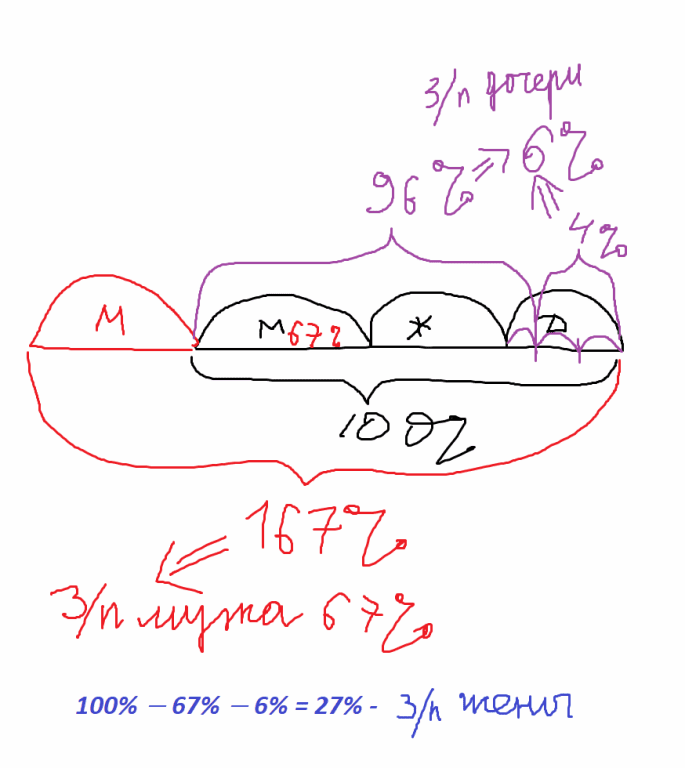
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%, то есть зарплата мужа составляет 67% дохода семьи.
Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%, то есть 2/3 стипендии составляют 4% дохода семьи, а вся стипендия дочери составляет 6% дохода семьи. Таким образом, доход жены составляет
100% − 67% − 6% = 27% дохода семьи.
Ответ: 27
ИЛИ
Пусть доход мужа, жены и дочери составляет x, y и z % соответственно. Тогда первое уравнение: x+y+z=100. Если зарплату мужа увеличить вдвое (зарплата станет 2х), то общий доход увеличиться на 67 %, то есть второе уравнение будет: 2x+y+z=167. Если стипендию дочери уменьшить втрое (стипендия станет z/3), то общий доход уменьшиться на 4 %, то есть третье уравнение будет иметь вид:
`x+y+z/3=96`.
Таким образом, получаем систему уравнений:
`{(x+y+z=100),(2x+y+z=167),(x+y+z/3=96):}`
Вычтем из второго уравнения первое: `2x—x+y—y+z—z=167—100` ⇔ `x=67`.
Вычтем из первого уравнения третье: `x—x+y—y+z—z/3=100—96` ⇔ `(2z)/3=4` ⇔ `z=6`.
Подставляя найденные x и z в первое уравнение, получим: `67+y+6=100` ⇔ `y=27`.
Ответ: 27
Номер: FD8828
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 42 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Решение:
| Изюм 19% воды 81 % сухого вещества |
Виноград 82% воды 18% сухого вещ. |
42кг - 100% x - 81% `x=(42*81)/100` (кг) сухого вещества |
`(42*81)/100` - 18 % x -100% `x=((42*81)/100)/18=189` кг |
Ответ: 189 кг
Номер: C7D297
Бизнесмен Печенов получил в 2000 году прибыль в размере 1000000 рублей. Каждый следующий год его прибыль увеличивалась на 16% по сравнению с предыдущим годом. Сколько рублей заработал Печенов за 2002 год?
Решение:
Увеличение на 16% это 116 % или 1,16
1 000 000*1,16*1,16=100*116*116=1 345 600 р.
Ответ: 1345600
Номер: mathege
В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 1%, а в 2010 году — на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
Решение:
увеличение за год% - это `(1+г/100)`
увеличение на 1% - это 1,01
увеличение на 9% - это 1,09
40000*1,01*1,09=4*101*109=404*109=40 400+3 636=44 036
Ответ: 44036
Номер: mathege
Митя, Артем, Паша и Женя учредили компанию с уставным капиталом 200000 рублей. Митя внес 18% уставного капитала, Артем — 60000 рублей, Паша — 0,18 уставного капитала, а оставшуюся часть капитала внес Женя. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1100000 рублей причитается Жене? Ответ дайте в рублях.
Решение:
1)
Миша - 18%
Артем - 60000 руб.
60000 - x%
200000 - 100%
Паша 0,18=18%
Женя 100-18-30-18=34%
2) 1100000 - 100%
x - 34%
`x=(1100000*34)/100=374 000` руб.
Ответ: 374000
Номер: mathege
Клиент А. сделал вклад в банке в размере 3800 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 418 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Решение:
| Вклад клиента А | Дата | Вклад клиента Б |
| 3800 |
янв 2018 |
|
| `3800(1+г/100)` | дек 2018 | |
| янв 2019 |
`3800` | |
| `3800(1+г/100)^2` | дек 2019 | `3800(1+г/100)` |
`3800(1+г/100)^2-3800(1+г/100)=418`
Пусть `(1+г/100)=t`
`3800t^2-3800t=418` |:38
`100t^2-100t=11`
`100t^2-100t-11=0`
`D=10000+4400=14400=120^2`
`t=(100+120)/100=220/200=1,1`
увеличение за год `1+г/100=1,1`⇒ 10%
Ответ: 10
Номер: mathege
Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 4000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2004 году, имея капитал в размере 4500 долларов, и, начиная с 2005 года, ежегодно получала прибыль, составляющую 200% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2007 года, если прибыль из оборота не изымалась?
Решение:
| Компания Альфа | год | Компания Альфа |
| `4000` | 2001 | |
| `4000+4000=4000*2^1` | 2002 | |
| `4000*2^2` | 2003 | |
| `4000*2^3` | 2004 | `4500` |
| `4000*2^4` | 2005 | `4500+2*4500=4500*3` |
| `4000*2^5` | 2006 | `4500*3^2` |
| `4000*2^6` Итого 256000 |
2007 | `4500*3^3` Итого 121500 |
`256000-121500=134500`
Ответ: 134500
Номер: mathege
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение:
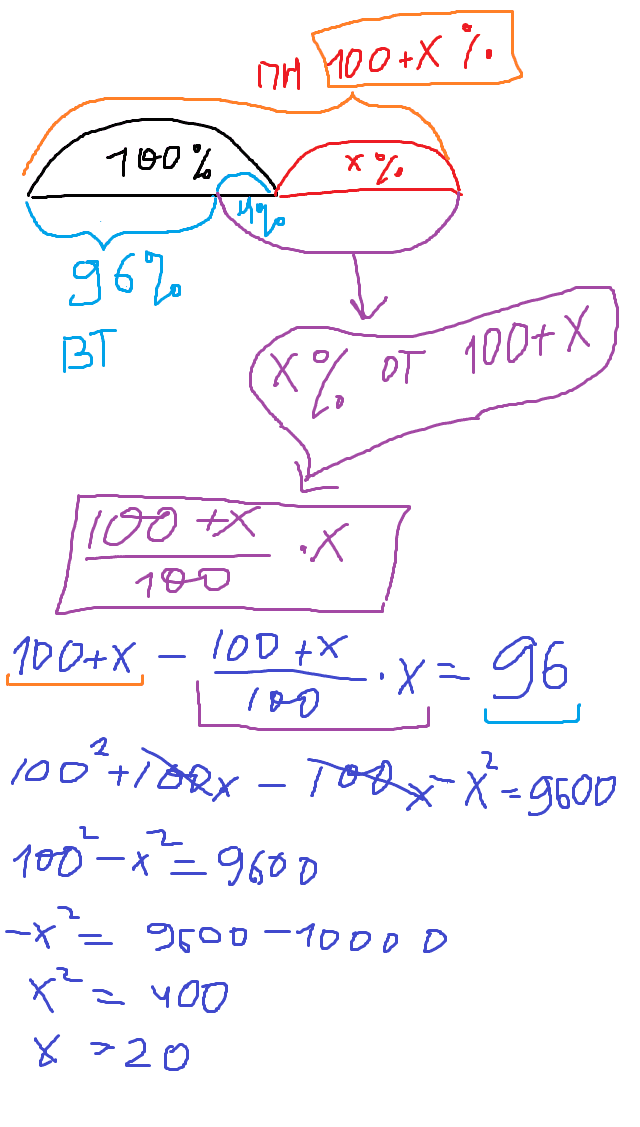
Ответ: 20
Ловите лайфхак. К данным в условии процентам дописываем два нуля и извлекаем корень. Это и будет ответ.
ИЛИ
Пусть S - начальная стоимость акций, х - десятичная запись процентов, на которые дважды происходили изменения стоимости акций. (Десятичная запись процентов - это представление процентов в виде десятичной дроби, например, десятичная запись 55% равна 0,55.)
В понедельник акции подорожали на х процентов, т.е. их стоимость увеличилась на S * х и составила
S+S*x=S(1+x).
Во вторник акции подешевели на х процентов, те. их стоимость уменьшилась на S(1 + х)*х.
Цена акций стала равна
S(1 + х) — S(1 + х) * х = S(1+х)(1 — х),
что составило 100% — 4% = 96% от цены в начале недели (от S). На основании этого составим уравнение:
S(1 + x)(1 - x) = 0,96S
(1 + x)(1 - x) = 0,96
1-x2 = 0,96
x2 = 0,04
Поскольку х > 0,то х = 0,2.
Следовательно, в понедельник и во вторник стоимость акций изменялась на 20%
Ответ: 20
ИЛИ
Обозначим первоначальную стоимость акций за А. Пусть в понедельник акции подорожали на х %, поэтому они стали стоить (100 + х)% от А, то есть
`A⋅(100+x)/100`.
Во вторник они подешевели на х %, поэтому они стали стоить (100 – х) % от `A⋅(100+x)/100`, то есть `A⋅(100+x)/100⋅(100—x)/100`.
В результате акции стали стоить 96% от А:
`A⋅96/100`.
Таким образом, получаем уравнение:
`A⋅(100+x)/100⋅(100—x)/100=A⋅96/100`|:A ⇔ `(100^2—x^2)/100=96` ⇔ `10000—x^2=9600` ⇔
⇔ `x^2=400` ⇔ `x_1=20`; `x_2=—20`.
Так как x>0, то акции подорожали в понедельник на 20%.
Ответ: 20
ИЛИ
Пусть х - десятичная запись количества процентов на которые дорожали и дешевели акции.
100% = 1 – первоначальная стоимость акций;
100 – 4 = 96% = 0,96 – конечная стоимость акций.
Составим уравнение по условию задачи:
1·(1 + х)·(1 – х) = 0,96
1 – х2 = 0,96
–х2 = 0,96 – 1
–х2 = –0,04
х2 = 0,04
х = ±√0,04
х = ±0,2
Количество процентов должно быть положительным, значит акции дорожали и дешевели на 0,2 = 20%.
Ответ: 20
Номер: 716AB2
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20900 рублей, через два года был продан за 16929 рублей.
Решение:
уменьшение на год г% - это (1-г/100)
`20900*(1-г/100)*(1-г/100)=16929`
`20900*(1-г/100)^2=16929`
`(1-г/100)^2=16929/20900=81/100`
1 корень
`1-г/100 = 9/10`
`г/100=1/10`
`г=10` %
или 2 корень
`1-г/100 = -9/10`
`г/100=19/10`
`г=190` %
190 не подходит, так как больше 100
Ответ: 10
Номер: mathege
Производительность
Заказ на 140 деталей первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 4 детали больше?
Решение:
| Произ. | Время | Кол. дет | |
| 1 | `x+4` | `140/(x+4)` | 140 |
| 2 | `x` | `140/x` | 140 |
Составим уравнение
`t_(медл)-t_(быстр)=4`
`140/x-140/(x+4)=4`
`(140x+140*4-140x)/(x^2+4x)=4/1` |:4
`x^2+4x=140`
`x^2+4x-140=0`
`D=16-4*1*(-140)=576=24^2`
`x_1=(-4+24)/2=10` дет.
отрицательный корень не ищем
Ответ: 10
Номер: D6FFD6
Заказ на 176 деталей первый рабочий выполняет на 5 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 5 деталей больше, чем второй?
Решение:
| Произ. | Время | Кол. дет | |
| 1 | `x` | `176/x` | 176 |
| 2 | `x-5` | `176/(x-5)` | 176 |
Составим уравнение
`t_(медл)-t_(быстр)=5`
`176/(x-5)-176/x=5`
`(176x-176x+176*5)/(x^2-5x)=5/1` |:5
`x^2-5x-176=0`
`D=25-4*1*(-176)=729=27^2`
`x_1=(5+27)/2=32/2=16`
отрицательный корень не ищем
Ответ: 16
Номер: 1C7F25
Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 112 литров она заполняет на 6 минут быстрее, чем первая труба?
Решение:
| Произ. | Время | Кол. л | |
| 1 | `x-6` | `112/(x-6)` | 112 |
| 2 | `x` | `112/x` | 112 |
`t_(медл)-t_(быстр)=6`
`112/(x-6)-112/x=6`
`(112x-112x+112*6)/(x^2-6x)=6/1` |:6
`x^2-6x-112=0`
`D =36-4*1*(-112)=484=22^2`
`x=(6+22)/2=14`
отрицательный корень не считаем
Ответ: 14
Второй способ:
Пусть I труба х л/мин, заполняет 112 литров за 112/х минут
II труба (х+6) л/мин, заполняет 112 литров за 112/(х+6) минут
Разница 112/х - 112/(х+6) = 6
Составим уравнение
`112/x - 112/(х+6) = 6`
`112(х+6) - 112х = 6х(х+6)`
`112*6 = 6х^2 + 6*6х`
`6х^2 + 6*6х - 112*6 = 0` Делим на 6
`х^2 + 6х - 112 = 0`
`D = 62 - 4*1*(-112) = 36 + 448 = 484 = 22^2`
`x_1 = (-6-22)/2 < 0` не удовлетворяет условию задачи, не может быть отрицательным значением
`x_2 = (-6+22)/2 = 16/2 = 8`
`8+6=14` литров в минуту пропускает вторая труба
Ответ: 14
Номер: 1E4FB8 (старый 5097)
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
Решение:
| Произв | Время | Кол литров | |
| 1 | `x` | `110/x` | 110 |
| 2 | `x+1` | `99/(x+1)` | 99 |
Составим уравнение
`t_(медл)-t_(быстр)=2`
`110/x-99/(x+1)=2`
`(110x+110-99x)/(x^2+x)=2/1`
`(11x+110)/(x^2+x)=2/1`
`2x^2+2x=11x+110`
`2x^2-9x-110=0`
`D=81+880=31^2`
`x=(9+31)/4=10` л
Ответ: 10
Номер: mathege
Первая труба пропускает на 8 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем вторая труба?
Решение:
| Произв | Время | Кол. л | |
| 1 | `x` | `180/x` | 180 |
| 2 | `x+8` | `180/(x+8)` | 180 |
`t_(медл)-t_(быстр)=8`
`180/x-180/(x+8)=8`
`(180x+180*8-180x)/(x^2+8x)=8/1` |:8
`x^2+8x=180`
`x^2+8x-180=0`
`D=64-4*1*(-180)=784=28^2`
`x=(-8+28)/2=10` л
отрицательный корень не ищем
Ответ: 10
Номер: BC2088
Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?
Решение:
| Произв | Время | Кол. л | |
| 1 | `x-5` | `500/(x-5)` | 500 |
| 2 | `x` | `375/x` | 375 |
`t_(медл)-t_(быстр)=10`
`500/(x-5)-375/x=10`
`(500x-375x+375*5)/(x^2-5x)=10/1`
`(125x+375*5)/(x^2-5x)=10/1` |:5
`(25x+375)/(x^2-5x)=2/1`
`2x^2-10x=25x+375`
`2x^2-35x-375=0`
`D=1225+3000=4225=65^2`
`x=(35+65)/4=25`
отрицательный корень не ищем
Ответ: 25
Номер: mathege
На изготовлении 60 деталей первый рабочий тратит на 4 часа меньше, чем второй рабочий на изготовление 80 таких же деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
Решение:
| Произв | Время | Кол. | |
| 1 | `x+2` | `60/(x+2)` | 60 |
| 2 | `x` | `80/x` | 80 |
`t_(медл)-t_(быстр)=4`
`80/x+60/(x+2)=4`
`(80x+160-60x)/(x^2+2)=4`
`(20x+160)/(x^2+2)=4/1` |:4
`(5x+40)/(x^2+2)=1`
`x^2+2x=5x+40`
`x^2-3x-40=0`
`D=9-4*1*40=169`
`x=(3+13)/2=8`
отрицательный корень не имеет смысла, его не считаем
Ответ: 8
Номер: 662145
На изготовление 540 деталей первый рабочий затрачивает на 12 часов меньше, чем второй рабочий на изготовление 600 деталей. Известно, что первый рабочий за час делает на 10 деталей больше, чем второй. Сколько деталей в час делает первый рабочий?
Решение:
| Произв | Время | Кол. | |
| 1 | `x` | `540/x` | 540 |
| 2 | `x-10` | `600/(x-10)` | 600 |
`t_(медл)-t_(быстр)=12`
`600/(x-10)-540/x=12`
`(600x-540x+5400)/(x^2-10x)=12/1`
`(60x+5400)/(x^2-10x)=12/1` |:12
`(5x+450)/(x^2-10x)=1/1`
`x^2-10x=5x+450`
`x^2-15x-450=0`
`D=225+1800=2025=45^2`
`x=(15±45)/2`
`x=60/2=30`
отрицательный корень не имеет смысла, его не ищем
Ответ: 30
Номер: 5A6244
Петя и Митя выполняют одинаковый тест. Петя отвечает за час на 10 вопросов теста, а Митя — на 16. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Мити на 117 минут. Сколько вопросов содержит тест?
Решение:
| Произв | Время | Кол. | |
| Петя | 10 в час | `x/10` | x |
| Митя | 16 в час | `x/16` | x |
`t_(медл)-t_(быстр)=117` мин или `39/20` ч
`x/10-x/16=39/20`
`(3x)/80=39/20` |перемножим крест накрест и :3
`20x=13*80` |:20
`x=13*4`
`x=52`
Ответ: 52
Номер: ЕГЭ 2017
Плиточник должен уложить 240 м2 плитки. Если он будет укладывать на 6 м2 в день больше, чем запланировал, то закончит работу на 9 дней раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Решение:
| Произв | Время | Кол. | |
| Петя | 10 в час | `x/10` | x |
| Митя | 16 в час | `x/16` | x |
`t_(медл)-t_(быстр)=9`
`240/x-240/(x+6)=9`
`(240x+240*6-240x)/(x^2+6)=9/1` |:9
`x^2+6x=160`
`x^2+6x-160=0`
`D=36-4*1*(-160)=676=26^2`
`x=(-6+26)/2=10`
отрицательный корень не ищем
Ответ: 10
Номер: mathege
Совместная работа
Один мастер может выполнить заказ за 30 часов, а другой – за 15 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Решение:
| Произв. | Время | Кол. з | |
| 1 | 1/30 заказа в час | 30 ч | 1 заказ |
| 2 | 1/15 заказа в час | 15 ч | 1 заказ |
| Вместе | ? =1/10 | x | 1 заказ |
1)`1/30+1/15=3/30=1/10`
2) `1:1/10=1*10/1=10` - t вместе
Ответ: 10
Номер: 9CCF41
Валя и Галя пропалывают грядку за 35 минут, а одна Галя — за 60 минут. За сколько минут пропалывает грядку одна Валя?
Решение:
| Произв. | Время | Кол. грядок | |
| Валя | 1/x грядки/минут | x | 1 |
| Галя | 1/60 грядки/минут | 60 | 1 |
| Вместе | 1/35 грядки/минут | 35 | 1 |
`1/x+1/60=1/35`
`1/x=1/35-1/60`
`1/x=5/420`
`x=(420*1)/5=84`
Ответ: 84
Номер: mathege
Первый насос наполняет бак за 1 час, второй — за 1 час 30 минут, а третий — за 1 час 48 минут. За сколько минут наполнят бак три насоса, работая одновременно?
Решение:
| Произв. | Время мин | Кол. баков | |
| 1 | 1/60 бака в мин | 60 | 1 |
| 2 | 1/90 бака в мин | 90 | 1 |
| 3 | 1/108 бака в мин | 108 | |
| Вместе | 1/27 бака в мин | x | 1 |
`1/60+1/90+1/108=20/540=1/27`
`t_(общ)=1/(1/27)=27`
Ответ: 27
Номер: mathege
Две трубы наполняют бассейн за 1 час 55 минут, а одна первая труба наполняет бассейн за 46 часов. За сколько часов наполняет бассейн одна вторая труба?
Решение:
| Произв. | Время | Кол.басс | |
| 1 | 1/46 бас в час | 46 | 1 |
| 2 | 1/60 бас в час | x | 1 |
| Вместе | 12/23 бас в час | 23/12 | 1 |
1) 1 час 55 мин = `1 + 55/60=23/12` ч
2) `1/46+1/x=12/23` |:46
`1+46/x=24`
`46/x=23`
`x=2`
Ответ: 2
Номер: mathege
Первая труба наполняет резервуар на 13 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 42 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Решение:
| Произв. | Время мин | Кол. рез | |
| 1 | `1/(x+13)` резервуар в минуту | x+13 | 1 |
| 2 | `1/x` резервуар в минуту | x | 1 |
| Вместе | `1/42` резервуар в минуту | 42 | 1 |
`1/(x+13)+1/x=1/42`
`(x+x+13)/(x^2+13x)=1/42`
`x^2+13x=81x+42*13`
`x^2-71x-546=0`
`D=5041+2184=7225=85^2`
`x=(71+85)/2=78`
отрицательный корень не имеет смысла
Ответ: 78
Номер: 4E4109
Первый садовый насос перекачивает 8 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 36 литров воды?
Решение:
| Произв. | Время мин | Кол. л | |
| 1 | 4 л в минуту | 2 | 8 |
| 2 | `8/7` л в минуту | 7 | 8 |
| Вместе | `36/x` л в минуту | x | 36 |
1) `8/2=4` л в минуту производительность 1 насоса
2) `8/8=8/7` л в минуту производительность 2 насоса
3) `4/1+8/7=36/x`
`36/7=36/x`
`x=7`
Ответ: 7
Номер: mathege
Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 16 часов. Через 2 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Решение:
| Произв. | Время | Кол. | |
| 1 | `1/16` зак в час | 16 час | 1 заказ |
| 1 | `1/16` | 2 часа | `2/16` заказа |
| Осталось `1-2/16=14/16` заказа | |||
| Вместе | `2/16` заказа в час | ? =7 |
`14/16` заказа |
`14/16:2/16=7` час работали вместе чтобы доделать заказ
7+2=9 часов получилось все время на выполнение заказа, так как 2 часа до совместных 7 часов работа л 1 рабочий.
Ответ: 9
Номер: mathege
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 4 дня выполняет такую же часть работы, какую второй — за 3 дня?
Решение:
| Произв. | Время | Кол. | |
| 1 | 1/x объем работы в день | x | 1 объем работы |
| 2 | 1/y объем работы в день | y | 1 объем работы |
| Вместе | 1/12 объем работы в день | 12 | 1 объем работы |
| 1 | 1/x объем работы в день | 4 | 4/x объем работы |
| 2 | 1/y объем работы в день | 3 | 3/y объем работы |
1) Приравняем работу первого и второго, выразим время для второго:
`4/x=3/y`
`y=(3x)/4`
2) Зная, что производительность за день равна 1/12 от все работы, так как они ее выполняют за 12 дней, составим уравнение
`1/x +1/y=1/12`
`1/x+(1*4)/(3x)=1/12`
`7/(3x)=1/12`
`3x=7*12` |:3
`x=28` дней
Ответ: 28
Номер: mathege
Игорь и Паша могут покрасить забор за 24 часа. Паша и Володя могут покрасить этот же забор за 30 часов, а Володя и Игорь — за 40 часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение:
| Произв | Время ч | Кол. заборов | |
| И и П | 1/24 забора в час | 24 | 1 |
| П и В | 1/30 забора в час | 30 | 1 |
| В и И | 1/40 забора в час | 40 | 1 |
| 2И+2П+2В | 1/24+1/30+1/40=2/20 | ||
| И+П+В | 1/20 забора в час | ? | 1 |
Узнаем их общую производительность помноженную на 2
`1/24+1/30+1/40=12/120=2/20`
То есть условно 1 производительность всех ребят это `2/20 : 2 = 1/20` забора за час
Значит время, ушедшее на покраску всего забора, будет равно:
`t=1/(1/20)=20` часов
Ответ: 20
Номер: mathege
Первый и второй насосы наполняют бассейн за 10 минут, второй и третий — за 14 минут, а первый и третий — за 15 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение:
| Произ басс в минуту | Время мин | Кол басс | |
| 1и2 | 1/10 | 10 | 1 |
| 2и3 | 1/14 | 14 | 1 |
| 1и3 | 1/15 | 15 | 1 |
| 2*1бас +2*2бас + 2*3бас | 1/10+1/14+1/15=50/210 | ||
| 1и2и3 | 25/210 | ? | 1 |
1) Узнаем их общую производительность, помноженную на 2
`1/10+1/14+1/15=50/210`
то есть общая производительность, умноженная на 1, будет
`50/210:2 = 25/210` бассейнов в минуту
Теперь найдем время для 1 бассейна
`t=1/(25/210)=210/25=42/5=8,4`мин
Ответ: 8,4
Номер: ЕГЭ 2016, 2017
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 18 рабочих, а во второй — 22 рабочих. Через 9 дней после начала работы в первую бригаду перешли 3 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Решение:
| 1 бригада | кол дней | 2бригада |
| 18 чел | 9 дней | 22 чел |
| 21 чел | y дней | 19 чел |
| Рабочих | Производ (заказ в день) |
Время | Кол |
| 1 | 1/x | x дней | 1 заказ |
| 18 | 18/x | ||
| 21 | 21/x | ||
| 22 | 22/x | ||
| 19 | 19/x | ||
| 18 | 18/x | 9 | 18/x*9 |
| 21 | 21/x | y | 21/x*y |
| 22 | 22/x | 9 | 22/x*9 |
| 19 | 19/x | y | 19/x*y |
* выделенная работа красным равна 1 заказу, выделенная синим работа тоже равна 1 заказу.
Составим систему уравнений
`{(18/x*9+21/x*y=1),(22/x*9+19/x*y=1):}`
`{((162+21y)/x=1),((198+19y)/x=1):}`
`{(x=162+21y),(x=198+19y):}`
`162+21y=198+19y`
`2y=36`
`y=18`
получается из первой таблицы, что первая бригада работала 9 дней, а потом с людьми, которые перешли из 2 бригады, еще 18 дней. Итого:
9+18=27 дней
Ответ: 27
Номер: mathege
Движение по окружности
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 22 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости другого?
Решение:
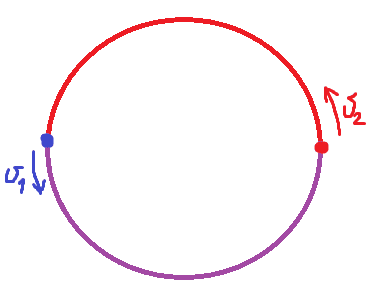
Получается, они расположены диаметрально противоположно (в разных концах диаметра), при этом надо одному мотоциклисту догнать другого, а это состоится при условии, что он отстает на `22/2=11` км.
Скорость сближения равна 20 км/ч.
Тогда время равно расстояние деленное на скорость
`t = 11/20=33/60=33` мин
Ответ: 33
Номер: mathege
Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
1 способ
Если они стартовали одновременно, то через 20 минут получается первый автомобиль обгонял второй на периметр круга, на 12 км.
То есть можно узнать "скорость удаления". Она равна периметр круга разделить на время, лучше сразу в часах, чтобы получились км/ч.
`20 мин =1/3` часа.
`V = 12/(1/3)=36 ` км/ч то есть на столько скорость первого авто выше второго.
Тогда 101-36=65 км/ч скорость 2 авто.
Ответ: 65
2 способ
Если они стартовали одновременно, то через 20 минут первый автомобиль обгонял второй на периметр круга, на 12 км.
То есть можно узнать "скорость удаления". Она равна периметр круга разделить на время, лучше сразу в часах, чтобы получились км/ч.
`20 мин =1/3` часа.
Для 1 авто (быстрое):
V=101
t=1/3
S=101/3
Для 2 авто (медлен.):
V=x
t=1/3
S=x/3
При этом за эту треть часа разница в расстоянии получилась равна 12 км.
Тогда выразим путь пройденный для 1 и 2 авто и приравняем к их разнице в 12 км.
Sбыстр. - Sмедл. = 12
`101/3-x/3=12` |*3
`101-x=36`
`x=65` км/ч - это скорость 2 авто
Ответ: 65
Номер: mathege
Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 44 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 33 км. Ответ дайте в км/ч.
Решение:
Встреча мотоцикла и велосипеда произошла через `30+10 = 40` минут после выезда велосипеда и через 10 минут после выезда мотоцикла. Значит их скорости пропорциональный времени, за которое они прошли одно и тоже расстояние.
`40/10=4` - во столько раз скорость вело ниже скорости мото.
В итоге, если взять за х скорость велосипедиста, то скорость мото будет `4x`.
Скорость сближения будет `4x-x=3x`.
Кроме того, мы знаем, что через 44 минуты мотоциклист догнал велосипедиста второй раз. То есть получается, что круг в 33 км при скорости сближения 3x он преодолел за 44 минуты.
Причем 44 минуты это `44/60=11/15` часа
Если выразить скорость сближения в км/ч, получаем 33 км за `11/15` часа
`V = 33/(11/15)=3*15=45` км/ч получилась скорость сближения.
Теперь найдем скорость велосипедиста.
`3x=45`
`x=15` км/ч
а скорость мотоциклиста в 4 раза больше.
`15*4=60` км/ч
Ответ: 60
Номер: mathege
Два гонщика участвуют в гонках. Им предстоит проехать 99 кругов по кольцевой трассе протяжённостью 4 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 22 минуты. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 20 минут? Ответ дайте в км/ч.
Решение:
Примем за х скорость второго гонщика.
Тогда время за которое он проедет всю трассу будет равно расстояние трассы деленное на его скорость, то есть:
`t_1 = (99*4)/x`
Причем за 20 минут первый обгонял второго на 4 км, на 1 круг. Отсюда можно узнать скорость удаления.
20 минут это 1/3 часа.
То есть за 1/3 часа получился разрыв в 4 км, тогда за час будет:
4*3=12 км/ч - скорость сближения.
Получается скорость 2 гонщика равна x+12 км/ч
Тогда время за которое он проедет всю трассу будет равно расстояние трассы деленное на его скорость, то есть:
`t_2 = (99*4)/(x+12)`
При этом мы знаем, что время первого от второго различается на 22 минуты
`22` минуты = `22/60=11/30` часа.
Составим уравнение:
`t_(медл)-t_(быстр)=11/30`
`(99*4)/x - (99*4)/(x+12) = 11/30`
`(396x+396*12-396x)/(x^2+12x) = 11/30` |:11
`(36x+36*12-36x)/(x^2+12x) = 1/30`
`432/(x^2+12x) = 1/30`
`x^2+12x = 11/30`
`x^2+12x = 12960`
`x^2+12x - 12960 = 0`
`D = 144+51480=51984=228^2`
`x=(-12+228)/2=108` км/ч
отрицательный корень не имеет смысла
Ответ: 108
Номер: mathege
Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?
Решение:
Скорости стрелок различаются в 12 раз. Если у часовой скорость x, то у минутной 12x
Если выразить все в делениях, то получается, что 12 делений в час минутной равны 1 делению в час часовой.
Из этого можно найти скорость сближения стрелок.
V сближ = 12-1=11 делений в час.
1 раз до "касания" минутной стрелки часовой.
В итоге до первого сближения надо пройти 7 полных делений и 1 неполное.
1 неполное равно 3/4 полных, так как 45 минут равно 3/4 часа или 3/4 того само деления где сейчас находится часовая стрелка.
`7+3/4=31/4` деления
При сближении 11 делений в час получаем время:
`S/V=(31/4)/11=31/44` часа
последующие 6 раз до "касания" минутной стрелки часовой.
Здесь минутной стрелке каждый раз придется проходить по 12 делений, то есть круг.
Тогда время на круг будет
`S/V=12/11` часа
Составим итоговое выражение для 1 сближения и последующих 6
`31/44+6*12/11=31/44+72/11=319/44` часа
Нам надо в минутах, тогда
`319/44*60=435` минут
Ответ: 435
Номер: mathege
Прогрессии
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 11 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 33 метрам.
Решение:
Арифметическая прогрессия
`S_n=(a_1+a_n)/2*n`
`a_1+a_n=11`
n-?
Sn=33
`33=11/2*n` |*2
`66=11*n`
`n=6`
Ответ: 6
Номер: mathege
Рабочие прокладывают тоннель длиной 99 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 7 метров туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 9 дней.
Решение:
Арифметическая прогрессия
`S_n=(a_1+a_n)/2*n`
`S_n=99`
`a_1=7`
`a_n=?`
`n=9`
`99/1=(7+a_n)/2*9` |:9
`22=7+a_n`
`a_n=15`
Ответ: 15
Номер: mathege
Бригада маляров красит забор длиной 810 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 180 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Решение:
Арифметическая прогрессия
`S_n=(a_1+a_n)/2*n`
`S_n=810`
`a_1+a_n=180`
`810=180/2*n`
`810=90*n`
`n=9`
Ответ: 9
Номер: mathege
Пете надо решить 333 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Петя решил 5 задач. Определите, сколько задач решил Петя в последний день, если со всеми задачами он справился за 9 дней.
Решение:
Арифметическая прогрессия
`S_n=(a_1+a_n)/2*n`
`S_n=333`
`a_1=5`
`a_n=?`
`n=9`
`333/1=(5+a_n)/2*9` |:9
`74=5+a_n`
`a_n=69`
Ответ: 69
Номер: mathege
Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 8 километров. Определите, сколько километров прошел турист за четвертый день, если весь путь он прошел за 10 дней, а расстояние между городами составляет 215 километров.
Решение:
Арифметическая прогрессия
`a_n=a_1+d(n-1)`
`S_n=(a_1+a_n)/2*n`
`a_1=8`
`n=10`
`S_n=215`
`a_4=?`
1) `215=(8+a_10)/2*10`
`215=(8+a_10)*5` |:5
`43=(8+a_10)`
`a_10=35`
2) `a_10=a_1+d*(10-1)`
`35=8+d*9`
`27=9d`
`d=3`
3) `a_4=a_1+d*(4-1)`
`a_4=8+3*3=17`
Ответ: 17
Номер: mathege
Лене надо подписать 972 открытки. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Лена подписала 20 открыток. Определите, сколько открыток было подписано за седьмой день, если вся работа была выполнена за 18 дней.
Решение:
Арифметическая прогрессия
`a_n=a_1+d(n-1)`
`S_n=(a_1+a_n)/2*n`
`S_n=972`
`a_1=20`
`a_7=?`
`n=18`
1) `972=(20+a_(18))/2*18` |:9
`108=(20+a_(18))`
`a_(18)=88`
2) `a_(18)=a_1+d*(18-1)`
`88=20+d*17`
`68=17d`
`d=4`
3) `a_7=a_1+d*(7-1)`
`a_7=20+4*6=44`
Ответ: 44
Номер: mathege
Грузовик перевозит партию щебня массой 360 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 3 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 18 дней.
Решение:
Арифметическая прогрессия
`a_n=a_1+d(n-1)`
`S_n=(a_1+a_n)/2*n`
`S_n=360`
`a_1=3`
`a_9=?`
`n=18`
1) `360=(3+a_(18))/2*18`
`360=(3+a_(18))*9` |:9
`40=3+a_(18)`
`a_(18)=37`
2) `a_(18)=a_(1)+d(18-1)`
`37=3+d*17`
`34=17d`
`d=2`
3) `a_9=a_1+d*(9-1)`
`a_9=3+2*8=19`
Ответ: 19
Номер: mathege

