§35. Ковалентная химическая связь. Часть II
Задание №1
Постройте график зависимости длины химической связи от ее кратности. При выполнении задания используйте различные источники информации.
Сделайте вывод.
Ответ:
Построим график, где l − это длина связи, k − кратность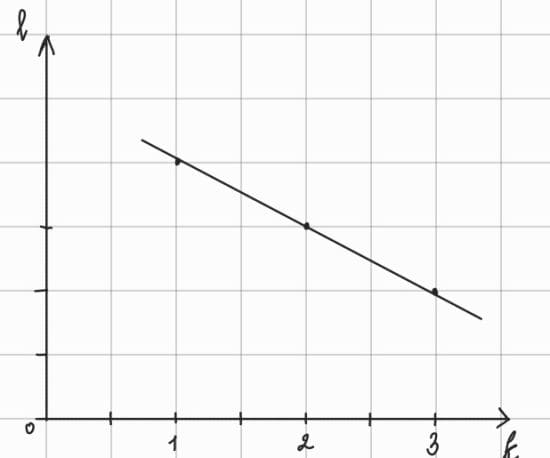
Вывод: чем выше кратность, тем меньше длина связи.
Задание №2
Постройте график зависимости прочности химической связи от ее кратности. При выполнении задания используйте различные источники информации.
Сделайте вывод.
Ответ:
Построим график, где p − это прочность связи, k − кратность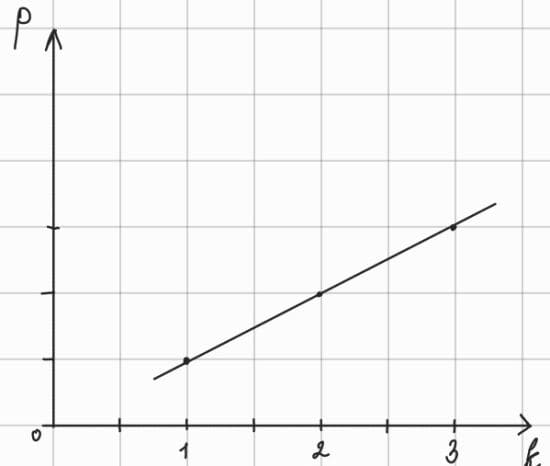
Вывод: чем выше кратность, тем прочнее связь.
Задание №3
Установите соответствие между структурной формулой и названием вещества.
СТРУКТУРНАЯ ФОРМУЛА ВЕЩЕСТВА
1) Э − Э
2) Э = Э
3) Э ≡ Э
↑↓
НАЗВАНИЕ ВЕЩЕСТВА
А) Бром
Б) Азот
В) Кислород
Ответ:
| 1 | 2 | 3 |
Ответ:
Ответ:
| 1 | 2 | 3 |
| А | В | В |
Задание №4
Какой объём (н.у.) займут 56 г азота? Какое число атомов и молекул содержит такое количество азота? Сколько ковалентных связей участвует в образовании молекул этого количества азота?
Ответ:
Дано:
m $(N_{2})$ = 56 г
Найти:
V ($N_{2}$) − ?
N (атомов) − ?
N (молекул) − ?
N (связей) − ?
Решение:
V ($N_{2}$) = n * Vm
n ($N_{2}$) = m : M = 56 г : 28 г/моль = 2 моль
V ($N_{2}$) = 2 моль * 22,4 л/моль = 44,8 л
N (атомов) = n * Na = 2 моль * 6 * $10^{23}$ = 12 * $10^{23}$ атомов
N (молекул) = 2 * n * Na = 2 * 2 моль * 6 * $10^{23}$ = 24 * $10^{23}$ молекул
В одной молекуле азота три связи, значит:
N (связей) = N (молекул) * 3 = 24 * $10^{23}$ молекул * 3 = 36 * $10^{23}$ связей
Ответ: V ($N_{2}$) = 44,8 л; N (атомов) = 12 * $10^{23}$ атомов; N (молекул) = 24 * $10^{23}$ молекул; N (связей) = 36 * $10^{23}$ связей
Задание №5
Выберите вещества с ковалентной неполярной химической связью: $NH_{3}, H_{2}O, Br_{2}, Cl_{2}, CO_{2}, O_{3}, NaCl, P_{4}, K_{2}SO_{4}, HCl$
Ответ:
Вещества с ковалентной неполярной химической связью: $Br_{2}, Cl_{2}, O_{3}, P_{4}$

