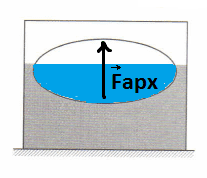
Задание 51.1. Тело частично погружено в жидкость.
а) Закрасьте часть тела, погруженную в жидкость. Запишите формулу для вычисления выталкивающей (архимедовой) силы, действующей на это тело, используя нужные из приведенных ниже физических величин:
$F_{A}$ − архимедова сила;
$ρ_{т}$ − плотность материала тела;
$ρ_{ж}$ − плотность жидкости;
$V_{ж}$ − объём жидкости;
$V_{т}$ − объём всего тела;
$V_{тж}$ − объём части тела, погружённой в жидкость;
g − коэффициент пропорциональности в формуле.

$F_{А} = gρ_{ж}V_{тж}$.

б) Изобразите на рисунке архимедову силу.

Задание 51.2. Два кубика одинакового размера, но изготовленные из разных материалов, погружены в жидкость.
а) Закрасьте части кубиков, погружённые в жидкость.

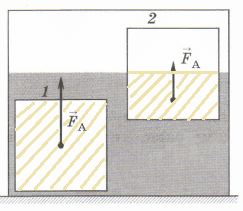
б) Как отличаются объёмы закрашенных частей кубиков

$V_{тж1} = 2V_{тж2}$

в) Как отличаются по модулю архимедовы силы, действующие на кубики? Ответ обоснуйте. 

Архимедова сила для кубика 1 в 2 раза больше силы для кубика 2, так как объём погруженной в жидкость части кубика 1 в 2 раза больше объёма погруженной в жидкость части кубика 2.

Задание 51.3. Рассчитайте архимедову силу, действующую на камень объёмом $60 см^{3}$, полностью погруженный в воду.

Дано:
V = $60 см^{3}$;
$F_{A}$ − ?
СИ:
V = 0,00006 $м^{3}$;
Решение:
$F_{А} = gρ_{ж}V_{тж}$;
$ρ_{в} = 1000 кг/м^{3}$;
g ≈10 Н/кг;
$F_{А} = 10 * 1000 * 6 * 0,00006 = 0,6$ Н.
Ответ: 0,6 Н

Задание 51.4. Проделайте четыре виртуальных опыта с моделью «Выталкивающая сила как сумма контактных сил. Плавание тел», располагая в одной и той же жидкости кубики с ребром 20 см, изготовленные из разного материала. В каждом случае запишите в таблицу модули архимедовой силы $\overset{→}{F_{A}}$ и силы тяжести $\overset{→}{F_{тяж}}$, действующих на кубик. Проанализируйте результаты и сделайте вывод.

№ опыта           1                  2                 3                4
Вещество...    Алюминий Оргстекло Берёза Пенопласт
$F_{A}$, Н            80               80               80               80
$F_{тяж}$, Н         216             96               52                2
Вывод: во всех четырёх случаях архимедова сила одинакова, так как плотность жидкости, в которое погружено тело и объём погруженной части тела равны ($F_{А} = gρ_{ж}V_{т}$), а сила тяжести разная, потому что разная плотность веществ, из которых состоят тела (F= ρgV).

Задание 51.5. Кубик вначале подвесили на нити (рис. а), а затем опустили в сосуд с водой (рис. б).
а) Изобразите на обоих рисунках силы, действующие на кубик.

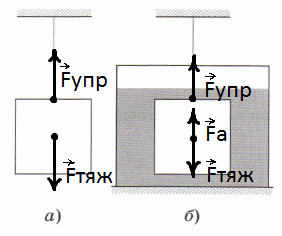
б) Впишите в текст недостающие буквы и знаки, чтобы получилось верное равенство.
Кубик в обоих случаях покоится, следовательно, равнодействующая сил, приложенных к кубику, в обоих случаях равна нулю:
рис. а: $R_{1} = F_{упр1} - F_{тяж} = 0$, отсюда $F_{упр1} = F_{тяж}$;

рис. б: $R_{2} = F_{упр2} + F_{A} - F_{тяж}$= 0,
отсюда $F_{упр2} = F_{тяж} - F_{A}$

Задание 51.6. Алюминиевый кубик массой 2,7 кг, подвешенный на нити, вначале погружён в воду полностью (рис. а), а затем наполовину (рис. б). Чему равна сила упругости нити в обоих случаях?

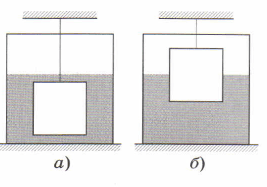
а) Дано:
m = 2,7 кг.
$F_{упр}$ − ?
Решение:
$F_{упр} = F_{тяж} - F_{A}$;
$F_{тяж}= mg$;
$F_{тяж}$= 2,7 * 10 = 27 Н;
$F_{А} = gρ_{ж}V_{т}$,
$V=\frac{m}{ρ}$;
$ρ_{ал}$ = 2700 кг/$м^{3}$;
$V=\frac{2,7}{2700} = 0,001 м^{3}$;
$ρ_{в}$ = 1000 кг/$м^{3}$;
$F_{А} = 10* 1000 * 0,001 = 10$ Н.
$F_{упр} = 27 - 10 = 17$ Н.
Ответ:17 Н.

б) Дано:
m = 2,7 кг;
$V_{погр} = \frac{1}{2}V_{т}$
$F_{упр}$ − ?
Решение:
$F_{упр} = F_{тяж} - F_{A}$;
$F_{тяж}= mg$;
$F_{тяж}$= 2,7 * 10 = 27 Н;
$F_{А} = gρ_{ж}V_{погр}$,
$V=\frac{m}{ρ}$;
$ρ_{ал}$ = 2700 кг/$м^{3}$;
$V=\frac{2,7}{2700} = 0,001 м^{3}$;
$ρ_{в}$ = 1000 кг/$м^{3}$;
$F_{А} = 10* 1000 * \frac{1}{2}*0,001 = 5$ Н.
$F_{упр}$ = 27 − 5 = 22 Н.
Ответ: 22 Н.