Тренировочный тест 7 "Закон Архимеда"

1. Одинаковые по размеру шарики опущены в разные жидкости: керосин, машинное масло и воду. При этом архимедовы силы, действующие на шарики со стороны жидкостей, между собой соотносятся следующим образом:
1) $F_{к} = F_{м} < F_{в}$
2) $F_{к} = F_{м} = F_{в}$
3) $F_{к} <F_{м} < F_{в}$
4) $F_{к} > F_{м} > F_{в}$

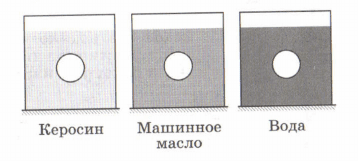
3) $F_{к} <F_{м} < F_{в}$

$F_{А} =ρ_{ж} gV_{т}$,
$F_{к} = 800gV_{т}$
$F_{м} = 900gV_{т}$
$F_{в} = 1000gV_{т}$

2. Три кубика одинакового размера, изготовленных их разных материалов ($ρ_{1}>ρ_{2}>ρ_{3}$) опущены в воду. При этом архимедовы силы, действующие на эти кубики со стороны жидкости, между собой соотносятся следующим образом
1) $F_{1} = F_{2} < F_{3}$
2) $F_{1} = F_{2} > F_{3}$
3) $F_{1} <F_{2} < F_{3}$
4) $F_{1} > F_{2} > F_{3}$

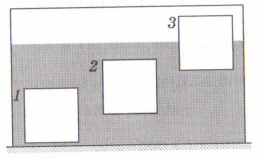
2) $F_{1} = F_{2} > F_{3}$

$F_{А} =ρ_{ж} gV_{т}$,
$F_{1} =ρ_{ж} gV_{т}$,
$F_{2} =ρ_{ж} gV_{т}$,
$F_{3} =ρ_{ж} g\frac{V_{т}}{2}$.

3. Железная гайка объемом 5 $см^{3}$ находится в сосуде с водой. Какова архимедова сила, действующая на гайку?
1) $3,9 * 10^{-2}$ Н
2) $4,9 * 10^{-2}$ Н
3) $38,2 * 10^{-2}$ Н
4) $50,0 * 10^{-2}$ Н

2) $4,9 * 10^{-2}$ Н

$F_{А} =ρ_{ж}gV_{т} = 1000 кг/м^{3} * 9,8 Н/кг * 0,000005 м^{3} = 0,049 Н = 4,9 * 10^{-2}$ Н

4. Брусок, верхняя грань которого касается поверхности жидкости, начинают равномерно поднимать из жидкости. На каком из графиков правильно показана зависимость выталкивающей силы $F_{A}$, действующей на брусок, от времени t?

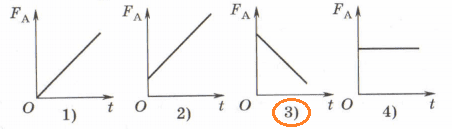
3)

5. Воздушный шарик объемом 2 $дм^{3}$ заполнен водородом плотностью 0,09 кг/$м^{3}$. Плотность окружающего шар воздуха 1,29 кг/$м^{3}$ . Максимальная масса оболочки шарика, чтобы он мог взлететь, равна
1) 2,4 г
2) 4,2 г
3) 6,0 г
4) 8,2 г

1) 2,4 г

$m=\frac{F}{g}$;
$F = F_{A} - P$
$F_{А} = gρ_{возд}V_{ш}$;
$P = mg = gρ_{вод}V_{ш}$;
$F = gρ_{возд}V_{ш} - gρ_{вод}V_{ш} = gV_{ш}(ρ_{возд} -ρ_{вод}) = 9,8 Н/кг * 0,002 м^{3} * (1,29 кг/м^{3} - 0,09 кг/м^{3})$ = 0,0024 кг = 2,4 г

6. Воздушный шар объемом 50 $м^{3}$ наполнили гелием плотностью 0,2 кг/$м^{3}$. Плотность окружающего шар воздуха равна 1,3 кг/$м^{3}$. Масса оболочки шара 10 кг. Максимальная масса груза, который этот шар сможет поднять, равна
1) 20 кг
2) 35 кг
3) 40 кг
4) 45 кг

4) 45 кг

$F_{A} = F_{т}$
$F_{A} = gρ_{возд}V_{ш}$;
$F_{т} = mg = (m_{1} + m_{2} + m_{3})g$, где $m_{1}$ − масса оболочки, $m_{2}$ − масса груза, $m_{3}$ − масса гелия.
$gρ_{возд}V_{ш} = (m_{1} + m_{2} + m_{3})g$
$m_{2} = ρ_{возд}V_{ш} - m_{1} - ρ_{г}V_{ш}= 1,3 кг/м^{3} * 50 м^{3} - 10 кг - 0,2 кг/м^{3} * 50 м^{3} = 45$ кг