Столики в кафе (из старого банка ФИПИ)

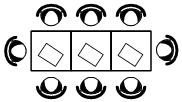
В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 16 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.
По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 16 член прогрессии:
a₁₆= 4 + 2 * (16 - 1) = 34.

Ответ: 34

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (16 - 2) * 2 = 6 + 28 = 34 человека.

Ответ: 34

5A3DF7

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 21 квадратный столик вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 21 член прогрессии:
a₂₁= 4 + 2 * (21 - 1) = 44.

Ответ: 44

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (21 - 2) * 2 = 6 + 38 = 44 человека.

Ответ: 44

D0F50E

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 19 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 19 член прогрессии:
a₁₉= 4 + 2 * (19 - 1) = 40.

Ответ: 40

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (19 - 2) * 2 = 40 человек.

Ответ: 40

17ABB5

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 20 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 20 член прогрессии:
a₂₀= 4 + 2 * (20 - 1) = 42.

Ответ: 42

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (20 - 2) * 2 = 42 человека.

Ответ: 42

97D5B4

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 18 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 18 член прогрессии:
a₁₈= 4 + 2 * (18 - 1) = 38.

Ответ: 38

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (18 - 2) * 2 = 38 человека.

Ответ: 38

A21B12

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 15 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 15 член прогрессии:
a₁₅= 4 + 2 * (15 - 1) = 32.

Ответ: 32

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (15 - 2) * 2 = 32 человека.

Ответ: 32

B26F2E

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 23 квадратных столика вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 23 член прогрессии:
a₂₃= 4 + 2 * (23 - 1) = 48.

Ответ: 48

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (23 - 2) * 2 = 48 человека.

Ответ: 48

27A42B

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 24 квадратных столика вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 24 член прогрессии:
a₂₄= 4 + 2 * (24 - 1) = 50.

Ответ: 50

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (24 - 2) * 2 = 50 человек.

Ответ: 50

922753

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 17 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 17 член прогрессии:
a₁₇= 4 + 2 * (17 - 1) = 36.

Ответ: 36

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (17 - 2) * 2 = 36 человек.

Ответ: 36

DF0BE2

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 22 квадратных столика вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 22 член прогрессии:
a₂₂= 4 + 2 * (22 - 1) = 46.

Ответ: 46

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (22 - 2) * 2 = 46 человек.

Ответ: 46

A907EE