Страница 24. Урок 10 Решение задач

9. Выполни действия. Объясни, почему каждое из полученных чисел может быть «лишним».

   72   
 – 16   56
   : 8    7
· 100   700
  : 14   50
    ?

900
: 30    30
– 12   18
+ 34   52
· 2     104
?

16    
· 4    64
– 7    57
: 19   3
· 150  450
?

78
: 6    13
· 4    52
+ 28 80
· 4    320
?

120
: 10    12
· 7      84
– 59    25
· 20    500
?

10. На выставку привели 156 собак четырёх пород: пуделей, шнауцеров, колли и спаниелей. Пуделей было 24, шнауцеров – в 3 раза больше, чем пуделей, а колли – на 38 меньше, чем шнауцеров. Сколько спаниелей привели на выставку? На сколько шнауцеров было больше, чем спаниелей?
Что ещё можно спросить?

1) 24*3 = 72 (шн.) - на выставке
2) 72-38 = 34 (кол.) - на выставке
3) 156 - (24+72+34 = 26 (спан.) - на выставке
4) 72 - 26 = 46 (шн.) - на столько было больше, чем спаниелей.
Ответ: 26 спаниелей и на 46 шнауцеров было больше, чем спаниелей.

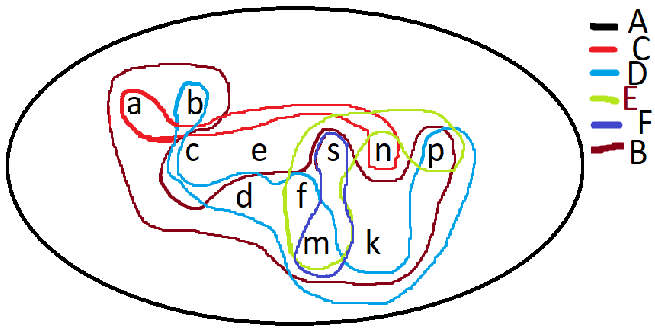
11. Найди прямые углы многоугольников. Составь множества А, В, C, D, E и F, запиши их с помощью фигурных скобок. Построй диаграмму Эйлера–Венна этих множеств.

А – множество многоугольников A {a; b; c; e; d; f; m; k; s; n; p}
В – множество многоугольников, имеющих хотя бы один прямой угол  B {a; b; d; f; m; k; s; p}
C – множество треугольников C {a; n;}
D – множество четырёхугольников D { b; d; f; m; s; p}
E – множество прямоугольников E { f; m; s; p}
F – множество квадратов F {m; s; }