Ответы к странице 134
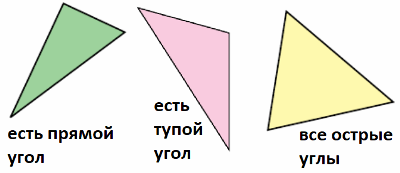
42. Начертите три треугольника со сторонами разной длины так, чтобы в одном треугольнике был прямой угол, в другом — тупой угол, а в третьем — все углы были острыми.
Решение:
43. В конкурсе детской песни участвовали шестеро четвероклассников — Андреев, Серова, Павлов, Васильев, Белов и Галкина. На диаграмме показано, сколько баллов получил каждый из них. Кто из участников конкурса получил наибольшее число баллов и кто — наименьшее? Сколько баллов получила каждая из девочек? Сколько баллов получил Павлов? Кто получил больше баллов — Галкина или Васильев — и на сколько?
Решение:
сколько баллов получил каждый из них.
Галкина 4
Белов 3
Серова 6
Андреев 10
Павлов 8
Васильев 5
Кто из участников конкурса получил наибольшее число баллов и кто — наименьшее?
Наибольшее Андреев 10
Наименьшее Белов 3
Сколько баллов получила каждая из девочек?
Галкина 4
Серова 6
Сколько баллов получил Павлов?
Павлов 8
Кто получил больше баллов — Галкина или Васильев — и на сколько?
Васильев больше на 1 балл.
44. Из данных чисел 0, 1, 2, 3, 4, 5, 6, 7, 8 укажите те, которые являются значениями x в неравенствах.
x < 3 x : 2 < 5
x > 4 3 · x > 10
Решение:
x < 3 {0, 1, 2}
x > 4 {0, 1, 2, 3}
x : 2 < 5 {0, 1, 2, 3, 4, 5, 6, 7, 8}
3 · x > 10 {0, 1, 2, 3}