Ответы к странице 98

3. Постройте отрезок произвольной длины и разделите его пополам с помощью циркуля и линейки.

Решение: 

Используем алгоритм:
1. Выберем раствор для радиуса окружности, чуть меньше длины отрезка, так чтобы он был гарантировано больше его половины.
2. Начертим две окружности, с центром в точках начала и конца отрезка.
3. Поставим точки пересечения окружностей.
4. Проведем отрезок по точкам пересечения окружностей.
5. Точка пересечения построенного отрезка и имеющегося и будет серединой имеющегося отрезка.

4. Как с помощью циркуля и линейки разделить отрезок: 1) на 4 равные части; 2) на 8 равных частей?

Решение: 

Делим отрезок пополам, потом еще пополам, это будет 4 часть.
Делим отрезок пополам, потом еще пополам, потом еще пополам, это будет 8 часть.

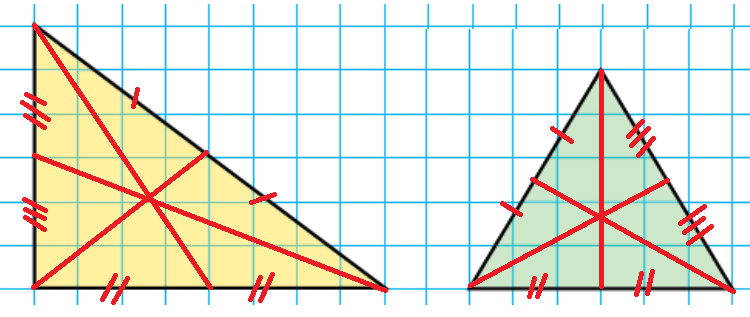
5. Постройте в тетради такие треугольники. Разделите каждую из сторон треугольника пополам и отметьте точками середины сторон. Соедините отрезком каждую отмеченную точку с противолежащей вершиной треугольника. Что вы заметили? Проверьте замеченное свойство на любом другом треугольнике. Для этого начертите треугольник со сторонами любой длины и выполните аналогичные построения.

Решение: 

Заметили, что образуются биссектрисы. Все они пересекаются в одной точке, все они делят угол у вершины пополам.

6. Не выполняя указанных действий, прикиньте, больше или меньше числа 1 000 результаты действий.
2 475 – 876 903 · 20
603 + 495 4 270 : 70

Решение: 

2 475 – 876 больше
603 + 495 больше
903 · 20 больше
4 270 : 70 меньше