Задание № 1120
Сила тока в проводнике сопротивлением $R_{1} = 10$ Ом равна 2 А (рис. 173). Чему равно сопротивление $R_{2}$ проводника, если сила тока в неразветвлённой части цепи (показания амперметра) 3 А?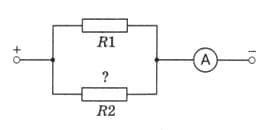 рис. 173
рис. 173
Решение
Дано:
$R_{1} = 10$ Ом;
$I_{1} = 2$ А;
I = 3 А.
Найти:
$R_{2}$ − ?
Решение:
Найдем напряжение по закону Ома:
$U_{1} = I_{1}R_{1}$;
$U_{1} = 2 * 20 = 20$ В;
Напряжение в цепи и на концах всех параллельно соединённых проводников одно и то же:
$U_{1} = U_{2} = U = 20$ В;
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
$I = I_{1} + I_{2}$;
$I_{2} = I - I_{1}$;
$I_{2} = 3 - 2 = 1$ А;
Найдем сопротивление по закону Ома:
$R_{2} = \frac{U}{I_{2}}$;
$R_{2} = \frac{20}{1} = 20$ Ом.
Ответ: 20 Ом.
Задание № 1121
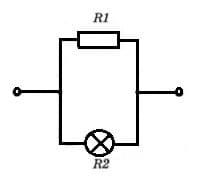
В сеть напряжением 220 В включены параллельно лампа и плитка, сопротивления которых соответственно равны 240 и 60 Ом. Найдите силу тока в каждом потребителе тока и в проводах, подводящих ток в квартиру. Начертите схему цепи.
Решение
Дано:
U = 220 В;
$R_{1} = 240$ Ом;
$R_{2} = 60$ Ом.
Найти:
I − ?
$I_{1}$ − ?
$I_{2}$ − ?
Решение:
Сопротивление цепи при параллельном соединении:
$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$;
$R = \frac{R_{1} * R_{2}}{R_{1} + R_{2}}$;
$R = \frac{240 * 60}{240 + 60} = 48$ Ом;
Напряжение в цепи и на концах всех параллельно соединённых проводников одно и то же:
$U = U_{1} = U_{2} = 220$ В;
Найдем силу тока по закону Ома:
$I = \frac{U}{R} = \frac{220}{48} = 4,6$ А;
$I = \frac{U}{R_{1}} = \frac{220}{240} = 0,9$ А;
$I = \frac{U}{R} = \frac{220}{60} = 3,7$ А.
Ответ: 4,6 А; 0,9 А; 3,7 А.
Задание № 1122
Рассчитайте силу тока в лампе и её сопротивление по схеме, изображённой на рисунке 174.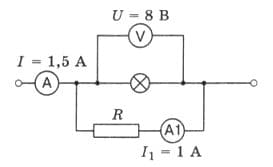 рис. 174
рис. 174
Решение
Дано:
I = 1,5 А;
$U_{л} = 8$ В;
$I_{1} = 1$ А.
Найти:
$R_{л}$ − ?
$I_{л}$ − ?
Решение:
При параллельном соединении сила тока в подводящих проводах равна сумме сил тока в лампе и проводнике:
$I = I_{1} +I_{л}$;
$I_{л} = I - I_{1}$;
$I_{л} = 1,5 - 1 = 0,5$ А;
Напряжение на лампе и на проводнике равно напряжению сети, т.к. лампа и проводник соединены параллельно.
$U_{л} = U_{1} = U = 8$ В;
Найдем сопротивление лампы по закону Ома:
$R_{л} = \frac{U}{I_{л}}$;
$R_{л} = \frac{8}{0,5} = 16$ Ом.
Ответ: 0,5 А; 16 Ом.
Задание № 1123
Чтобы автомобильная лампа не перегорела, силу тока через неё следует ограничить до 4 А. Испытания показали, что при подключении лампы к источнику тока с напряжением 12 В надо включить последовательно с лампой проводник сопротивлением 1 Ом. Чему равно сопротивление лампы?
Решение
Дано:
$I_{1} = 4$ А;
U = 12 В;
$R_{2} = 1$ Ом.
Найти:
$R_{1}$ − ?
Решение:
Сила тока при последовательном соединении проводников одинаковая:
$I_{1} = I_{2} = I = 4$ А.
Найдем сопротивление цепи по закону Ома:
$R = \frac{U}{I}$;
$R = \frac{12}{4} = 3$ Ом.
Сопротивление цепи при последовательном соединении проводников:
$R = R_{1} + R_{2}$;
$R_{1} = R - R_{2}$;
$R_{1} = 3 - 1 = 2$ Ом.
Ответ: 2 Ом.
Задание № 1124
Определите силу тока в каждом резисторе, если напряжение на всём участке цепи равно 4 В (рис. 175).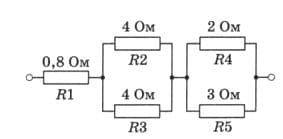 рис. 175
рис. 175
Решение
Дано:
$R_{1} = 0,8$ Ом;
$R_{2} = 4$ Ом;
$R_{3} = 4$ Ом;
$R_{4} = 2$ Ом;
$R_{5} = 3$ Ом;
U = 4 В.
Найти:
$I_{1}$ − ?
$I_{2}$ − ?
$I_{3}$ − ?
$I_{4}$ − ?
$I_{5}$ − ?
Решение:
Резисторы $R_{2}$ и $R_{3}$, $R_{4}$ и $R_{5}$ соединены параллельно.
Резисторы $R_{1}, R_{23}, R_{45}$ соединены последовательно.
Сопротивление в резисторах при параллельном соединении:
$R_{23} = \frac{R_{2} * R_{3}}{R_{2} + R_{3}}$;
$R_{23} = \frac{4 * 4}{4 + 4} = 2$ Ом;
$R_{45} = \frac{R_{4} * R_{5}}{R_{4} + R_{5}}$;
$R_{45} = \frac{2 * 3}{2 + 3} = 1,2$ Ом;
Сопротивление цепи при последовательном соединении:
$R = R_{1} + R_{23} + R_{45}$;
R = 0,8 + 2 + 1,2 = 4 Ом.
Найдем силу тока в цепи по закону Ома:
$I = \frac{U}{R}$;
$I = \frac{4}{4} = 1$ А;
Сила тока при последовательном соединении резисторов одинаковая:
$I = I_{1} = I_{23} = I_{45} = 1$ А.
Сила тока при параллельном соединении:
$I_{2} = I_{3} = \frac{I_{23}}{N} = \frac{1}{2} = 0,5$ А;
Найдем напряжение по закону Ома:
$U_{45} = I * R_{45}$;
$U_{45} = 1 * 1,2 = 1,2$ В;
Напряжение на резисторах $R_{4}$ и $R_{5}$ равно напряжению сети на участке $R_{45}$, т.к. они соединены параллельно.
$U_{45} = U_{4} = U_{5} = 1,2 В$;
Найдем силу тока по закону Ома:
$I_{4} = \frac{U_{4}}{R_{4}} = \frac{1,2}{2} = 0,6$ А;
$I_{5} = \frac{U_{5}}{R_{5}} = \frac{1,2}{3} = 0,4$ А.
Ответ: 1 А; 0,5 А; 0,5 А; 0,6 А; 0,4 А.
Задание № 1125
По рисунку 176 определите силу тока в каждом резисторе и напряжение на всём участке цепи.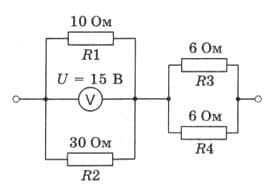 рис. 176
рис. 176
Решение
Дано:
$R_{1} = 10$ Ом;
$R_{2} = 30$ Ом;
$R_{3} = 6$ Ом;
$R_{4} = 6$ Ом;
$U_{12} = 15$ В.
Найти:
$I_{1}$ − ?
$I_{2}$ − ?
$I_{3}$ − ?
$I_{4}$ − ?
U − ?
Решение:
Резисторы $R_{1}$ и $R_{2}$, $R_{3}$ и $R_{4}$ соединены параллельно.
Резисторы $R_{12}, R_{34}$ соединены последовательно.
Напряжение на резисторах $R_{1}$ и $R_{2}$ равно напряжению сети на участке $R_{12}$, т.к. они соединены параллельно.
$U_{12} = U_{1} = U_{2} = 15 В$;
Найдем силу тока по закону Ома:
$I_{1} = \frac{U_{1}}{R_{1}} = \frac{15}{10} = 1,5$ А;
$I_{2} = \frac{U_{2}}{R_{2}} = \frac{15}{30} = 0,5$ А.
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
$I_{12} = I_{1} + I_{2}$;
$I_{12} = 1,5 + 0,5 = 2$ А.
Сила тока при последовательном соединении резисторов одинаковая:
$I = I_{12} = I_{34} = 2$ А.
Сила тока при параллельном соединении:
$I_{3} = I_{4} = \frac{I_{34}}{N} = \frac{2}{2} = 1$ А;
Сопротивление в резисторах при параллельном соединении:
$R_{34} = \frac{R_{3} * R_{4}}{R_{3} + R_{4}}$;
$R_{34} = \frac{6 * 6}{6 + 6} = 3$ Ом;
Напряжение найдем по закону Ома:
$U_{34} = I_{34} * R_{34}$;
$U_{34} = 2 * 3 = 6$ В;
Напряжение на всем участке цепи при последовательном соединении:
$U = U_{12} + U_{34}$;
U = 15 + 6 = 21 В.
Ответ: 1,5 А; 0,5 А; 1 А; 1 А; 21 В.

