Задание №1755
Используя закон сохранения энергии, решите задачу Гюйгенса: докажите, что «подвешенный на нити к центру вертикального круга шар не может вращаться по этому кругу, если нить не в состоянии выдержать силу натяжения, превышающую вес шара в 6 раз».
Решение
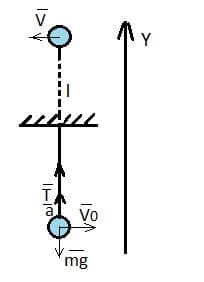 Изобразим все силы, действующие на шар: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$.
Изобразим все силы, действующие на шар: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{ma} = \overset{→}{mg} + \overset{→}{T}$;
Выберем ось Y перпендикулярно горизонтальной плоскости. Спроецируем уравнение на координатные оси:
T − mg = ma;
$a_{ц} = \frac{v_{0}^{2}}{l}$;
$T = ma + mg = \frac{mv_{0}^{2}}{l} + mg$;
По закону сохранения механической энергии:
$E_{к0} = E_{п} + E_{к}$;
$E_{к0} = \frac{mv_{0}^{2}}{2}$;
$E_{к} = \frac{mv^{2}}{2}$;
$E_{п} = mg * 2l$;
$\frac{mv_{0}^{2}}{2} = mg * 2l + \frac{mv^{2}}{2}$;
Шар движется по дуге окружности. В верхней точке:
$a = \frac{v^{2} }{l} = g$;
В этой точке на шар действует только сила тяжести. Поэтому:
$v^{2} = gl$;
$\frac{mv_{0}^{2}}{2} = 2mgl + \frac{mgl}{2} = \frac{5mgl}{2}$;
$v_{0}^{2} = \frac{ \frac{5mgl}{2}}{\frac{m}{2} } = 5gl$;
$T = \frac{5glm}{l} + mg = 6mg = 6P$;
Вывод: «подвешенный на нити к центру вертикального круга шар не может вращаться по этому кругу, если нить не в состоянии выдержать силу натяжения, превышающую вес шара в 6 раз» (T = 6P).
Задание №1756
Древнейшее из дошедших до нас сочинений по механике называется «Механические проблемы». Оно создано в Египте в III в. до н.э. В нём есть такая задача: «Почему, если к дереву приложить топор, обременённый тяжёлым грузом, то дерево будет повреждено весьма незначительно, но если поднять топор без груза и ударить по дереву, то оно расколется? Между тем падающий груз в этом случае гораздо меньше давящего». Автор сочинения не мог ответить на поставленный вопрос. А что ответите вы?
Решение
Потому что падающий топор, кроме потенциальной энергии, обладает кинетической энергией, которая значительно превышает потенциальную энергию тяжёлого груза, а на топор.
Задание №1757
На рисунке 274 изображена «чёртова петля», которая была изобретена в 1902 г. одновременно двумя цирковыми артистами − Дьяволо (Джонсоном) и Мефисто (Нуазеттом). По этой петле цирковые артисты спускаются на велосипеде на глазах изумлённой публики. С какой наименьшей высоты должен начинать движение артист, чтобы не упасть с петли в её верхней части?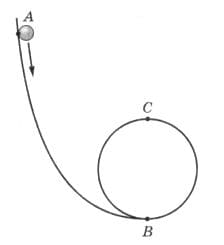 рис. 274
рис. 274
Решение
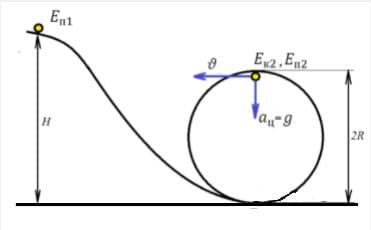 По закону сохранения полной механической энергии:
По закону сохранения полной механической энергии:
$E_{1} = E_{2}$;
$E_{1}$ − полная энергия артиста и велосипеда в начале движения, где скорость артиста равна нулю.
$E_{2}$ − полная энергия артиста с велосипедом в верхней точке "колеса" (т. С).
$E_{1} = E_{п1} = mgh$;
$E_{2} = E_{п2} + E_{к2} = mg * 2R + \frac{mv^{2}}{2}$;
Поскольку центростремительное ускорение в верхней точке равно силе тяжести, то
$ma_{ц} = \frac{mv^{2}}{R} = mg$;
$mv^{2} = mgR$;
$E_{2} = mg * 2R + \frac{mgR}{2} = \frac{5mgR}{2}$;
$mgh = \frac{5mgR}{2}$;
$h = \frac{5R}{2} = 2,5 R$.
Ответ: 2,5 R.
Задание №1758
Тело массой m спустилось по наклонной плоскости без трения с высоты h. Какова скорость тела в конце движения? Какова была бы скорость этого тела, если бы оно свободно упало на землю с высоты h?
Решение
По закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
Кинетическая энергия в начальной точке и потенциальная энергия в конечной точке равны нулю, т.е. при соскальзывании потенциальная энергия тела вблизи пола полностью переходит в кинетическую энергию. Значит:
$E_{п1} = E_{к2}$;
$mgh = \frac{mv^{2}}{2}$;
$2mgh = mv^{2}$;
$v^{2} = \frac{2mgh}{m} = 2gh$;
$v = \sqrt {2gh}$.
Аналогично при падении тела с высоты действует закон сохранения энергии.
$E_{п1} = E_{к2}$;
$mgh = \frac{mv^{2}}{2}$;
$2mgh = mv^{2}$;
$v^{2} = \frac{2mgh}{m} = 2gh$;
$v = \sqrt {2gh}$.
Таким образом, скорость тела в конце спуска по наклонной плоскости и в момент соприкосновения с землей при свободном падении равна $\sqrt {2gh}$.
Ответ: $\sqrt {2gh}$.
Задание №1759
Тело брошено под углом α к горизонту с начальной скоростью v. На какой высоте его кинетическая и потенциальная энергии будут равными?
Решение
Дано:
α;
v;
$E_{п} = E_{к}$.
Найти:
h − ?
Решение:
В момент начала движения $h_{0} = 0$, значит $E_{п} = 0$.
По закону сохранения механической энергии:
$E_{к0} = E_{п} + E_{к}$;
Из условия равности кинетической и потенциальной энергии $E_{п} + E_{к} = 2E_{п}$.
$E_{к0} = 2E_{п}$;
$\frac{mv^{2}}{2} = 2mgh$;
$v^{2} = 4 gh$;
$h = \frac{v^{2}}{4g}$.
Ответ: $\frac{v_{0}^{2}}{4g}$.
Задание №1760
Человек, прыгая с высоты, в момент приземления как бы пружинит. Докажите, используя закон сохранения механической энергии, что, чем больше путь торможения человека, тем меньше сила удара.
Решение
При падении тела с высоты действует закон сохранения энергии.
$E_{п1} = E_{к2}$;
$mgH = \frac{mv^{2}}{2}$;
$2mgH = mv^{2}$;
$v^{2} = \frac{2mgH}{m} = 2gH$;
Среднее ускорение, возникающее в процессе остановки тела, движущегося со скоростью v на пути h определяется из выражения:
$v^{2} = 2aH$;
gH = ah;
$a = \frac{gH}{h}$;
$F = ma = \frac{mgH}{h}$,
$\frac{H}{h}$ − отношение высоты падения к расстоянию, на котором происходит торможение тела до полной остановки.
Таким образом, чем больше путь торможения человека, тем меньше сила удара.
Задание №1761
Докажите, что при одинаковой начальной скорости тормозной путь гружёного и не гружёного автомобилей одинаков. Считать постоянным коэффициент сопротивления движению.
Решение
Дано:
$v_{1} = v_{2}$;
$m_{1} > m_{2}$;
μ = const.
Доказать:
$S_{1} = S_{2}$;
Доказательство:
Процесс торможения автомобиля выглядит как закон сохранения энергии:
$E_{к} = A_{тр}$,
т.е. кинетическая энергия машины с массой m и и скоростью v при торможении переходит в тепло за счет работы силы трения $F_{тр}$, которая затрачивается на замедление машины на участке пути длиной S.
$E_{к}= \frac{mv^{2}}{2}$
$A_{тр} = F_{тр} * S$;
$F_{тр} = μmg$;
$\frac{mv^{2}}{2} = μmgS$;
$\frac{v^{2}}{2} = μgS$;
$S = \frac{v^{2}}{2μg}$.
Таким образом, если $v_{1} = v_{2}$, то $S_{1} = S_{2}$.

