Задание №599
Определите КПД рычага, с помощью которого груз массой 80 кг был поднят на высоту 0,9 м. При этом большее плечо рычага, к которому была приложена сила 500 Н, опустилось на 1,8 м.
Решение
Дано:
$h_{1} = 1,8$ м;
$h_{2} = 0,9$ м;
m = 80 кг;
F = 500 Н.
Найти:
η − ?
Решение:
$А_{п} = Fh_{2} = mgh_{2}$;
$А_{з} = Fh_{1}$;
$η =\frac{А_{п}}{А_{з}} * 100 = \frac{mgh_{2}}{Fh_{1}} * 100$ %;
g ≈10 Н/кг;
$η =\frac{80 * 10 * 0,9}{500 * 1,8} * 100 = 80$ %.
Ответ: 80 %.
Задание №600
С помощью неподвижного блока, имеющего КПД 90% , груз массой 100 кг подняли на высоту 1,5 м. Определите совершённую при этом работу.
Решение
Дано:
η = 90 %;
h= 1,5 м;
m = 100 кг.
Найти:
$А_{з}$ − ?
Решение:
Неподвижный блок не дает выигрыша в силе и расстоянии.
$А_{п} = Fh = mgh$;
$η =\frac{А_{п}}{А_{з}} * 100$ %;
$А_{з} = \frac{А_{п}}{η} * 100 = \frac{mgh}{η} * 100$ %;
g ≈10 Н/кг;
$η =\frac{100 * 10 * 1,5}{90} * 100 = 1667$ Дж.
Ответ: 1,667 Дж.
Задание №601
Груз массой 20 кг равномерно тянут вдоль наклонной плоскости, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости, если её длина 2 м, а высота 10 см?
Решение
Дано:
l = 2 см;
h = 10 cм;
m = 20 кг;
F = 40 Н.
Найти:
η − ?
СИ:
l = 0,02 м;
h = 0,1 м;
Решение:
$А_{п} = Fh= mgh$;
$А_{з} = Fl$;
$η =\frac{А_{п}}{А_{з}} * 100 = \frac{mgh}{Fl} * 100$ %;
g ≈10 Н/кг;
$η =\frac{20 * 10 * 0,1}{40 * 0,02} * 100 = 25$ %.
Ответ: 25 %.
Задание №602
Вычислите опытным путём, какой выигрыш в силе дают ножницы, плоскогубцы, кусачки.
Решение
Рукоятка ножниц, плоскогубцев, кусачек и лезвия являются разными плечами рычага. Варьируя длиной рукоятки и лезвия, мы получаем выигрыш в силе.
$\frac{F_{1}}{ F_{2}} = \frac{l_{2}}{ l_{1}} $ − условие равновесия рычага.
Измерим длину рукоятки и лезвия. Выигрышем будет соотношение длины рукояток к длине лезвий.
Задание №603
Грузы сдвигают с места с помощью палки (рис. 89). Какой из грузов сдвинется с места? Почему? Проверьте на опыте. рис. 89
рис. 89
Решение
Оба груза сдвинутся с места. Палка действует на эти грузы как рычаг.
Задание №604
Возьмите спичку и переломите её пополам. Если вы попробуете теперь каждую из половинок переломить снова, то убедитесь, что сделать это гораздо труднее. Почему?
Решение
Спичка представляет с собой рычаг. Она ломается в точке опоры, под действием момента приложенной к ее краям силы. M = Fd.
Чем меньше длина спички, тем короче плечо рычага d, значит для создания одинакового момента силы, требуется приложить большую силу F.
Задание №605
«Дайте мне точку опоры, и я переверну мир» − такое заявление сделал Архимед после того, как открыл правило рычага. Поскольку подходящей точки опоры не было (да и сейчас нет), доказать это утверждение экспериментально он не мог. Однако теоретически нетрудно убедиться в том, что Архимед несколько переоценил свои возможности (и возможности рычага). Подсчитайте, на какое расстояние пришлось бы переместить свободный конец рычага, для того чтобы приподнять хотя бы на 1 см тело, масса которого равна массе Земли ($6 * 10^{24}$ кг).
Решение
Для подъема Земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например со скоростью 1 м/с, потребовались бы миллионы лет.
$\frac{F_{1}}{ F_{2}} = \frac{l_{2}}{ l_{1}} $;
$F_{1}l_{1} = F_{2}l_{2} = m_{2}gl_{2}$;
$l_{1} = \frac{m_{2}gl_{2}}{F_{1}}$;
$l_{1} = \frac{6 * 10^{24} * 10 * 0,01}{F_{1}} = \frac{6 * 10^{23}}{F_{1}}$.
Задание №606
Уже в глубокой древности для получения выигрыша в силе тяжёлый груз перемещали не по вертикали, а по наклонной плоскости. Этот способ широко применяли египтяне ещё в III в. до н.э. при постройке пирамид и установке обелисков. Покажите на опыте, какой выигрыш в силе даёт наклонная плоскость. Трением пренебречь.
Решение
Наклонная плоскость дает выигрыш в силе во столько раз, во сколько ее длина больше высоты.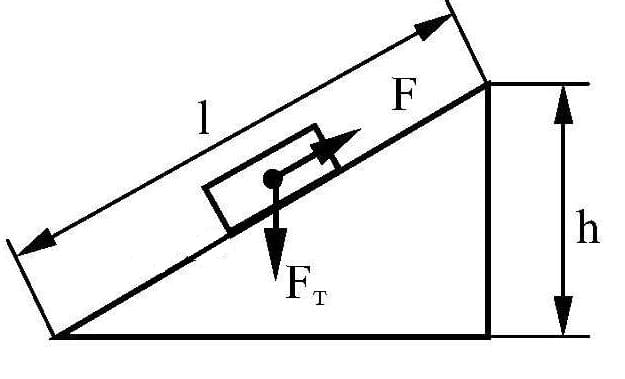 1. Пусть вес бруска равен P, сила тяги F.
1. Пусть вес бруска равен P, сила тяги F.
2. Закрепим доску в лапке штатива в наклонном положении.
4. Переместим брусок с постоянной скоростью вверх по наклонной доске.
6. Измерим с помощью линейки путь s, который проделал брусок. Он равен 0,4 м.
7. Измерим также высоту наклонной плоскости h, она равна 0,2 м.
В соответствии с "золотым правилом" механики:
$А_{п} = А_{з}$;
Ph = Fs;
$\frac{P}{F} = \frac{s}{h} = \frac{0,4}{0,2}$ = 2.
Наклонная плоскость при отсутствии силы трения дала бы выигрыш в силе в 2 раза.

