Задание №1397

Определите проекции векторов перемещения на ось х (рис. 216, а) и ось у (рис. 216, б).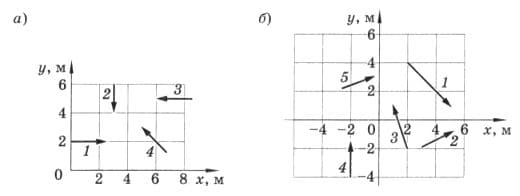

Решение

а)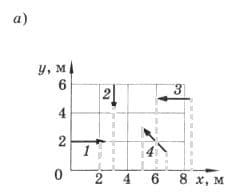 
Проекции векторов перемещения на ось х:
$s_{1} = x_{2} - x_{1} = 2 - 0 = 2$ м;
$s_{2} = x_{2} - x_{1} = 3 - 3 = 0$ м;
$s_{3} = x_{2} - x_{1} = 6 - 8,5 = -2,5$ м;
$s_{4} = x_{2} - x_{1} = 5-7 = -2 $ м.

б) 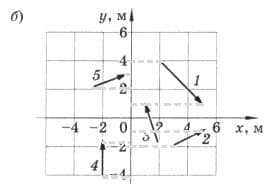Проекции векторов перемещения на ось y:
$s_{1} = y_{2} - y_{1} = 1 - 4 = - 3$ м;
$s_{2} = y_{2} - y_{1} = -1 - (-2) = 1$ м;
$s_{3} = y_{2} - y_{1} = 1 - (-2) = 3$ м;
$s_{4} = y_{2} - y_{1} = -2 - (-4) = 2$ м;
$s_{5} = y_{2} - y_{1} = 3 - 2 = 1$ м.

Задание №1398

Автобус совершил рейс по маршруту АВС (рис. 217). Определите графически пройденный автобусом путь и модуль перемещения.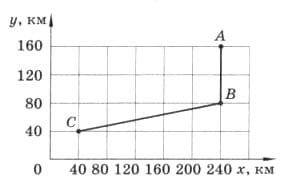
рис. 217

Решение

Дано:
$х_{1} = -1$ м;
$у_{1} = 2$ м;
$s_{х} = 3$ м;
$s_{y} = -4$ м.
Найти:
s − ?
|$\overset{→}{s}$| − ?
Решение: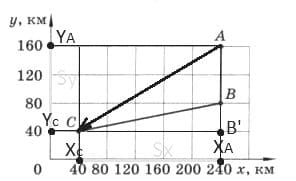
Перемещение тела (материальной точки) − вектор, соединяющий начальное положение тела с его последующим положением. Чтобы найти модуль перемещения тела нужно определить кратчайшие расстояние между точками A и С.
$s_{x} = x_{C} - x_{A}$;
$s_{x} = 40 - 240 = -200$ км;
$s_{y} = y_{C} - y_{A}$;
$s_{y} = 40 - 160 = -120$ км;
Найдем модуль перемещения:
|$\overset{→}{s}| = \sqrt{s_{x}^{2} + s_{y}^{2}}$;
|$\overset{→}{s}| = \sqrt{(-200)^{2} + (-120)^{2}} = 233$ км.
Пройденный путь равен сумме отрезков:
s = AB + BC;
AB = 160 − 80 = 80 км;
Найдем длину отрезка BC по теореме Пифагора:
BC = $\sqrt{BB'^{2} + B'C^{2}} = \sqrt{(80-40)^{2} + (240-40)^{2}} = 204$ км.
s = 80 + 204 = 284 км.
Ответ: 233 км; 284 км.

Задание №1399

Самолёт пролетел по прямой 400 км, затем повернул под углом 90° и пролетел ещё 300 км. Определите графически пройденный самолётом путь и модуль перемещения.

Решение

Дано:
AB = 400 км;
BC = 300 км;
∠B = 90°.
Найти:
s − ?
|$\overset{→}{s}$| − ?
Решение: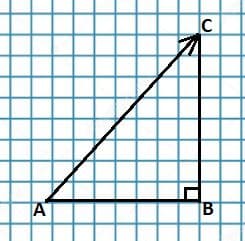
Пройденный путь равен сумме отрезков:
s = AB + BC;
AB = 400 + 300 = 700 км;
Так как ∠B = 90°, найдем перемещение по теореме Пифагора:
|$\overset{→}{s}$| = $\sqrt{AB^{2} + BC^{2}} = \sqrt{(400)^{2} + (300)^{2}} = 500$ км.
Ответ: 700 км; 500 км.

Задание №1400

Автомобиль, заправившись на АЗС бензином, движется прямолинейно. На расстоянии 20 км от АЗС он поворачивает и, пройдя в противоположном направлении 28 км, останавливается. Найдите модуль перемещения и пройденный автомобилем путь. Сделайте рисунок.

Решение

Дано:
$S_{1} = 20$ км;
$S_{2} = 28$ км.
Найти:
S − ?
|$\overset{→}{S}$| − ?
Решение: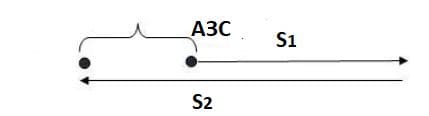
Перемещение тела − вектор, соединяющий начальное положение тела с его последующим положением. В нашем случае оно равно разнице путей.
$|\overset{→}{S}| = S_{2} - S_{1} = 28 - 20 = 8$ км;
Общий путь равен:
$S = S_{1} + S_{2}$;
S = 20 + 28 = 48 км.
Ответ: 8 км; 48 км.

Задание №1401

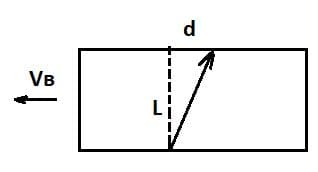
Вагон шириной 2,7 м был пробит пулей, летящей перпендикулярно движению вагона. Смещение отверстий в стенках вагона относительно друг друга равно 3 см. Чему равна скорость движения пули внутри вагона, если вагон движется со скоростью 36 км/ч?

Решение

Дано:
L = 2,7 м;
d = 3 см;
$v_{в} = 36$ км/ч.
Найти:
$v_{п}$ − ?
СИ:
d = 0,03 м;
$v_{в} = 10$ м/с.
Решение:
Расстояние, которое проехал поезд за время полета пули, равно:
$d = v_{в}t$;
$t = \frac{d}{v_{в}}$;
Скорость пули равна:
$v_{п} = \frac{L}{t} = \frac{L}{\frac{d}{v_{в}}} = \frac{Lv_{в}}{d}$;
$v_{п} = \frac{2,7 * 10}{0,03} = 900$ м/с.
Ответ: 900 м/с.

Задание №1402

Велосипедист едет равномерно со скоростью 24 км/ч, его обгоняет мотоциклист, движущийся со скоростью 20 м/с. Постройте графики скоростей движения велосипедиста и мотоциклиста.

Решение

Скорость велосипедиста в системе СИ:
$24 км/ч = \frac{24 * 1000}{3600} = 6,7$ м/с.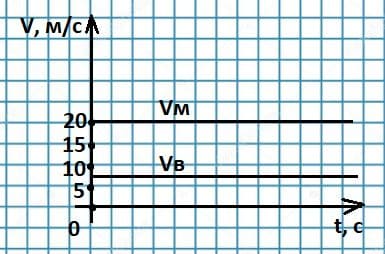

Задание №1403

На рисунке 218 изображены графики изменения координат двух тел. Чему равны модули скоростей этих тел? Опишите характер движения тел, напишите уравнения движения. Найдите расстояние между телами в начальный
момент времени.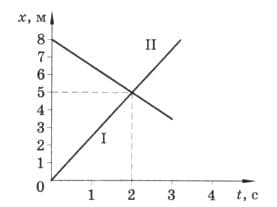
рис. 218

Решение

Тела движутся равномерно прямолинейно, навстречу друг другу.
Начальные координаты тел в момент времени t = 0:
$x_{0I} = 0 м; x_{0II} = 8$ м;
Координаты тел в момент встречи t = 2 с:
$x_{I} = x_{II} = 5$ м;
Для равномерного прямолинейного движения уравнение координаты:
$x = x_{o} + v_{x}t$;
$x - x_{o} = v_{x}t$;
$v_{x} = \frac{x - x_{o}}{t}$;
|$v_{xI}| = |\frac{5 - 0}{2}| = 2,5 $ м/с;
|$v_{xII}| = |\frac{5 - 8}{2}| = 1,5$ м/с;
Следовательно, уравнения движения:
$x_{I} = 2,5t$;
$x_{II} = 8 - 1,5t$;
$s = x_{0II} - x_{0I} = 8 - 0 = 8$ м.
Ответ: 2,5 м/с; 1,5 м/с; $x_{I} = 2,5t$; $x_{II} = 8 - 1,5t$; 8 м.