Задание №340
Напор воды (разность уровней воды до и после плотины) Саяно−Шушенской ГЭС равен 194 м. Какое давление испытывает плотина на такой глубине?
Решение
Дано:
h = 194 м;
$ρ_{в} = 1000 кг/м^{3}$;
Найти:
p − ?
Решение:
p = gρh;
g ≈10 Н/кг;
p = 10 * 1000 * 194 = 1 940 000 Па = 1,9 МПа.
Ответ: 1,9 МПа.
Задание №341
Какой напор воды (в м) имеет плотина Днепровской ГЭС, если вода оказывает давление 400 кПа?
Решение
Дано:
p = 400 кПа;
$ρ_{в} = 1000 кг/м^{3}$;
Найти:
h − ?
СИ:
$p = 4*10^{5}$ Па;
Решение:
p = gρh;
$h = \frac{p}{gρ}$;
g ≈10 Н/кг;
$h = \frac{4 * 10^{5}}{10 * 1000} = 40$ м;
Ответ: 40 м.
Задание №342
Жидкость нагнетают в цилиндр под давлением 400 кПа (рис. 27). Рассчитайте силу давления, действующую на поршень, площадь которого 250 $см^{2}$.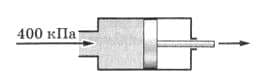 рис. 27
рис. 27
Решение
Дано:
p = 400 кПа;
S = 250 $см^{2}$
Найти:
F − ?
СИ:
p = 400 000 Па;
S = 0,025 $м^{2}$
Решение:
$p=\frac{F}{S}$;
F = pS;
F = 400 000 * 0,025 = 10 000 Н = 10 кН.
Ответ: 10 кН.
Задание №343
Какое боковое давление испытывает плотина Братской ГЭС на глубине 96 м? Какая сила действует на каждый квадратный метр поверхности плотины на этой глубине?
Решение
Дано:
h = 96 м;
$ρ_{в} = 1000 кг/м^{3}$;
S = 1 $м^{2}$
Найти:
p − ?
F − ?
Решение:
p = gρh;
g ≈10 Н/кг;
p = 10 * 1000 * 96 = 960 000 Па = 0,96 МПа.
$p=\frac{F}{S}$;
F = pS;
F = 960 000 * 1 = 960 000 Н = 0,96 МН.
Ответ: 0,96 МПа; 0,96 МН.
Задание №344
Давление в каждой из четырёх шин автомобиля 200 кПа. Чему равен вес автомобиля, если площадь соприкосновения шины с грунтом 500 $см^{2}$?
Решение
Дано:
$p_{1} = 200$ кПа;
$S_{1} = 500 см^{2}$;
Найти:
P − ?
СИ:
$p_{1} = 200 000$ Па;
$S_{1} = 0,05 м^{2}$;
Решение:
Давление 4−х шин равно:
$p=4 * \frac{P}{S}$;
P = 4pS;
P = 4 * 200 000 * 0,05 = 40 000 Н = 40 кН.
Ответ: 40 кН.
Задание №345
Чему равна сила давления на каждый квадратный дециметр поверхности тела человека, находящегося на глубине 6 м?
Решение
Дано:
h = 6 м;
$S = 1 дм^{2}$;
$ρ_{в} = 1000 кг/м^{3}$;
Найти:
F − ?
СИ:
$S = 0,01 м^{2}$;
Решение:
p = gρh;
g ≈10 Н/кг;
p = 10 * 1000 * 6 = 60000 Па;
$p=\frac{F}{S}$;
F = pS;
F = 60000 * 0,01 = 600 Н.
Ответ: 600 Н.
Задание №346
С какой силой давит вода на иллюминатор батискафа на глубине 1,5 км, если иллюминатор имеет форму круга диаметром 400 мм?
Решение
Дано:
h = 1,5 км;
d = 400 мм;
$ρ_{в} = 1030 кг/м^{3}$;
Найти:
F − ?
СИ:
h = 1500 м;
d = 0,4 м;
Решение:
p = gρh;
g ≈10 Н/кг;
p = 10 * 1030 * 1500 = 15 450 000 Па;
$p=\frac{F}{S}$;
F = pS;
$S = \frac{πd^{2}}{4}$;
$S = \frac{3,14 * 0,4^{2}}{4} = 0,1256 м^{2}$;
F = 15 450 000 * 0,1256 = 1 940 520 Н = 1,9 МН.
Ответ: 1,9 МН.
Задание №347
Бак объёмом 1 $м^{3}$, имеющий форму куба, заполнен нефтью. Определите силу давления нефти на дно бака.
Решение
Дано:
V = 1 $м^{3}$;
$ρ_{н} = 800 кг/м^{3}$;
Найти:
F − ?
Решение:
$p=\frac{F}{S}$;
p = gρh;
$\frac{F}{S} = gρh$
F = gρV;
g ≈10 Н/кг;
F = 10 * 800 * 1 = 8000 Н = 8 кН.
Ответ: 8 кН.
Задание №348
В сосуде под поршнем находится глицерин, высота уровня которого 40 см. Вес поршня 5Н, а его площадь 20 $см^{2}$. Определите:
а) давление глицерина на дно сосуда;
б) боковое давление на уровне 30 см.
Решение
а) Дано:
h = 40 см;
$P_{п}$ = 5 Н;
S = 20 $см^{2}$;
$ρ_{гл} = 1260 кг/м^{3}$;
Найти:
p − ?
СИ:
h = 0,4 м;
S = 0,002 $м^{2}$;
$h_{1} = 0,3$ м;
Решение:
$p_{п}=\frac{P}{S}$;
$p_{п}=\frac{5}{0,002} = 2500$ Па;
$p_{гл} = gρh$;
g ≈10 Н/кг;
$p_{гл} = 10 * 1260 * 0,4 = 5040$ Па;
Если атмосферное давление не учитывать, то давление глицерина на дно сосуда равно:
$p = p_{п} + p_{гл}$;
p = 2500 + 5040 = 7540 Па ≈ 7,5 кПа..
Ответ: 7,5 кПа.
б) Дано:
h = 40 см;
$P_{п}$ = 5 Н;
S = 20 $см^{2}$;
$h_{1} = 30$ см;
$ρ_{гл} = 1260 кг/м^{3}$;
Найти:
$p_{h_{1}}$ − ?
СИ:
h = 0,4 м;
S = 0,002 $м^{2}$;
$h_{1} = 0,3$ м;
Решение:
$p_{п}=\frac{P}{S}$;
$p_{п}=\frac{5}{0,002} = 2500$ Па;
$p_{гл} = gρh$;
g ≈10 Н/кг;
$p_{гл} = 10 * 1260 * 0,3 = 3780$ Па;
Если атмосферное давление не учитывать, то давление глицерина на дно сосуда равно:
$p_{h_{1}} = p_{п} + p_{гл}$;
$p_{h_{1}} = 2500 + 3780 = 6280$ Па ≈ 6,3 кПа.
Ответ: 6,3 кПа.
Задание №349
До какой высоты h следует налить однородную жидкость в сосуд, имеющий форму куба со стороной А, чтобы сила давления жидкости на дно сосуда была равна силе давления жидкости на его боковые стенки?
Решение
Дано:
сторона = А;
$F_{1} = F_{2}$.
Найти:
h − ?
Решение:
$p=\frac{F}{S}$;
Площадь дна равна:
$S_{1} = А^{2}$;
$p_{1} = gρh$;
$F_{1} = p_{1}S_{1} = gρhА^{2}$;
Так как давление в жидкости равномерно возрастает от нуля у поверхности до максимального своего значения у дна, то среднее давление на боковую стенку можно определить, считая высоту равной $\frac{h}{2}$, тогда
$p_{2} = gρ\frac{h}{2}$.
Площадь 4 боковых стенок равна:
$S_{2} = 4Аh$;
Сила давления на 4 стенки будет равна:
$F_{2} = p_{2}S_{2} = gρ\frac{h}{2} * 4Аh = 2gρAh^{2}$;
Если $F_{1} = F_{2}$, то
$gρhА^{2} = 2gρAh^{2}$;
2h = A;
$h = \frac{A}{2}$.
Ответ. Однородную жидкость следует налить до высоты $\frac{A}{2}$.
Задание №350
Под колоколом воздушного насоса находится сосуд, закупоренный пробкой. Почему при интенсивном выкачивании воздуха из−под колокола пробка может вылететь (рис. 28)?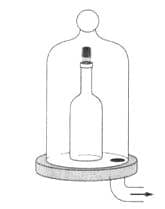 рис. 28
рис. 28
Решение
При откачке воздуха из−под колокола уменьшается число молекул воздуха в единице объема, следовательно, и давление в колоколе. Через некоторое время это давление становится меньше давления в бутылке, и в результате пробка вылетает.
Задание №351
Если пустую бутылку поставить на землю и ударить по горлышку сверху вниз, то разбить бутылку не удастся. Однако, наполнив бутылку водой доверху и закрыв пробкой, достаточно несильно ударить по пробке, как бутылка разбивается на части. Объясните этот необычный способ разбивания бутылок.
Решение
При наличии воды давление в сосуде будет распространяться во все стороны одинаково. Это приведет к разрушению бутылки. При вертикальном ударе по горлышку пустой бутылки давление направлено по направлению действия силы.

