Задание №1685
На проволоке подвешены один над другим три шара массами $m_{1} = 10$ кг, $m_{2} = 8$ кг, $m_{3} = 3$ кг (рис. 262). Определите силу натяжения проволоки между нижним и средним шарами; средним и верхним шарами; верхним шаром и точкой крепления проволоки к опоре.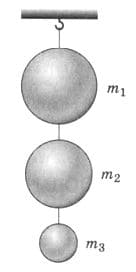 рис. 262
рис. 262
Решение
Дано:
$m_{1} = 10$ кг;
$m_{2} = 8$ кг;
$m_{3} = 3$ кг;
g ≈ 10 Н/кг.
Найти:
$T_{1}$ − ?
$T_{2}$ − ?
$T_{3}$ − ?
Решение: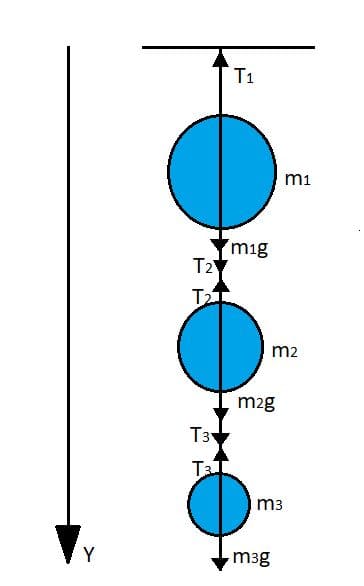 Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$.
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{T}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{T_{2}} + \overset{→}{T_{1}}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{T_{3}} + \overset{→}{T_{2}}$;
$\overset{→}{m_{3}а} = \overset{→}{m_{3}g} + \overset{→}{T_{3}}$;
Выберем ось Y перпендикулярно горизонтальной плоскости. Рассмотрим уравнения в проекции на вертикальную ось:
Ось Y:
$0 = m_{1}g + T_{2} - T_{1}$;
$0 = m_{2}g + T_{3} - T_{2}$;
$0 = m_{3}g - T_{3}$;
$T_{3} = m_{3}g$;
$T_{3} = 3 * 10 = 30$ Н;
$T_{2} = m_{2}g + T_{3}$;
$T_{2} = 8 * 10 + 30 = 110$ Н;
$T_{1} = m_{1}g + T_{2}$;
$T_{1} = 10 * 10 + 110 =210$ Н.
Ответ: 30 Н; 110 Н; 210 Н.
Задание №1686
К двум сцепленным динамометрам (рис. 263) подвешен груз массой m = 2 кг. Масса каждого динамометра 200 г. Каково показание верхнего динамометра; нижнего динамометра? рис. 263
рис. 263
Решение
Дано:
$m_{1} = m_{2} = m = 200$ г;
$m_{3} = 2$ кг;
g = 9,8 Н/кг.
Найти:
$P_{1}$ − ?
$P_{2}$ − ?
СИ:
$m_{1} = m_{2} = m = 0,2$ кг;
Решение:
Каждый динамометр показывает вес груза, привешенного к нему снизу:
$P_{1} = mg + m_{3}g$;
$P_{1} = 0,2 * 10 + 2 * 10 = 22$ Н;
$P_{2} = m_{3}g$;
$P_{2} = 2 * 10 = 20$ Н.
Ответ: 22 Н; 20 Н.
Задание №1687
На рисунке 264 изображены грузы, массы которых $m_{1} = 3$ кг и $m_{2} = 2$ кг. В какую сторону будут двигаться грузы и с каким ускорением? Чему равна сила натяжения шнура? Блок считать невесомым, нить − невесомой и нерастяжимой, трением пренебречь.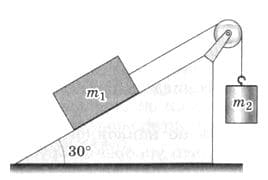 рис. 264
рис. 264
Решение
Дано:
$m_{1} = 3$ кг;
$m_{2} = 2$ кг;
g ≈ 10 Н/кг.
Найти:
a − ?
T − ?
Решение:
Так как нить невесома и нерастяжима, то силы натяжения, действующие на грузы, со стороны нити одинаковы. Ускорения грузов в силу нерастяжимости нити имеют одинаковую величину.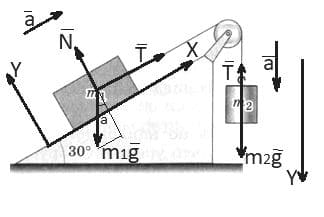 Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила натяжения нити $\overset{→}{T}$.
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила натяжения нити $\overset{→}{T}$.
Запишем второй закон Ньютона в векторной форме для каждого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{N} + \overset{→}{T}$;
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{T}$;
Начертим оси координат для каждого груза.
Рассмотрим уравнения в проекции на ось X:
$m_{1}а = T - m_{1}gsinα$;
Рассмотрим уравнения в проекции на ось Y:
$0 = N - m_{1}gcosα$;
$m_{2}а = m_{2}g - T$;
$\begin{equation*} \begin{cases} m_{1}а = T - m_{1}gsinα &\\ m_{2}а = m_{2}g - T & \end{cases} \end{equation*}$
Сложим уравнения:
$m_{1}а + m_{2}а = m_{2}g - m_{1}gsinα$;
$a * (m_{1} + m_{2}) = m_{2}g - m_{1}gsinα$;
$a = \frac{m_{2}g - m_{1}gsinα}{m_{1} + m_{2}}$;
$a = \frac{2 * 10 - 3 * 10 * 0,5}{3 + 2} = 1 м/с^{2}$;
$T = m_{2}g - m_{2}a = m_{2} * (g - a)$;
T = 2 * (10 − 1) = 18 Н.
Ответ: 1 $м/с^{2}$; 18 Н. Грузы будут двигаться в сторону второго тела.
Задание №1688
На рисунке 265 изображены грузы А и В, имеющие равные массы $m_{1} = m_{2} = 1$ кг. Углы наклона плоскостей к горизонту α = 30°, β = 45°. В какую сторону и с каким ускорением будут двигаться грузы? Чему равна сила натяжения нити? Блок считать невесомым, нить − невесомой и нерастяжимой, силой трения пренебречь.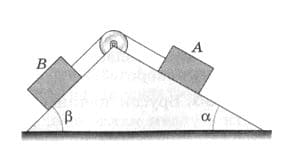 рис. 265
рис. 265
Решение
Дано:
$m_{1} = m_{2} = m = 1$ кг;
α = 30°;
β = 45°;
g ≈ 10 Н/кг.
Найти:
a − ?
T − ?
Решение: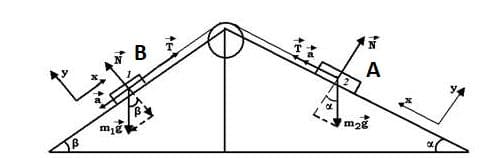 Так как нить невесома и нерастяжима, то силы натяжения, действующие на грузы, со стороны нити одинаковы. Ускорения грузов в силу нерастяжимости нити имеют одинаковую величину.
Так как нить невесома и нерастяжима, то силы натяжения, действующие на грузы, со стороны нити одинаковы. Ускорения грузов в силу нерастяжимости нити имеют одинаковую величину.
Изобразим все силы, действующие на грузы: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила натяжения нити $\overset{→}{T}$.
Начертим оси координат для каждого груза.
Запишем второй закон Ньютона в векторной форме для первого груза:
$\overset{→}{m_{1}а} = \overset{→}{m_{1}g} + \overset{→}{N} + \overset{→}{T}$;
Проекции на оси:
ось X: $-m_{1}а = T - m_{1}gsinβ$;
ось Y: $0 = N - m_{1}gcosβ$;
Сила натяжения нити:
$T = m_{1}gsinβ - m_{1}а =m_{1} * (gsinβ - a)$;
Запишем второй закон Ньютона в векторной форме для второго груза:
$\overset{→}{m_{2}а} = \overset{→}{m_{2}g} + \overset{→}{N} + \overset{→}{T}$;
Проекции на оси:
ось X: $m_{2}а = T - m_{2}gsinα$;
ось Y: $0 = N - m_{2}gcosα$;
Тогда:
$m_{2}а = m_{1}gsinβ - m_{1}а - m_{2}gsinα$;
$m_{1}а + m_{2}а = m_{1}gsinβ - m_{2}gsinα$;
$a * (m_{1} + m_{2}) = m_{1}gsinβ - m_{2}gsinα$;
$a = \frac{m_{1}gsinβ - m_{2}gsinα}{m_{1} + m_{2}} = \frac{gm * (sinβ - sinα)}{2m }$;
$a = \frac{ 10 * 1 * (sin45 - sin30)}{2 * 1} = \frac{ 10 * (0,7 - 0,5)}{2} =1 м/с^{2}$;
$T = 1 * (10 * sin45 - 1) = 6$ Н.
Ответ: 1 $м/с^{2}$; 6 Н. Грузы будут двигаться влево.
Задание №1689
Мальчик вращает в горизонтальной плоскости три связанных верёвкой шара (рис. 266). Расстояние между шарами 1 м, масса каждого шара 0,1 кг. Чему равны силы натяжения всех трёх кусков верёвки, если шар 3 движется со скоростью 6 м/с? Какая из верёвок разорвётся в первую очередь, если вращение ускорить? Силой тяжести шаров пренебречь.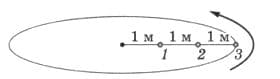 рис. 266
рис. 266
Решение
Дано:
$m_{1} = m_{2} = m = 0,1$ кг;
$l_{1} = l_{2} = l_{3} = l = 1$ м;
$v_{3} = 6$ м/с.
Найти:
$T_{1}$ − ?
$T_{2}$ − ?
$T_{3}$ − ?
Решение: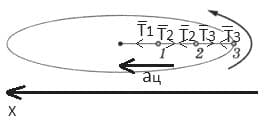 Изобразим силы натяжения нити $\overset{→}{T_{1}}$, $\overset{→}{T_{2}}$, $\overset{→}{T_{3}}$, действующие на шары.
Изобразим силы натяжения нити $\overset{→}{T_{1}}$, $\overset{→}{T_{2}}$, $\overset{→}{T_{3}}$, действующие на шары.
Запишем второй закон Ньютона в векторной форме для каждого шара:
$\overset{→}{mа_{1}} = \overset{→}{T_{1}} + \overset{→}{T_{2}}$;
$\overset{→}{mа_{2}} = \overset{→}{T_{2}} + \overset{→}{T_{3}}$;
$\overset{→}{mа_{3}} = \overset{→}{T_{3}}$;
Выберем ось X параллельно горизонтальной плоскости. Рассмотрим уравнения в проекции на горизонтальную ось:
Ось X:
$mа_{1} = T_{1} - T_{2}$;
$mа_{2} = T_{2} - T_{3}$;
$mа_{3} = T_{3}$;
$a_{ц} = \frac{v^{2}}{R}$;
$T_{3} = \frac{mv_{3}^{2}}{R_{3}}$;
$R_{3} =3 * l = 3 * 1 = 3$ м;
$T_{3} = \frac{0,1 *6^{2}}{3} = 1,2$ Н;
Найдем период обращения 3−го шара.
$T_{3} = \frac{2πR_{3}}{v_{3}}$;
$T_{3} = \frac{2 * 3,14 * 3}{6} = 3,14$ с;
Так шары связаны одной веревкой, то период обращения одинаков для всех трех шаров.
$T_{1} = T_{2} = T_{3}$;
Найдем скорость движения 1−го и 2−го шаров:
$R_{2} = 2 * l = 2 * 1 = 2$ м;
$R_{1} = 1 * l = 1 * 1 = 1$ м;
$v_{2} = \frac{2πR_{2}}{T}$;
$v_{2} = \frac{2 * 3,14 * 2}{3,14} = 4$ м/с;
$v_{2} = \frac{2 * 3,14 * 1}{3,14} = 2$ м/с;
Найдем силу натяжения 2−го куска верёвки:
$T_{2} = mа_{2} + T_{3} = \frac{mv_{2}^{2}}{R_{2}} + T_{3}$;
$T_{2} = \frac{0,1 * 4^{2}}{2} + 1,2 = 2$ Н;
Найдем силу натяжения 1−го куска верёвки:
$T_{1} = mа_{1} + T_{2} = \frac{mv_{1}^{2}}{R_{1}} + T_{2}$;
$T_{1} = \frac{0,1 * 2^{2}}{1} + 2 = 2,4$ Н;
Ответ: 2,4 Н; 2 Н; 1,2 Н. Ели вращение ускорить, разорвётся в первую очередь 1−й кусок веревки, т.к. в нем сила натяжения больше.

