Задание №1446

Зависимость скорости велосипедиста от времени выражается уравнением v = 5 − 0,25t (м/с). Чему равно ускорение велосипедиста? Определите его скорость в момент времени t = 8 с. Через какое время велосипедист остановится?

Решение

Дано:
v = 5 − 0,25t (м/с).
Найти:
a − ?
$v_{8}$ − ?
$t_{v=0}$ − ?
Решение:
Уравнение скорости:
$v = v_{0} + at$;
Из уравнения следует, что a = −0,25 $м/с^{2}$, $v_{0} = 5$ м/с;
$v_{8} = 5 - 0,25 * 8 = 3$ м/с;
$at = v - v_{0}$;
$t = \frac{v - v_{0}}{a}$;
$t_{v=0} = \frac{0 - 5}{-0,25} = 20$ с.
Ответ: −0,25 $м/с^{2}$; 3 м/с; 20 с.

Задание №1447

Уравнение скорости движения тела v = 8 + 2t (м/с). Укажите значения начальной скорости тела и его ускорения. Чему равны перемещение за 10 с движения и скорость в конце десятой секунды?

Решение

Дано:
v = 8 + 2t (м/с).
Найти:
a − ?
$v_{0}$ − ?
$S_{10}$ − ?
$v_{10}$ − ?
Решение:
Уравнение скорости:
$v = v_{0} + at$;
Из уравнения следует, что a = 2 $м/с^{2}$, $v_{0} = 8$ м/с;
$v_{10} = 8 + 2 * 10 = 28$ м/с;
$S = \frac {v_{0} + v_{10}}{2} * t$;
$S = \frac {8 + 28}{2} * 10 = 180$ м.
Ответ: 2 $м/с^{2}$, 8 м/с; 28 м/с; 180 м.

Задание №1448

Уравнение движения тела $х = 4 + 1,5t + t^{2}$ (м). Какое это движение Напишите уравнение скорости движения тела. Чему равны скорость и координата тела через 6 с движения?

Решение

Дано:
$х = 4 + 1,5t + t^{2}$ (м).
Найти:
$v_{t}$ − ?
$v_{6}$ − ?
$x_{6}$ − ?
Решение:
Прямолинейное равноускоренное движение.
Уравнение координаты при равноускоренном прямолинейном движении:
$х = x_{0} + v_{0}t + \frac{at^{2}}{2}$.
Из уравнения следует, что $x_{0} = 4$ м; $v_{0} = 1,5$ м/с; $a = 2 м/с^{2}$;
Уравнение скорости движения:
$v = v_{0} + at$;
Подставим значения из уравнения координаты в уравнение скорости:
$v = 1,5 + 2t$ м/с;
$v_{6} = 1,5 + 2 * 6 = 13,5$ (м/с);
$х_{6} = 4 + 1,5 * 6 + 6^{2} = 49$ м.
Ответ: Прямолинейное равноускоренное движение; $v = 1,5 + 2t$ (м/с); 13,5 м/с; 49 м.

Задание №1449

Какое движение описывают приведённые уравнения х = 6 + 7t (м), $х = 5t^{2}$ (м), $х = 9t - 4t^{2}$ (м), $х= 8t - 6t^{2}$ (м)? Чему равно ускорение для каждого случая?

Решение

Дано:
х = 6 + 7t (м);
$х = 5t^{2}$ (м);
$х = 9t - 4t^{2}$ (м);
$х= 8t - 6t^{2}$ (м).
Найти:
а − ?
Решение:
х = 6 + 7t (м) − прямолинейное равномерное движение.
Уравнение координаты при равномерном прямолинейном движении:
$х = x_{0} + vt$;
Из уравнения следует, что a = 0.
$х = 5t^{2}$ (м) − прямолинейное равноускоренное движение.
Уравнение координаты при равноускоренном прямолинейном движении:
$х = x_{0} + v_{0}t + \frac{at^{2}}{2}$.
Из уравнения следует, что $x_{0} = 0$; $v_{0} = 0$; $a = 10 м/с^{2}$;
$х = 9t - 4t^{2}$ (м) − прямолинейное равнозамедленное движение.
Из уравнения следует, что $x_{0} = 0$; $v_{0} = 9$ м/с; $a = -8 м/с^{2}$;
$х= 8t - 6t^{2}$ (м) − прямолинейное равнозамедленное движение.
Из уравнения следует, что $x_{0} = 0$; $v_{0} = 8$ м/с; $a = -12 м/с^{2}$.
Ответ: равномерное, a = 0; равноускоренное, a = 10 $м/с^{2}$; равнозамедленное, a = − 8 $м/с^{2}$; равнозамедленное, a = − 12 $м/с^{2}$.

Задание №1450

С помощью таблицы постройте график зависимости скорости автомобиля от времени. Определите по графику, с какой скоростью двигался автомобиль в моменты времени 3,5 с; 5,4 с. Какой путь прошёл он за время от $t_{1} = 2$ с до $t_{2} = 5$ с?

Время, с 0 1 2 3 4 5 6
Скорость, м/с 5 8 11 14 17 20 23
Решение
График зависимости скорости автомобиля от времени.
$v = v_{0} + at$;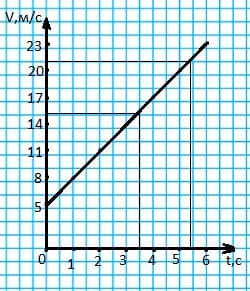
В моменты времени 3,5 с; 5,4 с автомобиль двигался со скоростью 15,5 м/с; 21,2 м/с соответственно.
Найдем ускорение автомобиля:
$at = v - v_{0}$;
$a = \frac{v - v_{0}}{t}$;
Согласно графику $v_{0} = 5$ м/с, $v_{1} = 8$ м/с;
$a = \frac{8-5}{1} = 3 м/с^{2}$.
Найдем путь, который прошёл автомобиль за время от $t_{1} = 2$ с до $t_{2} = 5$ с:
$S = S_{5} - S_{2}$, где $S_{5}$ − путь, пройденный телом за 5 секунд, $S_{2}$ − путь, пройденный телом за 2 секунды.
$S = v_{0}t + \frac {at^{2}}{2}$
$S_{5} = 5 * 5 + \frac {3 * 5^{2}}{2} = 62,5$ м;
$S_{2} = 5 * 2 + \frac {3 * 2^{2}}{2} = 16$ м;
S = 62,5 − 16 = 46,5 м.
Ответ: 15,5 м/с; 21,2 м/с; 46,5 м.

Задание №1451

Постройте графики скорости самолёта при разгоне ($v_{0} = 0, а = 1,5 м/с^{2}$), поезда при движении с места ($v_{0} = 0, а = 0,3 м/с^{2}$).

Решение

Уравнение скорости движения:
$v = v_{0} + at$;
Уравнение скорости для самолета:
v = 1,5t;
График зависимости скорости самолета от времени.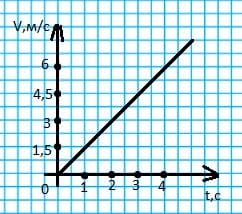
Уравнение скорости для поезда:
v = 0,3t;
График зависимости скорости поезда от времени.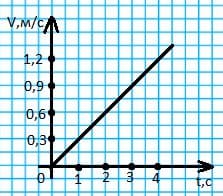

Задание №1452

По графикам, представленным на рисунке 235, определите:
а) характер каждого движения;
б) ускорение;
в) скорость в момент времени t = 2 с;
г) путь, пройденный телами за интервал времени от 0 до 2 с;
д) что означают точки пересечения графиков.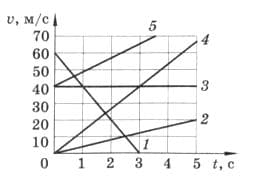
рис. 235

Решение

а) 1 − прямолинейное равнозамедленное движение.
2 − прямолинейное равноускоренное движение.
3 − прямолинейное равномерное движение.
4 − прямолинейное равноускоренное движение.
5 − прямолинейное равноускоренное движение.

б) Найдем ускорение тела:
$v = v_{0} + at$;
$at = v - v_{0}$;
$a = \frac{v - v_{0}}{t}$;
Из 1 графика следует, что $v_{0} = 60$ м/с, v = 0; t = 3 с.
$a_{1} = \frac{0 - 60}{3} = - 20 м/с^{2}$;
Из 2 графика следует, что $v_{0} = 0$, v = 20 м/с; t = 5 с.
$a_{2} = \frac{20 - 0}{5} = 4 м/с^{2}$;
Из 3 графика следует, что a = 0, т.к. скорость тела постоянна.
Из 4 графика следует, что $v_{0} = 0$, v = 65 м/с; t = 5 с.
$a_{4} = \frac{65 - 0}{5} = 13 м/с^{2}$;
Из 5 графика следует, что $v_{0} = 40$ м/с, v = 70 м/с; t = 3,5 с.
$a_{4} = \frac{70 - 40}{3,5} = 8,6 м/с^{2}$.

в) Найдем скорость в момент времени t = 2 с;
$v_{1} = 60 - 20 * 2 = 20$ м/с;
$v_{2} = 4 * 2 = 8$ м/с;
$v_{3} = 40$ м/с;
$v_{4} = 13 * 2 = 26$ м/с;
$v_{5} = 40 + 8,6 * 2 = 57,2$ м/с.

г) $S = v_{0}t + \frac {at^{2}}{2}$;
Путь, пройденный телами за интервал времени от 0 до 2 с, равен:
$S_{1} = 60 * 2 + \frac {-20 * 2^{2}}{2} = 80$ м;
$S_{2} = 0 * 2 + \frac {4 * 2^{2}}{2} = 8$ м;
$S_{3} = vt = 40 * 2 = 80$ м;
$S_{4} = 0 * 2 + \frac {13 * 2^{2}}{2} = 26$ м;
$S_{5} = 40 * 2 + \frac {8,6 * 2^{2}}{2} = 97,2$ м.

д) Точки пересечения графиков − это моменты времени, в которые скорости тел совпадают.