Задание №18
Определите цену деления шкалы каждого из термометров, изображённых на рисунке 3. Какую максимальную и минимальную температуру можно измерить с помощью этих термометров? Какую температуру показывает каждый термометр? Результаты запишите с учётом погрешности измерения.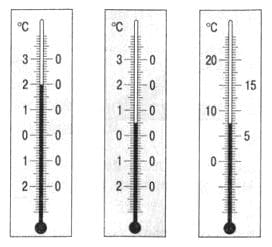
рис. 3
Решение
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
Цена деления термометра слева = $\frac{20-10}{10} = 1$ °C.
$t_{max}$ = 39°C, $t_{min}$ = −30 °C.
Погрешность измерения − 0,5 °C.
t = (20 ± 0,5) °C.
Цена деления термометра посередине = $\frac{20-10}{10} = 1$ °C.
$t_{max}$ = 39°C, $t_{min}$ = −30 °C.
Погрешность измерения − 0,5 °C.
t = (5 ± 0,5) °C.
Цена деления термометра справа = $\frac{20-15}{10} = 0,5$ °C.
$t_{max}$ = 24,5°C, $t_{min}$ = −10 °C.
Погрешность измерения − 0,25 °C.
t = (7,5 ± 0,25) °C.
Задание №19
Переведите значения следующих физических величин в Международную систему единиц (СИ): масса хоккейной шайбы 160 г; масса первого искусственного спутника Земли 0,0836 т; рекордная глубина погружения батискафа в море 10,919 км; диаметр молекулы 0,0003 мм; скорость вращения Земли вокруг Солнца 29,8 км/с.
Решение
СИ:
Масса − кг
Длина − м
Скорость − м/с
Масса хоккейной шайбы: 160 г * 0,001 = 0,16 кг (1 г = 0,001 кг).
Масса первого искусственного спутника Земли: 0,0836 т * 1000 = 83,6 кг (1 т = 1000 кг).
Рекордная глубина погружения батискафа в море: 10,919 км * 1000 = 10919 м (1 км = 1000 м).
Диаметр молекулы: 0,0003 мм = 0,0000003 м = $3 * 10^{-7}$ м (1 мм = 0,001 м).
Скорость вращения Земли вокруг Солнца: 29,8 км/с * 1000 = 29800 м/с (1 км/с = 1000 м/с).
Задание №20
Результат измерения длины шариковой ручки записан в следующем виде: l = (12,00 ± 0,05) см. Чему равны погрешность измерения; цена деления измерительного прибора; истинное значение длины ручки?
Решение
Погрешность измерения = 0,05 см = 0,5 мм.
Цена деления = 0,05 * 2 = 0,1 см = 1 мм.
Истинное значение длины ручки:
11,95 см ⩽ l ⩽ 12,05 см
Задание №21
Результат измерения объёма жидкости в мензурке записан в следующем виде: 79,5 $см^{3}$ ⩽ V ⩽ 80,5 $см^{3}$ . Чему равна цена деления мензурки; погрешность измерения?
Решение
V = (80 ± 0,5) $см^{3}$.
Погрешность измерения = 0,5 $см^{3}$.
Цена деления мензурки = (0,5 * 2) = 1 $см^{3}$.
Задание №22
Спортсмен пробежал дистанцию 100 м за 12,25 с. Чему равна цена деления секундомера; погрешность измерения? Как правильно с учётом погрешности записать истинное значение времени?
Решение
Цена деления секундомера − 0,01 сек.
Погрешность измерения − 0,005 сек.
Истинное значение времени:
12,245 с ⩽ t ⩽ 12,255 с
Задание №23
С помощью рулетки измерьте среднюю длину своего шага. Затем шагами измерьте длину и ширину класса, длину школьного коридора, длину и ширину своей комнаты и выразите их в метрах. Сколько потребуется сделать шагов, чтобы пройти расстояние, равное 60 м; 100 м?
Решение
Допустим длина шага (l) равна 50 см.
Длина класса составляет 16 шагов ($N_{1}$)
Ширина класса − 12 шагов ($N_{2}$).
Длина школьного коридора − 60 шагов ($N_{3}$).
Длина комнаты − 12 шагов ($N_{4}$)
Ширина комнаты − 6 шагов ($N_{5}$)
Длина (S) = l * N;
$S_{1}$ = 50 * 16 = 800 см = 8 м.
$S_{2}$ = 50 * 12 = 600 см = 6 м.
$S_{3}$ = 50 * 60 = 3000 см = 30 м.
$S_{4}$ = 50 * 12 = 600 см = 6 м.
$S_{5}$ = 50 * 6 = 300 см = 3 м.
Чтобы пройти расстояние, равное 60 м, потребуется сделать ($\frac{6000}{50}$) 120 шагов.
Чтобы пройти расстояние, равное 100 м, потребуется сделать ($\frac{10000}{50}$) 200 шагов.
Задание №24
В современном спорте мировые рекорды измеряют с высокой точностью. Результаты спортивных рекордов возьмите из справочников или Интернета и заполните таблицу.
| Вид спорта | Рекорд | Рекорд с учётом погрешности измерения |
| Бег на 100 м, с | ||
| Плавание брасом на 100 м, с | ||
| Прыжок в длину, см | ||
| Прыжок в высоту, см |
Решение
| Вид спорта | Рекорд | Рекорд с учётом погрешности измерения |
| Бег на 100 м, с | 9,58 | (9,58 ± 0,005) с |
| Плавание брасом на 100 м, с | 56,88 | (56,88 ± 0,005) с |
| Прыжок в длину, см | 895 | (895 ± 0,5) см |
| Прыжок в высоту, см | 245 | (245 ± 0,5) см |

