Задание №1738
В каком случае двигатель мотоцикла совершает большую работу − при разгоне с места до скорости 20 км/ч или при увеличении скорости от 20 до 40 км/ч?
Решение
Дано:
$v_{1} = 0$ км/ч;
$v_{2} = 20$ км/ч;
$v_{1}^{'} = 20$ км/ч;
$v_{2}^{'} = 40$ км/ч.
Найти:
$\frac{А'}{A}$ − ?
Решение:
Изменение кинетической энергии тела равно работе всех сил, действующих на тело:
$E_{к2} - E_{к1} = А$;
$A = \frac{mv_{2}^{2}}{2} - \frac{mv_{1}^{2}}{2} = \frac{m}{2} * (v_{2}^{2} - v_{1}^{2})$;
$A' = \frac{m}{2} * (v_{2}'^{2} - v_{1}'^{2})$;
$\frac{А'}{A} = \frac{ \frac{m}{2} * (v_{2}'^{2} - v_{1}'^{2})}{\frac{m}{2} * (v_{2}^{2} - v_{1}^{2})} = \frac{v_{2}'^{2} - v_{1}'^{2}}{v_{2}^{2} - v_{1}^{2}}$;
$\frac{А'}{A} = \frac{40^{2} - 20^{2}}{20^{2} - 0} = \frac{1200}{400} = 3$.
Ответ: Во втором случае в 3 раза большую.
Задание №1739
Тело массой 2 кг, находящееся на высоте 3 м, обладает энергией, равной
80 Дж. Чему равна кинетическая энергия тела на этой высоте; скорость тела?
Решение
Дано:
m = 2 кг;
h = 3 м;
E = 80 Дж.
Найти:
$E_{к}$ − ?
v − ?
Решение:
$E = E_{п} + E_{к}$;
$E_{п} = mgh$;
$E_{к} = E - E_{п} = E - mgh$;
$E_{к} = 80 - 2 * 10 * 3 = 20$ Дж;
$E_{к}= \frac{mv^{2}}{2}$;
$2E_{к}= mv^{2}$;
$v^{2} = \frac{2E_{к}}{m}$;
$v = \sqrt{\frac{2E_{к}}{m}}$;
$v = \sqrt{\frac{2 * 20}{2}} = 4,5$ м/с.
Ответ: 20 Дж; 4,5 м/с.
Задание №1740
Космический корабль «Спейс Шаттл» был пробит куском обшивки массой 200 г при скорости движения 900 км/ч. Какая сила со стороны куска обшивки подействовала на стенку корабля, если принять её толщину равной 10 см?
Решение
Дано:
m = 200 г;
v = 900 км/ч;
d = 10 см.
Найти:
F − ?
СИ:
m = 0,2 кг;
v = 250 м/с;
d = 0,1 м.
Решение:
Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
$А = \frac{mv^{2}}{2} = E_{к}$;
A = Fd;
$Fd = \frac{mv^{2}}{2}$;
$F = \frac{\frac{mv^{2}}{2}}{d} = \frac{mv^{2}}{2d}$;
$F = \frac{0,2 * 250^{2}}{2 * 0,1} = 62500$ Н = 62,5 кН.
Ответ: 62,5 кН.
Задание №1741
Ракета массой 500 кг с помощью ракеты − носителя была поднята на высоту $4*10^{4}$ м и приобрела скорость $1,4 * 10^{3}$ м/с. Рассчитайте полную механическую энергию ракеты.
Решение
Дано:
m = 500 кг;
$h = 4*10^{4}$ м;
$v =1,4 * 10^{3}$ м/с;
g = 10 Н/кг.
Найти:
E − ?
Решение:
$E_{п} = mgh$;
$E_{к}= \frac{mv^{2}}{2}$;
$E= E_{п} + E_{к} = mgh + \frac{mv^{2}}{2}$;
$E= 500 * 10 * 4*10^{4} + \frac{500 * (1,4 * 10^{3})^{2}}{2} = 2 * 10^{8} + 4,9 * 10^{9}= 6,9 * 10^{8}$ Дж = 690 МДж.
Ответ: 690 МДж.
Задание №1742
Тележка начинает двигаться на «американских горках» из точки А с начальной скоростью $v_{0} = 0$ (рис. 271). Чему равна её скорость в обозначенных на рисунке точках? Трением пренебречь.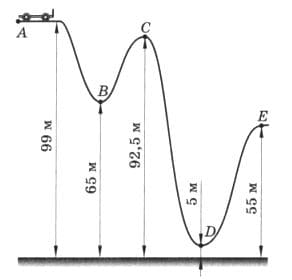 рис. 271
рис. 271
Решение
Дано:
$v_{A} = 0$;
$h_{A} = 99$ м;
$h_{B} = 65$ м;
$h_{C} = 92,5$ м;
$h_{D} = 5$ м;
$h_{E} = 55$ м;
g = 10 Н/кг.
Найти:
$v_{B}$− ?
$v_{C}$− ?
$v_{D}$− ?
$v_{E}$− ?
Решение:
В точке A тележка обладает максимальной потенциальной энергией и нулевой кинетической ($E_{кA} = 0$). Полная механическая энергия тележки равна:
$E = E_{кA} + E_{пA} = mgh_{A} + 0 = mgh_{A}$;
Согласно закону сохранения механической энергии:
$E = E_{пB} + E_{кB} = mgh_{B} + \frac{mv_{B}^{2}}{2}$;
$ \frac{mv_{B}^{2}}{2} = E - mgh_{B} = mgh_{A} - mgh_{B} = mg * (h_{A} - h_{B})$;
$mv_{B}^{2} = 2mg * (h_{A} - h_{B})$;
$v_{B}^{2} = \frac{2mg * (h_{A} - h_{B}}{m}) = 2g * (h_{A} - h_{B}) $;
$v_{B} = \sqrt{2g * (h_{A} - h_{B})}$;
$v_{B} = \sqrt{2 * 10 * (99 - 65)}= 26,1$ м/с;
$v_{С} = \sqrt{2g * (h_{A} - h_{C})}$;
$v_{С} = \sqrt{2 * 10 * (99 - 92,5)}= 11,4$ м/с;
$v_{D} = \sqrt{2g * (h_{A} - h_{D})}$;
$v_{D} = \sqrt{2 * 10 * (99 - 5)}= 43,3$ м/с;
$v_{E} = \sqrt{2g * (h_{A} - h_{E})}$;
$v_{E} = \sqrt{2 * 10 * (99 - 55)}= 29,7$ м/с;
Ответ: 26,1 м/с; 11,4 м/с; 43,3 м/с; 29,7 м/с.
Задание №1743
Ракета взлетает вертикально вверх и достигает высоты 150 м. Определите массу ракеты, если скорость истечения газов равна 217 м/с, считая, что сгорание заряда происходит мгновенно. Масса заряда 50 г.
Решение
Дано:
$v_{2}= 217$ м/с;
h = 150 м;
$m_{2} = 50$ г;
g = 10 Н/кг.
Найти:
$m_{1}$ − ?
СИ:
$m_{2} = 0,05$ г;
Решение:
Согласно закону сохранения импульса:
$m_{1}v_{1} + m_{2}v_{2} = m_{1}v_{1}^{'} + m_{2}v_{2}^{'}$;
Так как в начальной точке, скорость ракеты и топлива была равна нулю, тогда в проекции на ось X, уравнение примет вид:
$0 = m_{1}v_{1}^{'} - m_{2}v_{2}^{'}$;
$m_{1}v_{1}^{'} = m_{2}v_{2}^{'}$;
$m_{1} = \frac{m_{2}v_{2}^{'}}{v_{1}^{'}}$;
Согласно закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
Т.к. в нижней точке потенциальная энергия, а в верхней точке − кинетическая энергия ракеты, равны нулю, уравнение примет вид:
$E_{к1} = E_{п2}$;
$\frac{mv_{1}^{1}}{2} = m_{1}gh$;
$m_{1}v_{1}^{2} = 2m_{1}gh$;
$v_{1}^{2} = \frac{2m_{1}gh}{m_{1}} = 2gh$;
$v_{1} = \sqrt{2gh}$;
$m_{1} = \frac{m_{2}v_{2}^{'}}{\sqrt{2gh}}$;
$m_{1} = \frac{0,05 * 217}{\sqrt{2 * 10 * 150}} = 0,2$ кг = 200 г.
Ответ: 200 г.
Задание №1744
Шар массой 5 кг падает с высоты 2 м и сжимает пружину жёсткостью 500 Н/м (рис. 272). Масса пружины пренебрежимо мала по сравнению с массой шара. Чему равно максимальное сжатие пружины?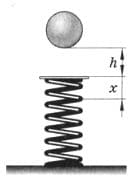 рис. 272
рис. 272
Решение
Дано:
m = 5 кг;
h = 2 м;
k = 500 Н/м;
g = 10 Н/кг.
Найти:
x − ?
Решение:
Система пружина − шар является замкнутой, для неё выполняется закон сохранения полной механической энергии.
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
Кинетическая энергия шара в начальной и конечной точке равна нулю. Потенциальная энергия шарика до падения:
$E_{п1} = mg * (h+x)$;
Потенциальная энергия упруго деформированной пружины:
$E_{п2} = \frac{k(x)^{2}}{2}$;
$E_{п1} = E_{п2}$;
$mg * (h+x) = \frac{kx^{2}}{2}$;
$\frac{kx^{2}}{2} - mgh - mgx = 0$;
$x^{2} - \frac{2mg}{k}x - \frac{2mgh}{k} = 0$;
$x^{2} - \frac{2 * 5 * 10}{500}x - \frac{2 * 5 * 10 * 2}{500} = 0$;
$x^{2} - 0,2x - 0,4 = 0$;
Найдем дискриминант квадратного уравнения:
$D = b^{2} - 4ac = (-0,2)^2 - 4 * 1 * ( - 0,4) = 0,04 + 1,6 = 1,64$;
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
$x_{1} = \frac{0,2 - \sqrt{1,64}}{2 * 1} = -0,54$ − не имеет смысла;
$x_{2} = \frac{0,2 + \sqrt{1,64}}{2 * 1} = 0,74$.
Ответ: 0,74 м.
Задание №1745
При выстреле из винтовки пуля массой 7,9 г вылетает из ствола со скоростью 715 м/с. Определите скорость отдачи и энергию отдачи, если масса винтовки 3,8 кг.
Решение
Дано:
$m_{1} = 7,9$ г;
$v_{1}^{'} = 715$ м/с;
$m_{2} = 3,8$ кг.
Найти:
$v_{2}^{'} $ − ?
СИ:
$m_{2} = 0,0079$ кг;
Решение: Закон сохранения импульса:
Закон сохранения импульса:
$m_{1}v_{1} + m_{2}v_{2} = m_{1}v_{1}^{'} + m_{2}v_{2}^{'} $;
В проекции на ось X:
$0 + 0 = m_{1}v_{1}^{'} - m_{2}v_{2}^{'} $;
$m_{1}v_{1}^{'} = m_{2}v_{2}^{'} $;
$v_{2}^{'} = \frac{m_{1}v_{1}^{'}}{m_{2}}$;
$v_{2}^{'} = \frac{0,0079 * 715}{3,8} = 1,5$ м/с;
Кинетическая энергия отдачи винтовки:
$E_{к}= \frac{mv_{2}^{2}}{2}$;
$E_{к}= \frac{3,8 * 1,5^{2}}{2}= 4,2$ Дж;
Ответ: 1,5 м/с; 4,2 Дж.
Задание №1746
С горы высотой 50 м падает камень. На какой высоте кинетическая энергия камня станет равной его потенциальной энергии?
Решение
Дано:
$h_{1} = 50$ м;
$E_{п2} = E_{к2}$.
Найти:
$h_{2}$ − ?
Решение:
Согласно закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
В начальной точке кинетическая энергия равна нулю, тогда:
$E_{п1} = E_{п2} + E_{к2} = E_{п2} + E_{п2} = 2E_{п2} = 2mgh_{2}$;
$mgh_{1} = 2 mgh_{2}$;
$h_{1} = 2h_{2}$;
$h_{2} = \frac{h_{1}}{2}$;
$h_{2} = \frac{50}{2} = 25$ м;
Ответ: 25 м.

