Задание №643
Чему равна масса тела, если при скорости движения 10 м/с оно обладает кинетической энергией 2,5 кДж?
Решение
Дано:
v = 10 м/с;
$E_{к}$ = 2,5 кДж.
Найти:
m − ?
СИ:
$E_{к}$ = 2500 Дж.
Решение:
$E_{к} = \frac{mv^{2}}{2}$;
$m = √ \frac{2E_{к}}{v^{2}}$
$m = \frac{2 * 2500}{10^{2}} = 50$ кг.
Ответ: 50 кг.
Задание №644
Какая работа должна быть совершена для разгона мотоцикла массой 250 кг из состояния покоя до скорости 108 км/ч?
Решение
Дано:
m = 250 кг;
$v_{0} = 0$ м/с;
$v_{1} = 108$ км/ч.
Найти:
А − ?
СИ:
$v_{1} = 30$ м/с.
Решение:
Работа по увеличению скорости мотоцикла равна изменению его кинетической энергии.
$А = ΔE_{к}$;
$E_{к} = \frac{mv^{2}}{2}$;
$А = \frac{m * (v_{1}^{2} - v_{0}^{2})}{2}$;
$А = \frac{250 * (30^{2} - 0^{2})}{2} = 112500$ Дж = 112,5 кДж.
Ответ: 112,5 кДж.
Задание №645
На рисунке 94 представлено положение четырёх тел. Какое из этих тел имеет наибольшую потенциальную энергию; наименьшую потенциальную энергию? рис. 94
рис. 94
Решение
Дано:
$m_{1} = 10$ кг;
$h_{1} = 1$ м;
$m_{2} = 7$ кг;
$h_{2} = 2$ м;
$m_{3} = 6$ кг;
$h_{3} = 3$ м;
$m_{4} = 4$ кг;
$h_{4} = 4$ м;
Найти:
$E_{max}$ − ?
$E_{min}$ − ?
Решение:
$Е_{п} = gmh$;
g = 9,8 Н/кг;
$Е_{п1} = 9,8 * 10 * 1 = 98$ Дж;
$Е_{п2} = 9,8 * 7 * 2 = 137,2$ Дж;
$Е_{п3} = 9,8 * 6 * 3 = 176,4$ Дж;
$Е_{п4} = 9,8 * 4 * 4 = 156,8$ Дж.
Наибольшая потенциальная энергия у 3−го тела, наименьшая потенциальная энергия у 1−го тела.
Ответ: наибольшая потенциальная энергия у 3−го тела, наименьшая потенциальная энергия у 1−го тела.
Задание №646
На какую высоту надо поднять груз массой 5 кг, чтобы его потенциальная энергия увеличилась на 40 Дж?
Решение
Дано:
m = 5 кг;
$ΔЕ_{п} = 40$ Дж
Найти:
h − ?
Решение:
$Е_{п} = gmh$;
h = $\frac{ΔЕ_{п}}{gm}$
g ≈10 Н/кг;
$h = \frac{40}{10 * 50} = 0,8$ м.
Ответ: 0,8 м.
Задание №647
Тело весом 200 Н подняли на высоту 4,6 м. Какой потенциальной энергией обладает тело? Какую работу может совершить оно при падении?
Решение
Дано:
P = 200 Н;
h = 4,6 м.
Найти:
$Е_{п}$ − ?
A − ?
Решение:
$Е_{п} = gmh = Ph$;
$Е_{п} = 200 * 4,6 = 920$ Дж;
А = Ph;
А = 200 * 4,6 = 920 Дж.
Ответ: 920 Дж; 920 Дж.
Задание №648
Какую работу надо совершить, чтобы пружину жесткостью 500 Н/м:
а) растянуть на 2 см; 4 см;
б) сжать на 2 см; 4 см?
Решение
а) Дано:
k = 500 Н/м;
$x_{1} = 2$ см;
$x_{2} = 4$ см.
Найти:
$А_{1}$ − ?
$А_{2}$ − ?
СИ:
$x_{1} = 0,02$ м;
$x_{2} = 0,04$ м.
Решение:
$A = \frac{k * Δx^{2}}{2}$;
$A_{1} = \frac{500 * 0,02^{2}}{2} = 0,1$ Дж;
$A_{2} = \frac{500 * 0,04^{2}}{2} = 0,4$ Дж.
Ответ: 0,1 Дж; 0,4 Дж.
б) Дано:
k = 500 Н/м;
$x_{1} = 2$ см;
$x_{2} = 4$ см.
Найти:
$А_{1}$ − ?
$А_{2}$ − ?
СИ:
$x_{1} = 0,02$ м;
$x_{2} = 0,04$ м.
Решение:
$A = \frac{k * Δx^{2}}{2}$;
$A_{1} = \frac{500 * 0,02^{2}}{2} = 0,1$ Дж;
$A_{2} = \frac{500 * 0,04^{2}}{2} = 0,4$ Дж.
Ответ: 0,1 Дж; 0,4 Дж.
Задание №649
Рассчитайте работу, совершаемую при сжатии пружины на 5 см, если для сжатия её на 1 см необходимо приложить силу 10 Н.
Решение
Дано:
F = 10 Н;
$Δx_{1} = 1$ см;
$Δx_{2} = 5$ см.
Найти:
$А_{2}$ − ?
СИ:
$Δx_{1} = 0,01$ м;
$Δx_{2} = 0,05$ м.
Решение:
$F_{упр}=k Δx$;
$k = \frac{F_{упр}}{ Δx}$;
$k = \frac{10}{0,01} = 1000$ Н/м;
$A = \frac{k * Δx^{2}}{2}$;
$A_{2} = \frac{1000* 0,05^{2}}{2} = 1,25$ Дж.
Ответ: 1,25 Дж.
Задание №650
Какую работу необходимо совершить, чтобы растянуть недеформированную пружину жёсткостью $10^{3}$ Н/м на 10 см; чтобы растянуть пружину ещё на 10 см?
Решение
Дано:
k = $10^{3}$ Н/м
$Δx_{1} = 10$ см;
$Δx_{2} = 20$ см.
Найти:
$А_{1}$ − ?
$А_{2}$ − ?
СИ:
$Δx_{1} = 0,1$ см;
$Δx_{2} = 0,2$ см.
Решение:
$A = \frac{k * Δx^{2}}{2}$;
$A_{1} = \frac{10^{3} * 0,1^{2}}{2} = 5$ Дж;
$A= \frac{10^{3} * 0,2^{2}}{2} = 20$ Дж;
$А_{2} = A - A_{1} = 20 - 5 = 15$ Дж.
Ответ: 5 Дж; 15 Дж.
Задание №651
Динамометр, рассчитанный на силу 40 Н, имеет пружину жёсткостью 500 Н/м. Какую работу надо совершить, чтобы растянуть пружину от начала шкалы до последнего деления?
Решение
Дано:
F = 40 Н;
k = 500 Н/м.
Найти:
А − ?
Решение:
$F_{упр}=kΔx_{max}$;
$Δx_{max} = \frac{F_{упр}}{k}$;
$Δx_{max} = \frac{40}{500} = 0,08$ м;
$A = \frac{k * Δx^{2}}{2}$;
$A = \frac{500 * 0,08^{2}}{2} = 1,6$ Дж.
Ответ: 1,6 Дж.
Задание №652
По графику зависимости растяжения пружины от приложенной силы (рис. 95) рассчитайте:
а) жёсткость пружины;
б) силу упругости, возникающую при растяжении пружины на 3 см; 5 см;
в) потенциальную энергию пружины, сжатой на 2 см; 5 см.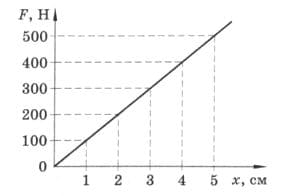 рис. 95
рис. 95
Решение
а) $F_{упр}=kΔх$;
$k = \frac{F_{упр}}{Δх}$;
$k = \frac{500}{0,05} = 10000$ Н/м.
б) Сила упругости, возникающая при растяжении пружины на 3 см − 300 Н.
Сила упругости, возникающая при растяжении пружины на 5 см − 500 Н.
в) $E = \frac{k * Δx^{2}}{2}$;
$E_{1}= \frac{10000 * 0,02^{2}}{2} = 2$ Дж;
$E_{2}= \frac{10000 * 0,05^{2}}{2} = 12,5$ Дж.

