Ответы к стр. 107 . Отрезки, соединяющие вершины многоугольника

Данной темой мы открываем последний тематический блок первой части учебника. В нем будут рассмотрены вопросы геометрического характера. Начинаем мы с рассмотрения такого нового геометрического понятия, как диагональ многоугольника. Понятие диагонали будет в дальнейшем использовано при проведении разбиения многоугольника на треугольники.

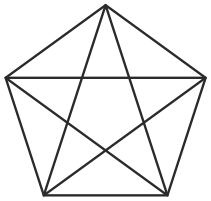
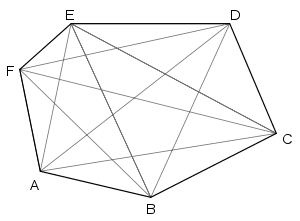
369. Построй пятиугольник. Соедини каждую пару его вершин отрезком.
Обведи те отрезки, которые образуют границу пятиугольника. Как называются эти отрезки? Сколько отрезков осталось необведёнными? Эти отрезки называются диагоналями.
Сторона соединяет соседние вершины многоугольника. Какие вершины соединяет его диагональ?

При выполнении задания 369 учащиеся познакомятся с понятием диагонали многоугольника как отрезка, соединяющего вершины многоугольника, но не входящего в состав границы этого многоугольника, т. е. не являющегося стороной многоугольника. Для примера построения диагоналей многоугольника желательно рассматривать только выпуклые многоугольники, т. е. такие, для которых любая диагональ не выходит за границу этого многоугольника.

370. Сколько сторон и сколько диагоналей у четырёхугольника? У шестиугольника? У треугольника?

При выполнении задания  учащиеся на практике смогут установить зависимость между числом диагоналей и числом сторон рассматриваемого многоугольника.
Так, у четырехугольника две диагонали, у шестиугольника их уже девять, а у треугольника их нет совсем.

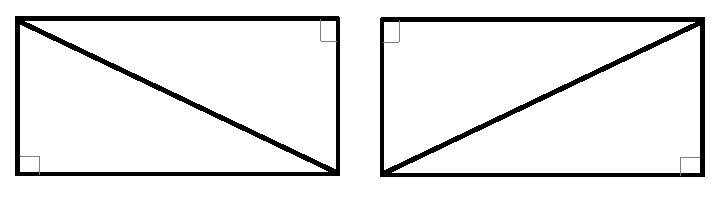
371. На какие два треугольника делит прямоугольник его диагональ? Сделай чертёж.

Диагональ делит прямоугольник на два прямоугольных треугольника.

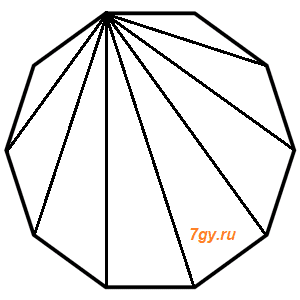
372. Сколько диагоналей выходит из одной вершины десятиугольника? Сделай чертёж.

Для ответа на этот вопрос учащиеся могут воспользоваться соответствующим чертежом, но могут обойтись и без чертежа. Для этого они должны понять, что из данной вершины десятиугольника можно провести диагонали в 7 вершин этого многоугольника, так как нельзя провести диагональ в эту же вершину, а также в две соседние.

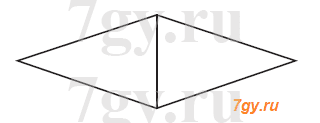
373. Начерти многоугольник, у которого диагональ лежит на оси симметрии. Проведи эту диагональ в построенном многоугольнике.

Задание 373 относится к заданиям повышенной сложности. Для его выполнения учащиеся должны вспомнить понятие «ось симметрии ». Многоугольником, у которого диагональ лежит на оси симметрии, может быть прямоугольник, в том числе квадрат, а может быть и произвольный ромб.

374. Может ли сторона многоугольника быть длиннее диагонали, если они выходят из одной и той же вершины? Проиллюстрируй свой ответ с помощью чертежа.

Задание относится к заданиям повышенной сложности. В нем учащимся предлагается сравнить по длине сторону и диагональ, которые выходят из одной вершины многоугольника. На первый взгляд может показаться, что диагональ всегда длиннее стороны, и примеров тому можно привести достаточно много. На самом деле это не так: диагональ может быть и короче стороны.

375. Начерти многоугольник, у которого ровно 9 диагоналей.

Задание относится к заданиям повышенной сложности. В нем учащимся предлагается начертить многоугольник, у которого ровно 9 диагоналей. В результате выполнения задания 370 учащиеся уже узнали, что у шестиугольника ровно 9 диагоналей. Поэтому начертить учащиеся могут любой выпуклый шестиугольник.