Ответы к стр. 124

11. Предлагается вычислить жилую площадь квартиры, которая складывается из площадей трех комнат. Размеры каждой комнаты можно узнать из данной таблицы. Так как комнаты имеют прямоугольную форму, то для вычисления их площади нужно воспользоваться формулой площади прямоугольника.

12. Для выполнения задания 12 сначала нужно сравнить площадь данного листа бумаги (7•7 = 49 (кв. см)) с общей площадью 50 «единичных» квадратов (1•50 = 50 (кв. см)). Так как общая площадь квадратов больше площади листа бумаги, то вырезать это число квадратов из данного листа бумаги нельзя ни при каком способе разрезания! Квадрат со стороной 2 см имеет площадь 4 кв. см. Поэтому максимальное число таких квадратов, которые можно вырезать из данного листа бумаги, если не учитывать возникающие при выкраивании ограничения, можно определить с помощью деления с остатком: 49 : 4 = 12 (ост. 1), т. е. в лучшем случае таких квадратов можно вырезать 12 штук. На самом деле их будет меньше. Реально удается вырезать только 9 «целых» квадратов (рис. 14). Если разрезать нужным образом оставшиеся полоски, то из их частей можно было бы сложить еще 3 таких квадрата (12 – 9 = 3).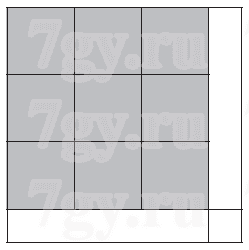

13. Задание относится к заданиям повышенной сложности. Для его выполнения учащиеся сначала должны вычислить площадь листа бумаги прямоугольной формы (20•10 = 200 (кв. см)). После этого они должны вычислить площадь прямоугольного треугольника, предварительно установив, что катеты этого треугольника имеют длину 9 см и 12 см (сторона 15 см не может выступать в роли катета, так как она самая длинная из трех данных сторон). Площадь прямоугольного треугольника они могут вычислить, умножив длину одного катета на половину длины другого (9•6 = 54 (кв. см)). Теперь можно вычислить площадь оставшихся обрезков (200 – 54 = 146 (кв. см)).