Пункт 42. Измерение углов. Транспортир. Страница 148

Задание 802

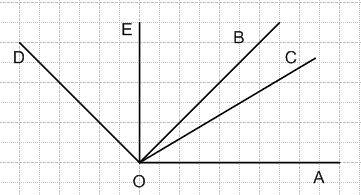
По рисунку 85 определите градусные меры углов:
а) AKD, АКБ, AKF;
б) BKF, ВКЕ, ВКС, BKD;
в) DKC, DKE, DKF, СКЕ, CKF и EKF.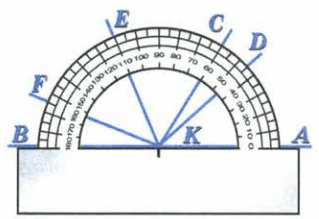

Решение

а) ∠AKD = 45°, ∠AKF = 155°, ∠AKE = 110°.

б) ∠BKF = 25°, ∠BKE = 70°, ∠BKE = 120°, ∠BKD = 135°.

в) ∠DKC = 60° − 45° = 15°, ∠DKE = 110° − 45° = 65°, ∠DKF = 155° − 45° = 110°, ∠CKE = 110° − 60° = 50°, ∠CKF = 155°− 60° = 95°, ∠EKF = 155° − 110° = 45°.

Задание 803

Начертите луч ОА. С помощью транспортира по одну сторону от луча ОА постройте:
∠AOB = 45°, ∠AOC = 30°, ∠AOD = 135°, ∠AOE = 90°.

Решение

∠AOC = 30°, ∠AOB = 45°, ∠AOE = 90°, ∠AOD = 135°.

Задание 804

Измерьте углы, изображённые на рисунке 86, и запишите результаты измерений.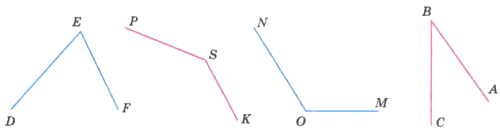

Решение

LDEF = 75°, ∠PSK = 135°, ∠NOM = 112°, ∠ABC = 50°.

Задание 805

Луч ОС лежит внутри угла АОВ, причём ∠AOC = 37°, ∠BOC = 19°. Чему равен угол АОВ?

Решение

∠AOB = ∠АОС + ∠BOC = 37° + 19° = 56°.

Задание 806

Какую часть развёрнутого угла составляют углы в 30°; 45°; 60°?
Какую долю прямого угла составляют углы в 30°; 15°; 60°; 75°?

Решение

30 ° = 30 : 180 = 1/6
45 ° = 45 : 180 = 1/4
60 ° = 60 : 180 = 1/3

30 ° = 30 : 90 = 1/3
15 ° = 15 : 90 = 1/6
60 ° = 60 : 90 = 2/3
75 ° = 75 : 90 = 5/6

Задание 807

Сколько градусов содержит угол, если он составляет:
а) 1/2 развёрнутого угла;
б) 1/3 развёрнутого угла;
в) 5/6 прямого угла;
г) 3/5 прямого угла;
д) 0,1 прямого угла;
е) 0,2 развёрнутого угла?

Решение

а) 1/2 * 180 ° = 180 ° : 2 = 90 °

6) 1/3 * 180 ° = 180 ° : 3 = 60 °

в) 5/6 * 90 ° = 90 ° : 6 * 5 = 75 °

г) 3/5 * 90 ° = 90 ° * 3 : 5 = 54 °

д) 0,1 * 90° = 9°

e) 0,2 * 180° = 36°