Ответы к странице 221

879. Выполните действия и результат представьте в стандартном виде:
1) $1,3 * 10^4 + 1,8 * 10^5$;
2) $1,5 * 10^2 - 2,8 * 10^{-2}$;
3) $5,6 * 10^3 - 3,2 * 10^2$;
4) $4,8 * 10^{-3} + 6 * 10^{-4}$.

Решение:

1) $1,3 * 10^4 + 1,8 * 10^5 = 1,3 * 10^4 + 1,8 * 10^4 * 10 = 10^4(1,3 + 1,8 * 10) = 10^4(1,3 + 18) = 19,3 * 10^4 = 1,93 * 10^5$

2) $1,5 * 10^2 - 2,8 * 10^{-2} = 1,5 * 10^2 - 2,8 * 10^2 * 10^{-4} = 10^2(1,5 - 2,8 * 10^{-4}) = 10^2(1,5 - 0,00028) = 1,49972 * 10^2$

3) $5,6 * 10^3 - 3,2 * 10^2 = 5,6 * 10^2 * 10 - 3,2 * 10^2 = 10^2(5,6 * 10 - 3,2) = 10^2(56 - 3,2) = 52,8 * 10^2 = 5,28 * 10^3$

4) $4,8 * 10^{-3} + 6 * 10^{-4} = 4,8 * 10^{-3} + 6 * 10^{-3} * 10^{-1} = 10^{-3}(4,8 + 6 * 10^{-1}) = 10^{-3}(4,8 + 0,6) = 5,4 * 10^{-3}$

880. Сократите дробь (n − целое число):
1) $\frac{9^{n - 1}}{3^{2n - 3}}$;
2) $\frac{7^{n + 1} * 2^{n - 1}}{14^n}$;
3) $\frac{2^{2n - 1} * 3^{n + 1}}{12^n}$;
4) $\frac{a^6 + a^{11}}{a^{-4} + a}$;
5) $\frac{a^{-3} + a^{-2} + a^{-1}}{a^3 + a^2 + a}$;
6) $\frac{6^{n + 2} - 6^n}{35}$;
7) $\frac{5^{n + 2} - 5^{n - 2}}{5^n}$;
8) $\frac{2^{-n} + 1}{2^n + 1}$.

Решение:

1) $\frac{9^{n - 1}}{3^{2n - 3}} = \frac{(3^2)^{n - 1}}{3^{2n - 3}} = \frac{3^{2n - 2}}{3^{2n - 3}} = 3^{2n - 2 - (2n - 3)} = 3^{2n - 2 - 2n + 3} = 3^{1} = 3$

2) $\frac{7^{n + 1} * 2^{n - 1}}{14^n} = \frac{7^{n + 1} * 2^{n - 1}}{7^n * 2^n} = 7 * 2^{-1} = \frac{7}{2} = 3\frac{1}{2}$

3) $\frac{2^{2n - 1} * 3^{n + 1}}{12^n} = \frac{2^{2n - 1} * 3^{n + 1}}{4^n * 3^n} = \frac{2^{2n - 1} * 3^{n + 1}}{(2^2)^n * 3^n} = \frac{2^{2n - 1} * 3^{n + 1}}{2^{2n} * 3^n} = 2^{-1} * 3 = \frac{3}{2} = 1\frac{1}{2}$

4) $\frac{a^6 + a^{11}}{a^{-4} + a} = \frac{a^6(1 + a^{5})}{a^{-4}(1 + a^5)} = a^{6 - (-4)} = a^{6 + 4} = a^{10}$

5) $\frac{a^{-3} + a^{-2} + a^{-1}}{a^3 + a^2 + a} = \frac{a^{-3}(1 + a + a^2)}{a(a^2 + a + 1)} = a^{-3 - 1} = a^{-4} = \frac{1}{a^4}$

6) $\frac{6^{n + 2} - 6^n}{35} = \frac{6^{n}(6^2 - 1)}{35} = \frac{6^{n}(36 - 1)}{35} = \frac{6^{n} * 35}{35} = 6^{n}$

7) $\frac{5^{n + 2} - 5^{n - 2}}{5^n} = \frac{5^n(5^{2} - 5^{-2})}{5^n} = 25 - \frac{1}{25} = 24\frac{24}{25}$

8) $\frac{2^{-n} + 1}{2^n + 1} = \frac{2^{-n}(1 + 2^n)}{2^n + 1} = 2^{-n} = \frac{1}{2^n}$

881. Функция задана формулой $y = -\frac{24}{x}$. Найдите:
1) значение функции, если значение аргумента равно: −4; 8; 1,2;
2) значение аргумента, при котором значение функции равно: 24; −18; 60.

Решение:

1) $y = -\frac{24}{x}$
при x = −4:
$y = -\frac{24}{-4} = 6$
при x = 8:
$y = -\frac{24}{8} = -3$
при x = 1,2:
$y = -\frac{24}{1,2} = -\frac{240}{12} = -20$

2) $y = -\frac{24}{x}$
при y = 24:
$-\frac{24}{x} = 24$
$x = -\frac{24}{24}$
x = −1
при y = −18:
$-\frac{24}{x} = -18$
$x = -\frac{24}{-18}$
$x = \frac{4}{3}$
$x = 1\frac{1}{3}$
при y = 60:
$-\frac{24}{x} = 60$
$x = -\frac{24}{60}$
$x = -\frac{2}{5}$

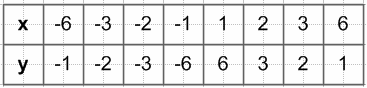
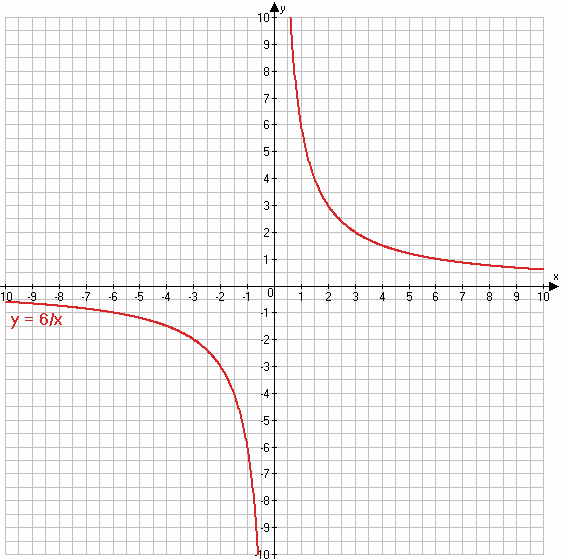
882. Постройте график функции $y = \frac{6}{x}$. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно: 2; −1,5; 4;
2) значение аргумента, при котором значение функции равно: −2; 3; −4,5;
3) значение аргумента, при которых функция принимает отрицательные значения.

Решение:

$y = \frac{6}{x}$


1)
при x = 2: y = 3;
при x = −1,5: y = −4;
при x = 4: y = 1,5.
2)
при y = −2: x = −3;
при y = 3: x = 2;
при y = −4,5: x = −1,5.
3)
Функция принимает отрицательные значения при x < 0.

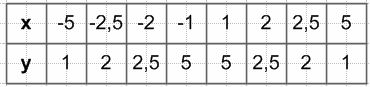
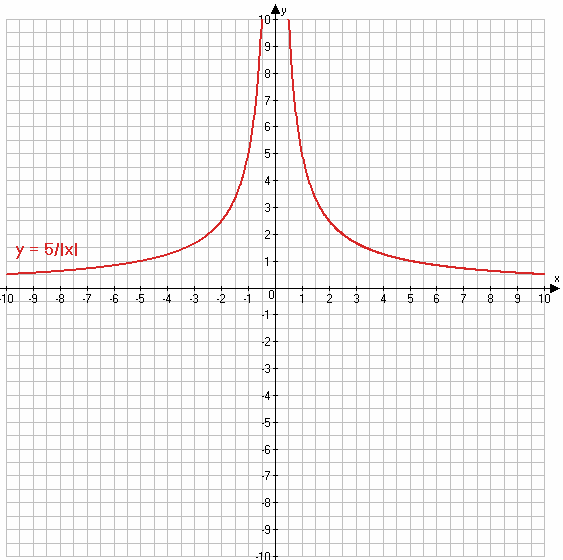
883. Постройте график функции $y = \frac{5}{|x|}$.

Решение:

$y = \frac{5}{|x|}$
если x > 0, то $y = \frac{5}{x}$;
если x < 0, то $y = \frac{5}{-x} = -\frac{5}{x}$

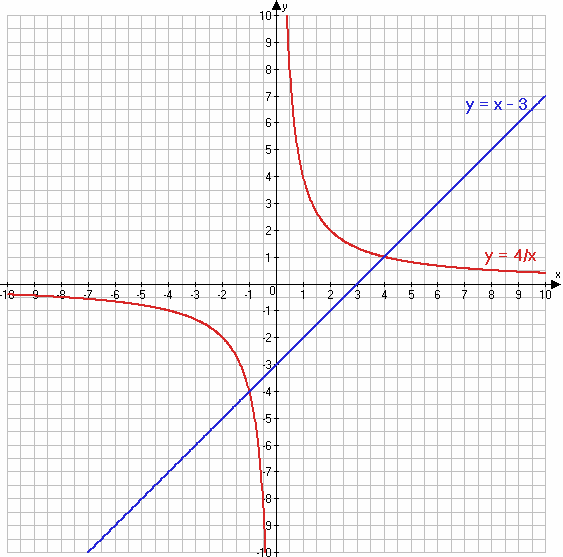
884. Постройте в одной системе координат графики функций $y = \frac{4}{x}$ и y = x − 3 и укажите координаты точек их пересечения.

Решение:

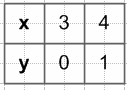
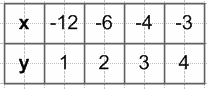
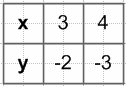
$y = \frac{4}{x}$

y = x − 3

885. Найдите значение p, если известно, что график функции $y = \frac{p}{x}$ проходит через точку:
1) A(−3; 2);
2) $B(-\frac{1}{7}; 3)$;
3) C(−0,4; 1,6).

Решение:

1) $y = \frac{p}{x}$
A(−3; 2)
$2 = \frac{p}{-3}$
p = −3 * 2
p = −6

2) $y = \frac{p}{x}$
$B(-\frac{1}{7}; 3)$
$3 = \frac{-\frac{1}{7}}{x}$
$x = -\frac{1}{7} * 3$
$x = -\frac{3}{7}$

3) $y = \frac{p}{x}$
C(−0,4; 1,6)
$1,6 = \frac{p}{-0,4}$
p = −0,4 * 1,6
p = −0,64

886. Постройте график функции:
1)
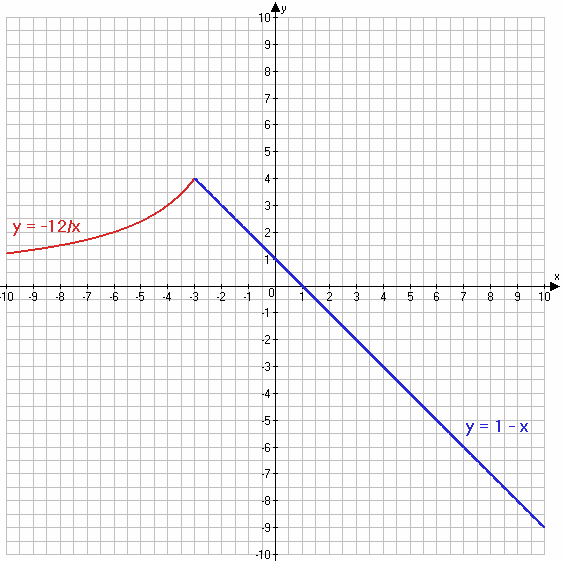
$y = \begin{equation*} \begin{cases} -\frac{12}{x}, если\;x ≤ -3 &\\ 1 - x, если\;x > - 3 & \end{cases} \end{equation*}$
2)
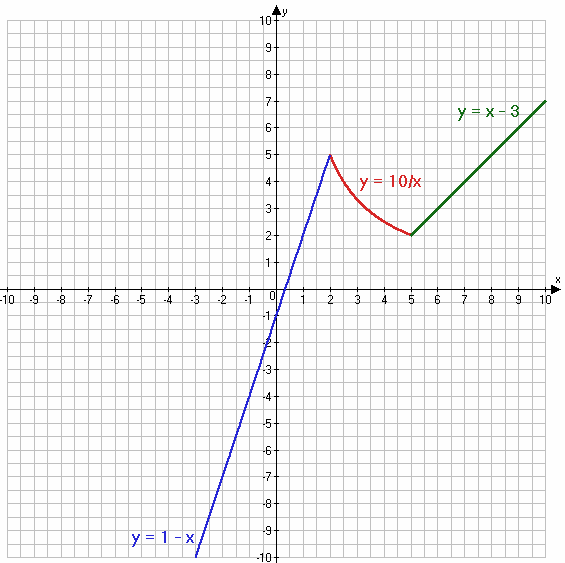
$y = \begin{equation*} \begin{cases} 3x - 1, если\;x < 2 &\\ \frac{10}{x}, если\;2 ≤ x < 5 &\\ x - 3, если\;x ≥ 5 & \end{cases} \end{equation*}$

Решение:

1) $y = \begin{equation*} \begin{cases} -\frac{12}{x}, если\;x ≤ -3 &\\ 1 - x, если\;x > - 3 & \end{cases} \end{equation*}$
$-\frac{12}{x}$ если x ≤ −3

1 − x, если x > − 3



2) $y = \begin{equation*} \begin{cases} 3x - 1, если\;x < 2 &\\ \frac{10}{x}, если\;2 ≤ x < 5 &\\ x - 3, если\;x ≥ 5 & \end{cases} \end{equation*}$
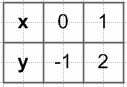
y = 3x − 1, если x < 2

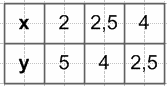
$y = \frac{10}{x}$, если 2 ≤ x < 5

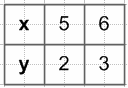
y = x − 3, если x ≥ 5