Ответы к странице 93

361. Постройте график функции:
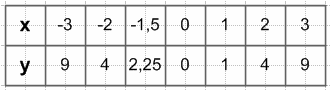
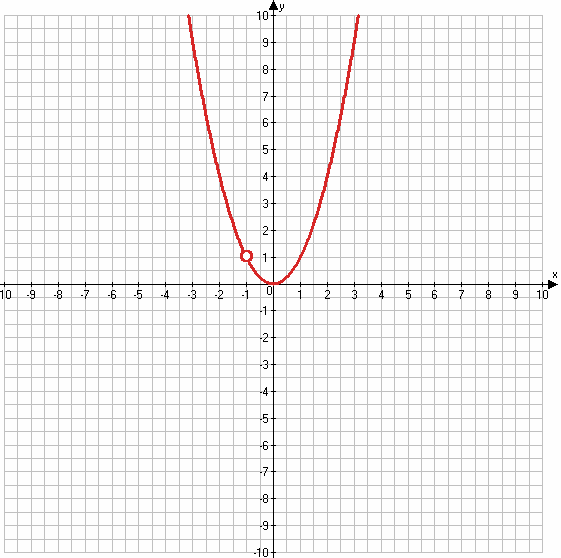
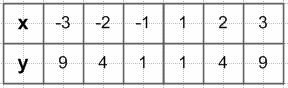
1) $y = \frac{x^3 + x^2}{x + 1}$;
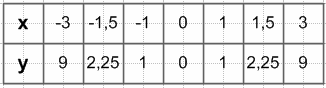
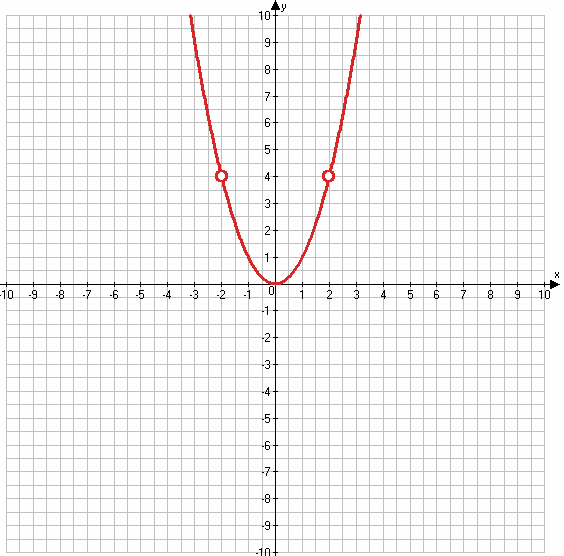
2) $y = \frac{x^4 - 4x^2}{x^2 - 4}$.

Решение:

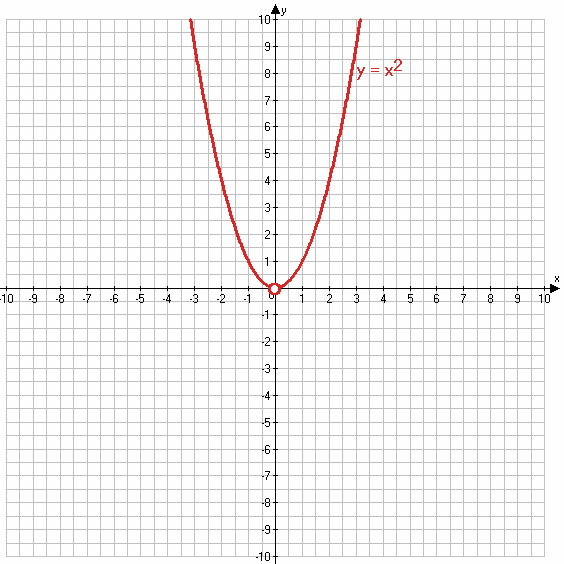
1) $y = \frac{x^3 + x^2}{x + 1} = \frac{x^2(x + 1)}{x + 1} = x^2$
x + 1 ≠ 0
x ≠ −1



2) $y = \frac{x^4 - 4x^2}{x^2 - 4} = \frac{x^2(x^2 - 4)}{x^2 - 4} = x^2$
$x^2 - 4 ≠ 0$
$x^2 ≠ 4$
x ≠ ±2

362. Постройте график функции $y = \frac{x^3}{x}$.

Решение:

$y = \frac{x^3}{x} = x^2$
x ≠ 0

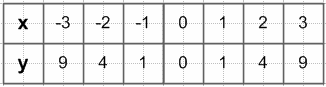
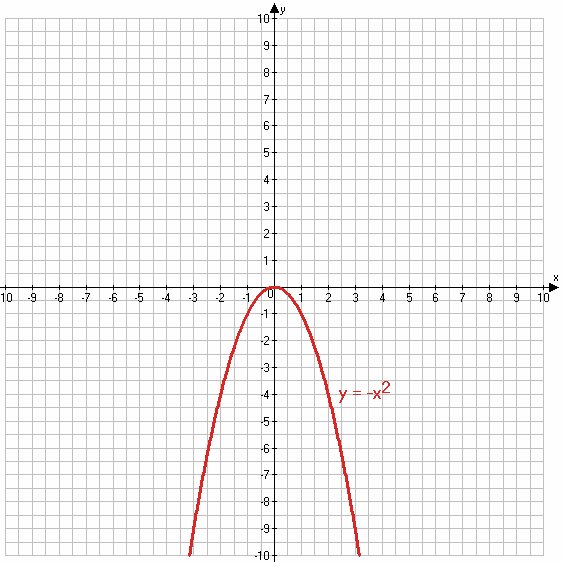
363. Найдите область определения, область значений и нули функции $y = -x^2$. Постройте график этой функции.

Решение:

$y = -x^2$
Область определения функции: все числа.
Область значений функции: все неположительные числа.
y = 0 при x = 0
x = 0 − нуль функции

364. Постройте график уравнения:
1) $\frac{y - x^2}{(x - 1)^2 + (y - 1)^2} = 0$;
2) $\frac{y - x^2}{y - x} = 0$.

Решение:

1) $\frac{y - x^2}{(x - 1)^2 + (y - 1)^2} = 0$
$(x - 1)^2 ≥ 0$
$(y - 1)^2 ≥ 0$
тогда $(x - 1)^2 + (y - 1)^2$ может быть равно нулю, только если $(x - 1)^2 = 0$ и $(y - 1)^2 = 0$, значит:
$(x - 1)^2 ≠ 0$
x − 1 ≠ 0
x ≠ 1
$(y - 1)^2 ≠ 0$
y − 1 ≠ 0
y ≠ 1
Следовательно, точка с координатами (1;1) не принадлежит графику.

$y - x^2 = 0$
$y = x^2$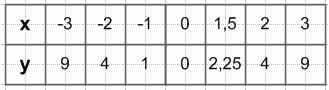



2) $\frac{y - x^2}{y - x} = 0$
y ≠ x

$y - x^2 = 0$
$y = x^2$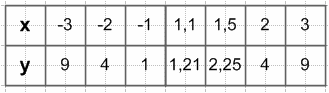

365. Постройте график уравнения:
$\frac{x^2 - y}{(x + 2)^2 + (y - 4)^2 = 0}$

Решение:

$\frac{x^2 - y}{(x + 2)^2 + (y - 4)^2 = 0}$
$(x + 2)^2 ≥ 0$
$(y - 4)^2 ≥ 0$
тогда $(x + 2)^2 + (y - 4)^2$ может быть равно нулю, только если $(x + 2)^2 = 0$ и $(y - 4)^2 = 0$, значит:
$(x + 2)^2 ≠ 0$
x + 2 ≠ 0
x ≠ −2
$(y - 4)^2 ≠ 0$
y − 4 ≠ 0
y ≠ 4
Следовательно, точка с координатами (−2;4) не принадлежит графику.

$y - x^2 = 0$
$y = x^2$

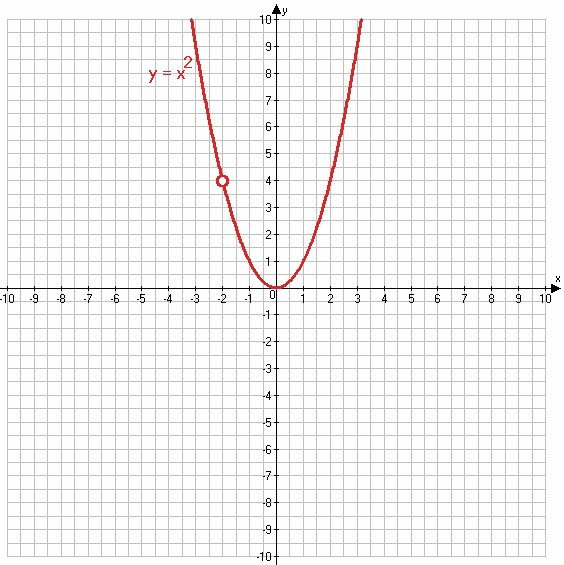
366. Задайте с помощью формул функцию, график которой изображен на рисунке 15.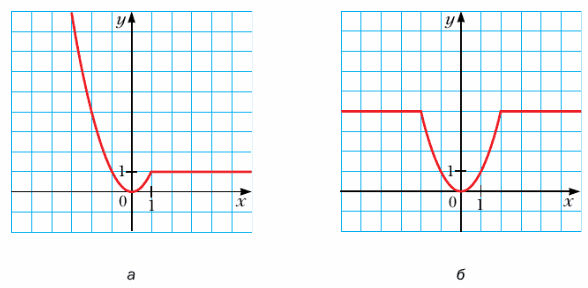

Решение:

а) $y = \begin{equation*} \begin{cases} x^2, при\;x ≤ 1 &\\ 1, при\;x > 1 & \end{cases} \end{equation*}$

б) $y = \begin{equation*} \begin{cases} 4, при\;x ≤ -2 &\\ x^2, при\;-2 < x ≤ 2 &\\ 4, при\;x > 2 & \end{cases} \end{equation*}$

367. Задайте с помощью формул функцию, график которой изображен на рисунке 16.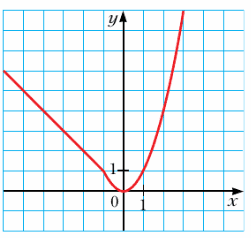

Решение:

$y = \begin{equation*} \begin{cases} -x, при\;x ≤ -1 &\\ x^2, при\;x > -1 & \end{cases} \end{equation*}$