Ответы к странице 222
887. Постройте график функции:
1) $y = \frac{4x + 12}{x^2 + 3x}$;
2) $y = \frac{32 - 2x^2}{x^3 - 16x}$.
Решение:
1) $y = \frac{4x + 12}{x^2 + 3x}$
$x^2 + 3x ≠ 0$
x(x + 3) ≠ 0
x ≠ 0
и
x + 3 ≠ 0
x ≠ −3
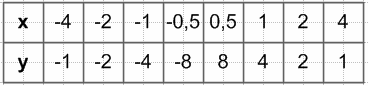
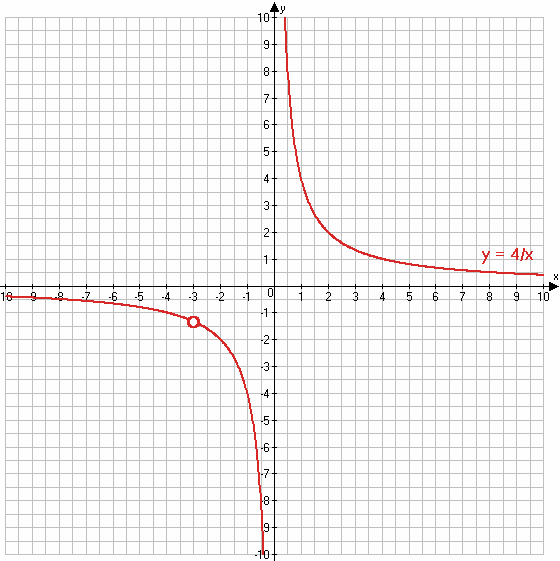
$y = \frac{4x + 12}{x^2 + 3x} = \frac{4(x + 3)}{x(x + 3)} = \frac{4}{x}$
$y = \frac{4}{x}$
2) $y = \frac{32 - 2x^2}{x^3 - 16x}$
$x^3 - 16x ≠ 0$
$x(x^2 - 16) ≠ 0$
x ≠ 0
и
$x^2 - 16 ≠ 0$
$x^2 ≠ 16$
x ≠ ±4
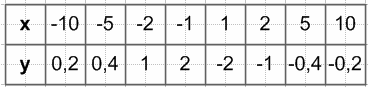
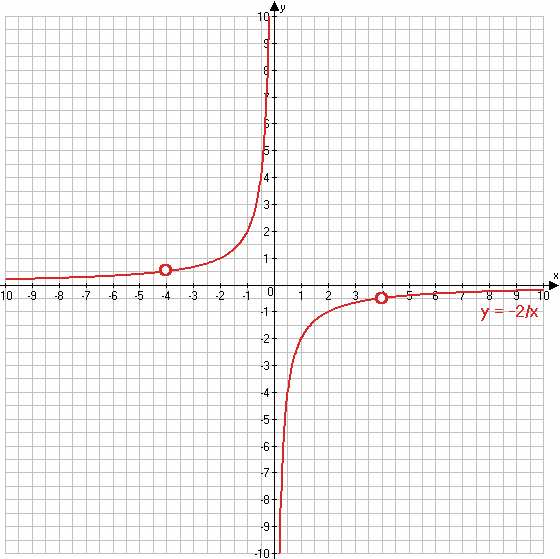
$y = \frac{32 - 2x^2}{x^3 - 16x} = \frac{2(16 - x^2)}{x(x^2 - 16)} = -\frac{2(x^2 - 16)}{x(x^2 - 16)} = -\frac{2}{x}$
$y = -\frac{2}{x}$
888. Найдите значение выражение:
1) $0,4\sqrt{625} - \frac{1}{4}\sqrt{144}$;
2) $\sqrt{64} * \sqrt{0,25} + \sqrt{2^4 + 9}$;
3) $3\sqrt{0,25} - \sqrt{7^2 + 24^2}$;
4) $\sqrt{1\frac{11}{25}} + \sqrt{3\frac{6}{25}} - 0,04\sqrt{10000}$;
5) $\frac{1}{5}\sqrt{625} - \frac{3}{17}\sqrt{289}$.
Решение:
1) $0,4\sqrt{625} - \frac{1}{4}\sqrt{144} = 0,4 * 25 - \frac{1}{4} * 12 = 10 - 3 = 7$
2) $\sqrt{64} * \sqrt{0,25} + \sqrt{2^4 + 9} = 8 * 0,5 + \sqrt{16 + 9} = 4 + \sqrt{25} = 4 + 5 = 9$
3) $3\sqrt{0,25} - \sqrt{7^2 + 24^2} = 3 * 0,5 - \sqrt{49 + 576} = 1,5 - \sqrt{625} = 1,5 - 25 = -23,5$
4) $\sqrt{1\frac{11}{25}} + \sqrt{3\frac{6}{25}} - 0,04\sqrt{10000} = \sqrt{\frac{36}{25}} + \sqrt{\frac{81}{25}} - 0,04 * 100 = \frac{6}{5} + \frac{9}{5} - 4 = \frac{15}{5} - 4 = 3 - 4 = -1$
5) $\frac{1}{5}\sqrt{625} - \frac{3}{17}\sqrt{289} = \frac{1}{5} * 25 - \frac{3}{17} * 17 = 5 - 3 = 2$
889. Найдите значение выражения:
1) $(\sqrt{3})^2 - \sqrt{1,69}$;
2) $(3\sqrt{15})^2 - (15\sqrt{3})^2$;
3) $50 * (-\frac{1}{5}\sqrt{7})^2 - \frac{1}{4} * (3\sqrt{2})^2$;
4) $\sqrt{1089} - (\frac{1}{6}\sqrt{216})^2$;
5) $\frac{4}{9}\sqrt{39,69} - \frac{5}{49}\sqrt{59,29} + (-\frac{1}{5}\sqrt{75})^2$;
6) $\frac{1}{2}\sqrt{17^2 - 15^2} + (2\sqrt{5\frac{1}{2}})^2 - 0,3\sqrt{900}$.
Решение:
1) $(\sqrt{3})^2 - \sqrt{1,69} = 3 - 1,3 = 1,7$
2) $(3\sqrt{15})^2 - (15\sqrt{3})^2 = 9 * 15 - 225 * 3 = 135 - 675 = -540$
3) $50 * (-\frac{1}{5}\sqrt{7})^2 - \frac{1}{4} * (3\sqrt{2})^2 = 50 * \frac{1}{25} * 7 - \frac{1}{4} * 9 * 2 = 2 * 7 - \frac{9}{2} = 14 - 4,5 = 9,5$
4) $\sqrt{1089} - (\frac{1}{6}\sqrt{216})^2 = 33 - \frac{1}{36} * 216 = 33 - 6 = 27$
5) $\frac{4}{9}\sqrt{39,69} - \frac{5}{49}\sqrt{59,29} + (-\frac{1}{5}\sqrt{75})^2 = \frac{4}{9} * 6,3 - \frac{5}{49} * 7,7 + \frac{1}{25} * 75 = 4 * 0,7 - \frac{5}{7} * 1,1 + 3 = 5,8 - \frac{55}{70} = 5\frac{8}{10} - \frac{55}{70} = 5\frac{56}{70} - \frac{55}{70} = 5\frac{1}{70}$
6) $\frac{1}{2}\sqrt{17^2 - 15^2} + (2\sqrt{5\frac{1}{2}})^2 - 0,3\sqrt{900} = \frac{1}{2}\sqrt{(17 - 15)(17 + 15)} + (2\sqrt{\frac{11}{2}})^2 - 0,3 * 30 = \frac{1}{2}\sqrt{2 * 32} + 4 * \frac{11}{2} - 9 = \frac{1}{2}\sqrt{64} + 2 * 11 - 9 = \frac{1}{2} * 8 + 22 - 9 = 4 + 13 = 17$
890. Решите уравнение:
1) $\sqrt{x} = 2$;
2) $\sqrt{x} = \frac{1}{4}$;
3) $\sqrt{x} - 3 = 0$;
4) $2\sqrt{x} - 7 = 0$;
5) $\sqrt{x} + 5 = 0$;
6) $\frac{1}{4}\sqrt{x} + 5 = 0$;
7) $\sqrt{7x} - 4 = 0$;
8) $\sqrt{7x - 4} = 0$;
9) $\sqrt{7x - 4} = 2$;
10) $\frac{28}{\sqrt{x}} = 7$;
11) $\frac{15}{\sqrt{x + 4}} = 3$;
12) $\sqrt{4 + \sqrt{3 + x}} = 5$.
Решение:
1) $\sqrt{x} = 2$
$(\sqrt{x})^2 = 2^2$
x = 4
Ответ: 4
2) $\sqrt{x} = \frac{1}{4}$
$(\sqrt{x})^2 = (\frac{1}{4})^2$
$x = \frac{1}{16}$
Ответ: $\frac{1}{16}$
3) $\sqrt{x} - 3 = 0$
$\sqrt{x} = 3$
$(\sqrt{x})^2 = 3^2$
x = 9
Ответ: 9
4) $2\sqrt{x} - 7 = 0$
$2\sqrt{x} = 7$
$(2\sqrt{x})^2 = 7^2$
4x = 49
$x = \frac{49}{4}$
$x = 12\frac{1}{4}$
5) $\sqrt{x} + 5 = 0$
$\sqrt{x} = -5$
Ответ: нет корней
6) $\frac{1}{4}\sqrt{x} + 5 = 0$
$\frac{1}{4}\sqrt{x} = -5$
$\sqrt{x} = -5 * 4$
$\sqrt{x} = -20$
Ответ: нет корней
7) $\sqrt{7x} - 4 = 0$
$\sqrt{7x} = 4$
$(\sqrt{7x})^2 = 4^2$
7x = 16
$x = \frac{16}{7}$
$x = 2\frac{2}{7}$
Ответ: $2\frac{2}{7}$
8) $\sqrt{7x - 4} = 0$
$(\sqrt{7x - 4})^2 = 0^2$
7x − 4 = 0
7x = 4
$x = \frac{4}{7}$
Ответ: $\frac{4}{7}$
9) $\sqrt{7x - 4} = 2$
$(\sqrt{7x - 4})^2 = 2^2$
7x − 4 = 4
7x = 4 + 4
7x = 8
$x = \frac{8}{7}$
$x = 1\frac{1}{7}$
Ответ: $1\frac{1}{7}$
10) $\frac{28}{\sqrt{x}} = 7$
$\sqrt{x} = \frac{28}{7}$
$\sqrt{x} = 4$
$(\sqrt{x})^2 = 4^2$
x = 16
Ответ: 16
11) $\frac{15}{\sqrt{x + 4}} = 3$
$\sqrt{x + 4} = \frac{15}{3}$
$\sqrt{x + 4} = 5$
$(\sqrt{x + 4})^2 = 5^2$
x + 4 = 25
x = 25 − 4
x = 21
Ответ: 21
12) $\sqrt{4 + \sqrt{3 + x}} = 5$
$(\sqrt{4 + \sqrt{3 + x}})^2 = 5^2$
$4 + \sqrt{3 + x} = 25$
$\sqrt{3 + x} = 25 - 4$
$\sqrt{3 + x} = 21$
$(\sqrt{3 + x})^2 = 21^2$
3 + x = 441
x = 441 − 3
x = 438
Ответ: 438
891. Найдите значение корня:
1) $\sqrt{9 * 100}$;
2) $\sqrt{0,49 * 16}$;
3) $\sqrt{676 * 0,04}$;
4) $\sqrt{0,64 * 0,25 * 121}$;
5) $\sqrt{\frac{25}{196}}$;
6) $\sqrt{18\frac{1}{16}}$;
7) $\sqrt{\frac{9}{64} * \frac{1024}{1089}}$;
8) $\sqrt{3\frac{13}{36} * 4\frac{29}{49}}$.
Решение:
1) $\sqrt{9 * 100} = \sqrt{9} * \sqrt{100} = 3 * 10 = 30$
2) $\sqrt{0,49 * 16} = \sqrt{0,49} * \sqrt{16} = 0,7 * 4 = 2,8$
3) $\sqrt{676 * 0,04} = \sqrt{676} * \sqrt{0,04} = 26 * 0,2 = 5,2$
4) $\sqrt{0,64 * 0,25 * 121} = \sqrt{0,64} * \sqrt{0,25} * \sqrt{121} = 0,8 * 0,5 * 11 = 0,4 * 11 = 4,4$
5) $\sqrt{\frac{25}{196}} = \frac{\sqrt{25}}{\sqrt{196}} = \frac{5}{14}$
6) $\sqrt{18\frac{1}{16}} = \sqrt{\frac{289}{16}} = \frac{\sqrt{289}}{\sqrt{16}} = \frac{17}{4} = 4\frac{1}{4}$
7) $\sqrt{\frac{9}{64} * \frac{1024}{1089}} = \frac{\sqrt{9}}{\sqrt{64}} * \frac{\sqrt{1024}}{\sqrt{1089}} = \frac{3}{8} * \frac{32}{33} = \frac{4}{11}$
8) $\sqrt{3\frac{13}{36} * 4\frac{29}{49}} = \sqrt{\frac{121}{36} * \frac{225}{49}} = \frac{\sqrt{121}}{\sqrt{36}} * \frac{\sqrt{225}}{\sqrt{49}} = \frac{11}{6} * \frac{15}{7} = \frac{11}{2} * \frac{5}{7} = \frac{55}{14} = 3\frac{13}{14}$
892. Найдите значение корня:
1) $\sqrt{75 * 234}$;
2) $\sqrt{2 * 800}$;
3) $\sqrt{1,6 * 12,1}$;
4) $\sqrt{2890 * 2,5}$.
Решение:
1) $\sqrt{75 * 234} = \sqrt{3 * 25 * 3 * 78} = \sqrt{9 * 25 * 78} = \sqrt{9} * \sqrt{25} * \sqrt{78} = 3 * 5\sqrt{78} = 15\sqrt{78}$
2) $\sqrt{2 * 800} = \sqrt{2 * 8 * 100} = \sqrt{16 * 100} = \sqrt{16} * \sqrt{100} = 4 * 10 = 40$
3) $\sqrt{1,6 * 12,1} = \sqrt{16 * 121 * 0,01} = \sqrt{16} * \sqrt{121} * \sqrt{0,01} = 4 * 11 * 0,1 = 44 * 0,1 = 4,4$
4) $\sqrt{2890 * 2,5} = \sqrt{289 * 25} = \sqrt{289} * \sqrt{25} = 17 * 5 = 85$
893. Найдите значение выражения:
1) $\sqrt{108} * \sqrt{3}$;
2) $\sqrt{52} * \sqrt{13}$;
3) $\sqrt{160} * \sqrt{250}$;
4) $\sqrt{0,4} * \sqrt{4,9}$;
5) $\frac{\sqrt{288}}{\sqrt{2}}$;
6) $\frac{\sqrt{90}}{\sqrt{0,225}}$.
Решение:
1) $\sqrt{108} * \sqrt{3} = \sqrt{108 * 3} = \sqrt{36 * 3 * 3} = \sqrt{36} * \sqrt{3^2} = 6 * 3 = 1$
2) $\sqrt{52} * \sqrt{13} = \sqrt{52 * 13} = \sqrt{4 * 13 * 13} = \sqrt{4} * \sqrt{13^2} = 2 * 13 = 26$
3) $\sqrt{160} * \sqrt{250} = \sqrt{160 * 250} = \sqrt{16 * 10 * 25 * 10} = \sqrt{16} * \sqrt{25} * \sqrt{10^2} = 4 * 5 * 10 = 20 * 10 = 200$
4) $\sqrt{0,4} * \sqrt{4,9} = \sqrt{0,4 * 4,9} = \sqrt{4 * 49 * 0,01} = \sqrt{4} * \sqrt{49} * \sqrt{0,01} = 2 * 7 * 0,1 = 14 * 0,1 = 1,4$
5) $\frac{\sqrt{288}}{\sqrt{2}} = \sqrt{\frac{288}{2}} = \sqrt{144} = 12$
6) $\frac{\sqrt{90}}{\sqrt{0,225}} = \sqrt{\frac{90}{0,225}} = \sqrt{\frac{9}{0,0225}} = \frac{\sqrt{9}}{\sqrt{0,0225}} = \frac{3}{0,15} = \frac{300}{15} = 20$