Ответы к странице 225

907. Освободитесь от иррациональности в знаменателе дроби:
1) $\frac{1}{\sqrt{6} + \sqrt{2} + 1}$;
2) $\frac{2}{\sqrt{10} + \sqrt{5} - \sqrt{3}}$.

Решение:

1) $\frac{1}{\sqrt{6} + \sqrt{2} + 1} = \frac{\sqrt{6} + \sqrt{2} - 1}{(\sqrt{6} + \sqrt{2} + 1)(\sqrt{6} + \sqrt{2} - 1)} = \frac{\sqrt{6} + \sqrt{2} - 1}{(\sqrt{6} + \sqrt{2})^2 - 1^2} = \frac{\sqrt{6} + \sqrt{2} - 1}{6 + 2\sqrt{12} + 2 - 1} = \frac{\sqrt{6} + \sqrt{2} - 1}{7 + 2\sqrt{12}} = \frac{(\sqrt{6} + \sqrt{2} - 1)(7 - 2\sqrt{12})}{(7 + 2\sqrt{12})(7 - 2\sqrt{12})} = \frac{\sqrt{6} + \sqrt{2} - 1}{7 + 2\sqrt{12}} = \frac{(\sqrt{6} + \sqrt{2} - 1)(7 - 2\sqrt{12})}{7^2 - (2\sqrt{12})^2} = \frac{7\sqrt{6} + 7\sqrt{2} - 7 - 2\sqrt{72} - 2\sqrt{24} + 2\sqrt{12}}{7^2 - (2\sqrt{12})^2} = \frac{7\sqrt{6} + 7\sqrt{2} - 7 - 2\sqrt{36 * 2} - 2\sqrt{4 * 6} + 2\sqrt{4 * 3}}{49 - 4 * 12} = \frac{7\sqrt{6} + 7\sqrt{2} - 7 - 12\sqrt{2} - 4\sqrt{6} + 4\sqrt{3}}{49 - 48} = 3\sqrt{6} - 5\sqrt{2} + 4\sqrt{3} - 7$

2) $\frac{2}{\sqrt{10} + \sqrt{5} - \sqrt{3}} = \frac{2(\sqrt{10} + \sqrt{5} + \sqrt{3})}{(\sqrt{10} + \sqrt{5} - \sqrt{3})(\sqrt{10} + \sqrt{5} + \sqrt{3})} = \frac{2(\sqrt{10} + \sqrt{5} + \sqrt{3})}{(\sqrt{10} + \sqrt{5})^2 - (\sqrt{3})^2} = \frac{2(\sqrt{10} + \sqrt{5} + \sqrt{3})}{10 + 2\sqrt{50} + 5 - 3} = \frac{2(\sqrt{10} + \sqrt{5} + \sqrt{3})}{12 + 2\sqrt{25 * 2}} = \frac{2(\sqrt{10} + \sqrt{5} + \sqrt{3})}{12 + 10\sqrt{2}} = \frac{2(\sqrt{10} + \sqrt{5} + \sqrt{3})}{2(6 + 5\sqrt{2})} = \frac{(\sqrt{10} + \sqrt{5} + \sqrt{3})(6 - 5\sqrt{2})}{(6 + 5\sqrt{2})(6 - 5\sqrt{2})} = \frac{6\sqrt{10} + 6\sqrt{5} + 6\sqrt{3} - 5\sqrt{20} - 5\sqrt{10} - 5\sqrt{6}}{6^2 - (5\sqrt{2})^2} = \frac{6\sqrt{10} + 6\sqrt{5} + 6\sqrt{3} - 5\sqrt{4 * 5} - 5\sqrt{10} - 5\sqrt{6}}{36 - 25 * 2} = \frac{6\sqrt{10} + 6\sqrt{5} + 6\sqrt{3} - 10\sqrt{5} - 5\sqrt{10} - 5\sqrt{6}}{36 - 50} = \frac{\sqrt{10} - 4\sqrt{5} + 6\sqrt{3} - 5\sqrt{6}}{-14} = -\frac{\sqrt{10} - 4\sqrt{5} + 6\sqrt{3} - 5\sqrt{6}}{14}$

908. Найдите значение выражения:
1) $\frac{5}{4 - 3\sqrt{2}} - \frac{5}{4 + 3\sqrt{2}}$;
2) $\frac{1}{\sqrt{4 + \sqrt{15}} + 1} - \frac{1}{\sqrt{4 + \sqrt{15}} - 1}$;
3) $(\sqrt{5 - 2\sqrt{6}} + \sqrt{5 + 2\sqrt{6}})^2$.

Решение:

1) $\frac{5}{4 - 3\sqrt{2}} - \frac{5}{4 + 3\sqrt{2}} = \frac{5(4 + 3\sqrt{2}) - 5(4 - 3\sqrt{2})}{(4 - 3\sqrt{2})(4 + 3\sqrt{2})} = \frac{20 + 15\sqrt{2} - 20 + 15\sqrt{2}}{4^2 - (3\sqrt{2})^2} = \frac{30\sqrt{2}}{16 - 9 * 2} = \frac{30\sqrt{2}}{16 - 18} = \frac{30\sqrt{2}}{-2} = -15\sqrt{2}$

2) $\frac{1}{\sqrt{4 + \sqrt{15}} + 1} - \frac{1}{\sqrt{4 + \sqrt{15}} - 1} = \frac{\sqrt{4 + \sqrt{15}} - 1 - (\sqrt{4 + \sqrt{15}} + 1)}{(\sqrt{4 + \sqrt{15}} + 1)(\sqrt{4 + \sqrt{15}} - 1)} = \frac{\sqrt{4 + \sqrt{15}} - 1 - \sqrt{4 + \sqrt{15}} - 1}{(\sqrt{4 + \sqrt{15}})^2 - 1^2} = \frac{-2}{4 + \sqrt{15} - 1} = \frac{-2}{3 + \sqrt{15}} = \frac{-2(3 - \sqrt{15})}{(3 + \sqrt{15})(3 - \sqrt{15})} = \frac{-2(3 - \sqrt{15})}{3^2 - (\sqrt{15})^2} = \frac{-2(3 - \sqrt{15})}{9 - (\sqrt{15})^2} = \frac{-2(3 - \sqrt{15})}{9 - 15} = \frac{-2(3 - \sqrt{15})}{-6} = \frac{3 - \sqrt{15}}{3}$

3) $(\sqrt{5 - 2\sqrt{6}} + \sqrt{5 + 2\sqrt{6}})^2 = (\sqrt{5 - 2\sqrt{6}})^2 + 2 * \sqrt{5 - 2\sqrt{6}} * \sqrt{5 + 2\sqrt{6}} + (\sqrt{5 + 2\sqrt{6}})^2 = 5 - 2\sqrt{6} + 2(5^2 - (2\sqrt{6})^2) + 5 + 2\sqrt{6} = 10 + 2(25 - 4 * 6) = 10 + 2(25 - 24) = 10 + 2 * 1 = 12$

909. Упростите выражение:
1) $\frac{\sqrt{x}}{\sqrt{x} - 3} - \frac{x}{x - 9}$;
2) $(\frac{\sqrt{b}}{\sqrt{b} - \sqrt{c}} + \frac{\sqrt{b}}{\sqrt{c}}) : \frac{\sqrt{b}}{\sqrt{b} - \sqrt{c}}$.

Решение:

1) $\frac{\sqrt{x}}{\sqrt{x} - 3} - \frac{x}{x - 9} = \frac{\sqrt{x}}{\sqrt{x} - 3} - \frac{x}{(\sqrt{x} - 3)(\sqrt{x} + 3)} = \frac{\sqrt{x}(\sqrt{x} + 3) - x}{(\sqrt{x} - 3)(\sqrt{x} + 3)} = \frac{x + 3\sqrt{x} - x}{x - 9} = \frac{3\sqrt{x}}{x - 9}$

2) $(\frac{\sqrt{b}}{\sqrt{b} - \sqrt{c}} + \frac{\sqrt{b}}{\sqrt{c}}) : \frac{\sqrt{b}}{\sqrt{b} - \sqrt{c}} = \frac{\sqrt{b} * \sqrt{c} + \sqrt{b}(\sqrt{b} - \sqrt{c})}{\sqrt{c}(\sqrt{b} - \sqrt{c})} * \frac{\sqrt{b} - \sqrt{c}}{\sqrt{b}} = \frac{\sqrt{bc} + b - \sqrt{bc}}{\sqrt{c}} * \frac{1}{\sqrt{b}} = \frac{b}{\sqrt{bc}} = \frac{\sqrt{b}}{\sqrt{c}} = \sqrt{\frac{b}{c}}$

910. Упростите выражение:
1) $\sqrt{(\sqrt{x} + 5)^2 - 20\sqrt{x}} + \sqrt{(\sqrt{x} - 4)^2 + 16\sqrt{x}}$;
2) $\sqrt{a + 2\sqrt{a + 3} + 4} + \sqrt{a - 2\sqrt{a + 3} + 4}$.

Решение:

1) $\sqrt{(\sqrt{x} + 5)^2 - 20\sqrt{x}} + \sqrt{(\sqrt{x} - 4)^2 + 16\sqrt{x}} = \sqrt{x + 10\sqrt{x} + 25 - 20\sqrt{x}} + \sqrt{x - 8\sqrt{x} + 16 + 16\sqrt{x}} = \sqrt{x - 10\sqrt{x} + 25} + \sqrt{x + 8\sqrt{x} + 16} = \sqrt{(\sqrt{x} - 5)^2} + \sqrt{(\sqrt{x} + 4)^2} = |\sqrt{x} - 5| + |\sqrt{x} + 4|$
1)
если $\sqrt{x} - 5 ≥ 0$, то и $\sqrt{x} + 4 > 0$, тогда:
$|\sqrt{x} - 5| + |\sqrt{x} + 4| = \sqrt{x} - 5 + \sqrt{x} + 4 = 2\sqrt{x} - 1$
2)
если $\sqrt{x} - 5 < 0$ и $\sqrt{x} + 4 > 0$, тогда:
$|\sqrt{x} - 5| + |\sqrt{x} + 4| = -(\sqrt{x} - 5) + \sqrt{x} + 4 = -\sqrt{x} + 5 + \sqrt{x} + 4 = 9$
3)
если $\sqrt{x} - 5 < 0$ и $\sqrt{x} + 4 < 0$, тогда:
$|\sqrt{x} - 5| + |\sqrt{x} + 4| = -(\sqrt{x} - 5) - (\sqrt{x} + 4) = -\sqrt{x} + 5 - \sqrt{x} - 4 = -2\sqrt{x} + 1$

2) $\sqrt{a + 2\sqrt{a + 3} + 4} + \sqrt{a - 2\sqrt{a + 3} + 4} = \sqrt{a + 3 + 2\sqrt{a + 3} + 1} + \sqrt{a + 3 - 2\sqrt{a + 3} + 1} = \sqrt{(\sqrt{a + 3})^2 + 2\sqrt{a + 3} + 1} + \sqrt{(\sqrt{a + 3})^2 - 2\sqrt{a + 3} + 1} = \sqrt{(\sqrt{a + 3} + 1)^2} + \sqrt{(\sqrt{a + 3} - 1)^2} = \sqrt{a + 3} + 1 + |\sqrt{a + 3} - 1|$
a + 3 ≥ 0
a ≥ −3
1)
если $\sqrt{a + 3} - 1 ≥ 0$, то:
$\sqrt{a + 3} ≥ 1$
a + 3 ≥ 1
a ≥ 1 − 3
a ≥ −2, значит:
−3 ≤ a ≤ −2
$\sqrt{a + 3} + 1 + |\sqrt{a + 3} - 1| = \sqrt{a + 3} + 1 - \sqrt{a + 3} - 1 = 2$
2)
если a > −2:
$\sqrt{a + 3} + 1 + |\sqrt{a + 3} - 1| = \sqrt{a + 3} + 1 + \sqrt{a + 3} - 1 = 2\sqrt{a + 3}$

911. Упростите выражение:
$\frac{1}{\sqrt{5} + \sqrt{2}} + \frac{1}{\sqrt{8} + \sqrt{5}} + \frac{1}{\sqrt{11} + \sqrt{8}} + ... + \frac{1}{\sqrt{50} + \sqrt{47}}$.

Решение:

$\frac{1}{\sqrt{5} + \sqrt{2}} + \frac{1}{\sqrt{8} + \sqrt{5}} + \frac{1}{\sqrt{11} + \sqrt{8}} + ... + \frac{1}{\sqrt{50} + \sqrt{47}} = \frac{\sqrt{5} - \sqrt{2}}{(\sqrt{5} + \sqrt{2})(\sqrt{5} - \sqrt{2})} + \frac{\sqrt{8} - \sqrt{5}}{(\sqrt{8} + \sqrt{5})(\sqrt{8} - \sqrt{5})} + \frac{\sqrt{11} - \sqrt{8}}{(\sqrt{11} + \sqrt{8})(\sqrt{11} - \sqrt{8})} + ... + \frac{\sqrt{50} - \sqrt{47}}{(\sqrt{50} + \sqrt{47})(\sqrt{50} - \sqrt{47})} = \frac{\sqrt{5} - \sqrt{2}}{5 - 2} + \frac{\sqrt{8} - \sqrt{5}}{8 - 5} + \frac{\sqrt{11} - \sqrt{8}}{11 - 8} + ... + \frac{\sqrt{50} - \sqrt{47}}{50 - 47} = \frac{\sqrt{5} - \sqrt{2}}{3} + \frac{\sqrt{8} - \sqrt{5}}{3} + \frac{\sqrt{11} - \sqrt{8}}{3} + ... + \frac{\sqrt{50} - \sqrt{47}}{3} = \frac{\sqrt{5} - \sqrt{2} + \sqrt{8} - \sqrt{5} + \sqrt{11} - \sqrt{8} + ... + \sqrt{50} - \sqrt{47}}{3} = \frac{-\sqrt{2} + \sqrt{50}}{3} = \frac{\sqrt{50} - \sqrt{2}}{3} = \frac{\sqrt{25 * 2} - \sqrt{2}}{3} = \frac{5\sqrt{2} - \sqrt{2}}{3} = \frac{4\sqrt{2}}{3}$

912. Докажите, что:
$\sqrt{2 + \sqrt{3}} * \sqrt{2 + \sqrt{2 + \sqrt{3}}} * \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{3}}}} * \sqrt{2 - \sqrt{2 + \sqrt{2 + \sqrt{3}}}} = 1$.

Решение:

$\sqrt{2 + \sqrt{3}} * \sqrt{2 + \sqrt{2 + \sqrt{3}}} * \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{3}}}} * \sqrt{2 - \sqrt{2 + \sqrt{2 + \sqrt{3}}}} = \sqrt{2 + \sqrt{3}} * \sqrt{2 + \sqrt{2 + \sqrt{3}}} * \sqrt{2^2 - (\sqrt{2 + \sqrt{2 + \sqrt{3}}})^2} = \sqrt{2 + \sqrt{3}} * \sqrt{2 + \sqrt{2 + \sqrt{3}}} * \sqrt{4 - (2 + \sqrt{2 + \sqrt{3}})} = \sqrt{2 + \sqrt{3}} * \sqrt{2 + \sqrt{2 + \sqrt{3}}} * \sqrt{4 - 2 - \sqrt{2 + \sqrt{3}}} = \sqrt{2 + \sqrt{3}} * \sqrt{2 + \sqrt{2 + \sqrt{3}}} * \sqrt{2 - \sqrt{2 + \sqrt{3}}} = \sqrt{2 + \sqrt{3}} * \sqrt{(2 + \sqrt{2 + \sqrt{3}})(2 - \sqrt{2 + \sqrt{3}})} = \sqrt{2 + \sqrt{3}} * \sqrt{2^2 - (2 + \sqrt{3})} = \sqrt{2 + \sqrt{3}} * \sqrt{4 - 2 - \sqrt{3}} = \sqrt{2 + \sqrt{3}} * \sqrt{2 - \sqrt{3}} = \sqrt{(2 + \sqrt{3})(2 - \sqrt{3})} = \sqrt{2^2 - (\sqrt{3})^2} = \sqrt{4 - 3} = \sqrt{1} = 1$

913. Расположите в порядке возрастания числа: $13; \sqrt{165}; 12,7; \sqrt{171}; 13,4.$

Решение:

$13 = \sqrt{169}$
$12,7 = \sqrt{161,29}$
$13,4 = \sqrt{179,56}$
$\sqrt{161,29} < \sqrt{165} < \sqrt{169} < \sqrt{171} < \sqrt{179,56}$, тогда:
$12,7 < \sqrt{165} < 13 < \sqrt{171} < 13,4$

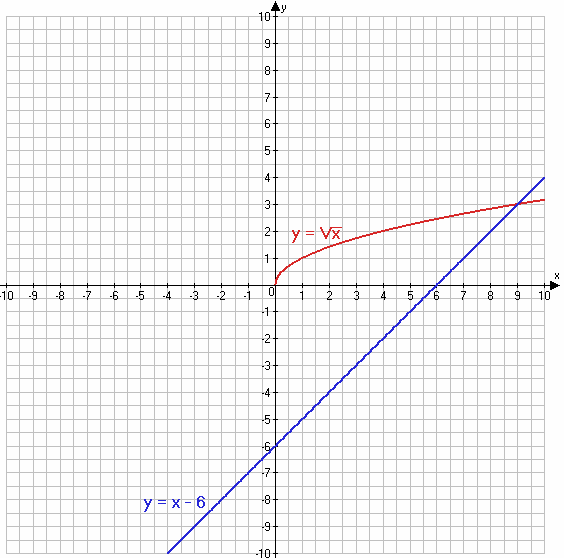
914. Постройте в одной системе координат графики функций $y = \sqrt{x}$ и y = x − 6 и определите координаты точки их пересечения.

Решение:

$y = \sqrt{x}$
х 0 1 4 9
у 0 1 2 3
y = x − 6
х 6 7
у 0 1

Ответ: (9;3) − точка пересечения

915. Между какими двумя последовательными целыми числами находится на координатной прямой число:
1) $\sqrt{67}$;
2) $\sqrt{103}$;
3) $-\sqrt{51,25}$?

Решение:

1) $\sqrt{64} < \sqrt{67} < \sqrt{81}$
$8 < \sqrt{67} < 9$

2) $\sqrt{100} < \sqrt{103} < \sqrt{121}$
$10 < \sqrt{103} < 11$

3) $-\sqrt{64} < -\sqrt{51,25} < -\sqrt{49}$
$-8 < -\sqrt{51,25} < -7$

916. Какие целые числа расположены на координатной прямой между числами:
1) 6 и $\sqrt{67}$;
2) $\sqrt{14}$ и $\sqrt{52}$;
3) $-\sqrt{53}$ и −4,9;
4) $-\sqrt{31}$ и 2,7?

Решение:

1) $6 = \sqrt{36}$
$\sqrt{36} < \sqrt{49} < \sqrt{64} < \sqrt{67}$
$6 < 7 < 8 < \sqrt{67}$
Ответ: 7 и 8

2) $\sqrt{14} < \sqrt{16} < \sqrt{25} < \sqrt{36} < \sqrt{49} < \sqrt{52}$
$\sqrt{14} < 4 < 5 < 6 < 7 < \sqrt{52}$
Ответ: 4; 5; 6; 7.

3) $-4,9 = -\sqrt{24,01}$
$-\sqrt{53} < -\sqrt{49} < -\sqrt{36} < -\sqrt{25} < -\sqrt{24,01}$
$-\sqrt{53} < -7 < -6 < -5 < -\sqrt{24,01}$
Ответ: −7; −6; −5.

4) $2,7 = \sqrt{7,29}$
$-\sqrt{31} < -\sqrt{25} < -\sqrt{16} < -\sqrt{9} < -\sqrt{4} < -\sqrt{1} < -\sqrt{0} < \sqrt{1} < \sqrt{4} < \sqrt{7,29}$
$-\sqrt{31} < -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < \sqrt{7,29}$

Ответ: −5; −4; −3; −2; −1; 0; 1; 2.

917. Дана функция
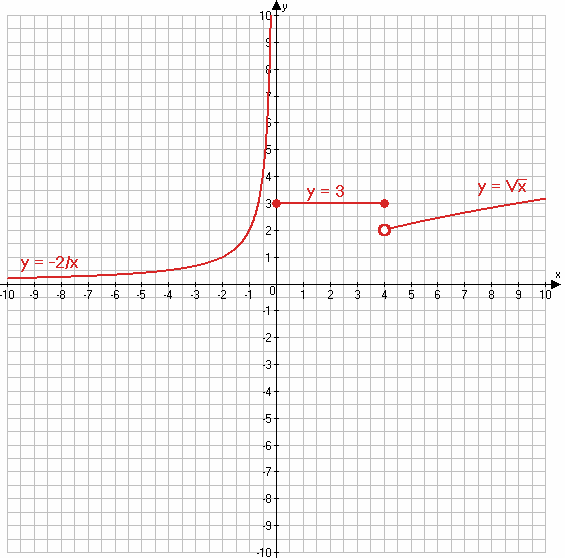
$ƒ(x) = \begin{equation*} \begin{cases} -\frac{2}{x}, если\;x < 0 &\\ 3, если\; 0 ≤ x ≤ 4 &\\ \sqrt{x}, если\;x > 4 & \end{cases} \end{equation*}$
1) Найдите ƒ(−0,5), ƒ(0), ƒ(4), ƒ(9).
2) Постройте график данной функции.

Решение:

1)
$f(-0,5) = -\frac{2}{-0,5} = 4$
$f(0) = 3$
$f(4) = 3$
$f(9) = \sqrt{9} = 3$
2)