Ответы к странице 103
406. Решите уравнение:
1) $\sqrt{17 + \sqrt{\sqrt{x} - 6}} = 5$;
2) $\sqrt{1 + \sqrt{2 + \sqrt{x}}} = 1$.
Решение:
1) $\sqrt{17 + \sqrt{\sqrt{x} - 6}} = 5$
имеет смысл при:
x ≥ 0
и
$\sqrt{x} - 6 ≥ 0$
$(\sqrt{17 + \sqrt{\sqrt{x} - 6}})^2 = 5^2$
$17 + \sqrt{\sqrt{x} - 6} = 25$
$\sqrt{\sqrt{x} - 6} = 25 - 17$
$\sqrt{\sqrt{x} - 6} = 8$
$(\sqrt{\sqrt{x} - 6})^2 = 8^2$
$\sqrt{x} - 6 = 64$
$\sqrt{x} = 64 + 6$
$\sqrt{x} = 70$
$(\sqrt{x})^2 = 70^2$
x = 4900
4900 ≥ 0
и
$\sqrt{4900} - 6 ≥ 0$
70 − 6 ≥ 0
64 ≥ 0
Ответ: 4900
2) $\sqrt{1 + \sqrt{2 + \sqrt{x}}} = 1$
имеет смысл при:
x ≥ 0
$(\sqrt{1 + \sqrt{2 + \sqrt{x}}})^2 = 1^2$
$1 + \sqrt{2 + \sqrt{x}} = 1$
$\sqrt{2 + \sqrt{x}} = 1 - 1$
$\sqrt{2 + \sqrt{x}} = 0$
$2 + \sqrt{x} = 0$
$\sqrt{x} = -2$ − нет корней
Ответ: нет корней
407. При каких значениях a и b имеет смысл выражение:
1) $\sqrt{ab}$;
2) $\sqrt{-ab}$;
3) $\sqrt{ab^2}$;
4) $\sqrt{a^2b^2}$;
5) $\sqrt{-a^2b}$?
Решение:
1) $\sqrt{ab}$
имеет смысл, если:
a и b − числа оба неотрицательные a ≥ 0 и b ≥ 0
или
a и b − числа оба неположительные a ≤ 0 и b ≤ 0
2) $\sqrt{-ab}$
имеет смысл, если a и b имеют разные знаки или равны нулю:
a ≥ 0 и b ≤ 0
или
a ≤ 0 и b ≥ 0
3) $\sqrt{ab^2}$
имеет смысл, если число a неотрицательно, а b − любое число:
a ≥ 0 и b − любое число.
4) $\sqrt{a^2b^2}$
имеет смысл, при любых значениях a и b
5) $\sqrt{-a^2b}$
имеет смысл, если число b неположительное, a − любое число:
a − любое число и b ≤ 0
408. Можно ли утверждать, что при любом значении x имеет смысл выражение:
1) $\sqrt{x^2 - 4x + 4}$;
2) $\sqrt{x^2 - 4x + 5}$?
Решение:
1) $\sqrt{x^2 - 4x + 4} = \sqrt{(x - 2)^2}$
так как подкоренное выражение $(x - 2)^2 ≥ 0$, то можно утверждать, что выражение имеет смысл при любом значении x.
2) $\sqrt{x^2 - 4x + 5} = \sqrt{(x^2 - 4x + 4) + 1} = \sqrt{(x - 2)^2} + 1$
так как $(x - 2)^2 ≥ 0$ и 1 > 0, то подкоренное выражение $(x - 2)^2 + 1 ≥ 0$, значит можно утверждать, что выражение имеет смысл при любом значении x.
409. Докажите, что не существует такого значения x, при котором имеет смысл выражение $\sqrt{-x^2 + 6x - 12}$.
Решение:
$\sqrt{-x^2 + 6x - 12} = \sqrt{-(x^2 - 6x + 12)} = \sqrt{-(x^2 - 6x + 9 + 3)} = \sqrt{-(x^2 - 6x + 9) - 3} = \sqrt{-(x - 3)^2 - 3}$
так как $(x - 3)^2 ≥ 0$, то $-(x - 3)^2 ≤ 0$, также −3 < 0, значит подкоренное выражение $-(x - 3)^2 - 3 ≤ 0$, следовательно не существует такого значения x, при котором имеет смысл выражение.
410. Какое из данных выражений имеет смысл при любом значении x:
1) $\sqrt{x^2 + 8x + 15}$;
2) $\sqrt{x^2 - 10x + 27}$?
Решение:
1) $\sqrt{x^2 + 8x + 15} = \sqrt{x^2 + 8x + 16 - 1} = \sqrt{(x + 4)^2 - 1}$ − не имеет смысл при любом значении x, так как при $(x + 4)^2 < 1$, подкоренное выражение $(x + 4)^2 -1$ будет отрицательным.
2) $\sqrt{x^2 - 10x + 27} = \sqrt{x^2 - 10x + 25 + 2} = \sqrt{(x - 5)^2 + 2}$ − имеет смысл при любом значении x, так как $(x - 5)^2 ≥ 0$ и 2 > 0, значит подкоренное выражение будет всегда неотрицательным.
411. Решите уравнение:
1) $\sqrt{x} = -x$;
2) $\sqrt{x} + \sqrt{x - 1} = 0$;
3) $\sqrt{x^2 - x} + \sqrt{x - 1} = 0$;
4) $\sqrt{x^2 + 2x} + \sqrt{x^2 - 4} = 0$;
5) $(x - 1)\sqrt{x + 1} = 0$;
6) $(x + 1)\sqrt{x - 1} = 0$.
Решение:
1) $\sqrt{x} = -x$
имеет смысл при x ≥ 0
$\sqrt{x} + x = 0$
$\sqrt{x}(1 + \sqrt{x}) = 0$
$\sqrt{x} = 0$
x = 0
или
$1 + \sqrt{x} = 0$
$\sqrt{x} = -1$ − нет корней
Ответ: 0
2) $\sqrt{x} + \sqrt{x - 1} = 0$
имеет смысл при:
x ≥ 0
и
x − 1 ≥ 0
x ≥ 1
$\sqrt{x} = -\sqrt{x - 1}$
$(\sqrt{x})^2 = (-\sqrt{x - 1})^2$
x = x − 1
x − x = −1
0 = −1 − нет корней
Ответ: нет корней
3) $\sqrt{x^2 - x} + \sqrt{x - 1} = 0$
имеет смысл при:
$x^2 - x ≥ 0$
x(x − 1) ≥ 0
x ≥ 0
и
x − 1 ≥ 0
x ≥ 1
$\sqrt{x^2 - x} = -\sqrt{x - 1}$
$(\sqrt{x^2 - x})^2 = (-\sqrt{x - 1})^2$
$x^2 - x = x - 1$
$x^2 - x - x + 1= 0$
$x^2 - 2x + 1= 0$
$(x - 1)^2 = 0$
x − 1 = 0
x = 1
Ответ: 1
4) $\sqrt{x^2 + 2x} + \sqrt{x^2 - 4} = 0$
имеет смысл при:
$x^2 + 2x ≥ 0$
x(x + 2) ≥ 0
x ≥ 0
и
x + 2 ≥ 0
x ≥ −2
и
$x^2 - 4 ≥ 0$
$x^2 ≥ 4$
x ≥ ±2
$\sqrt{x^2 + 2x} = -\sqrt{x^2 - 4}$
$(\sqrt{x^2 + 2x})^2 = (-\sqrt{x^2 - 4})^2$
$x^2 + 2x = x^2 - 4$
$x^2 - x^2 + 2x + 4 = 0$
2x + 4 = 0
2x = −4
x = −2
Ответ: −2
5) $(x - 1)\sqrt{x + 1} = 0$
имеет смысл при
x + 1 ≥ 0
x ≥ −1
x − 1 = 0
x = 1
или
$\sqrt{x + 1} = 0$
$(\sqrt{x + 1})^2 = 0^2$
x + 1 = 0
x = −1
Ответ: −1 и 1
6) $(x + 1)\sqrt{x - 1} = 0$
имеет смысл при
x − 1 ≥ 0
x ≥ 1
x + 1 = 0
x = −1 − не подходит
или
$\sqrt{x - 1} = 0$
$(\sqrt{x - 1})^2 = 0^2$
x − 1 = 0
x = 1
Ответ: 1
412. Решите уравнение:
1) $\sqrt{x} + \sqrt{-x} = 0$;
2) $\sqrt{x} + \sqrt{-x} = 1$;
3) $\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 1} = 0$;
4) $(x - 2)\sqrt{x - 3} = 0$.
Решение:
1) $\sqrt{x} + \sqrt{-x} = 0$
имеет смысл при
$\begin{equation*} \begin{cases} x ≥ 0 &\\ -x ≥ 0 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x ≤ 0 & \end{cases} \end{equation*}$
следовательно уравнение имеет смысл только при x = 0.
Ответ: 0
2) $\sqrt{x} + \sqrt{-x} = 1$
имеет смысл при
$\begin{equation*} \begin{cases} x ≥ 0 &\\ -x ≥ 0 & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} x ≥ 0 &\\ x ≤ 0 & \end{cases} \end{equation*}$
следовательно уравнение имеет смысл только при x = 0, однако
$\sqrt{0} + \sqrt{0} = 1$
0 + 0 ≠ 1, значит уравнение не имеет корней.
Ответ: нет корней
3) $\sqrt{x^2 - 2x + 1} + \sqrt{x^2 - 1} = 0$
$\sqrt{(x - 1)^2} + \sqrt{x^2 - 1} = 0$
имеет смысл при
$x^2 - 1 ≥ 0$
$x^2 ≥ 1$
x ≥ ±1
$\sqrt{(x - 1)^2} = -\sqrt{x^2 - 1}$
$(\sqrt{(x - 1)^2})^2 = (-\sqrt{x^2 - 1})^2$
$(x - 1)^2 = x^2 - 1$
$x^2 - 2x + 1 - x^2 = -1$
−2x = −1 − 1
−2x = −2
x = 1
Ответ: 1
4) $(x - 2)\sqrt{x - 3} = 0$
имеет смысл при
x − 3 ≥ 0
x ≥ 3
x − 2 = 0
x = 2 − не подходит, так как 2 < 3
или
$\sqrt{x - 3} = 0$
x − 3 = 0
x = 3
Ответ: 3
413. При каком значении a уравнение $x^2 = a + 1$:
1) имеет два корня;
2) имеет один корень;
3) не имеет корней?
Решение:
$x^2 = a + 1$
1) уравнение имеет два корня, если a + 1 > 0, то есть при a > −1.
2) уравнение имеет один корень, если a + 1 = 0, то есть при a = −1.
3) уравнение не имеет корней, если a + 1 < 0, то есть при a < −1.
414. Постройте график функции:
1) $y = \sqrt{-x^2}$;
2) $y = \sqrt{-x^2 - 4x - 4} + 2$;
3) $y = (\sqrt{x})^2$.
Решение:
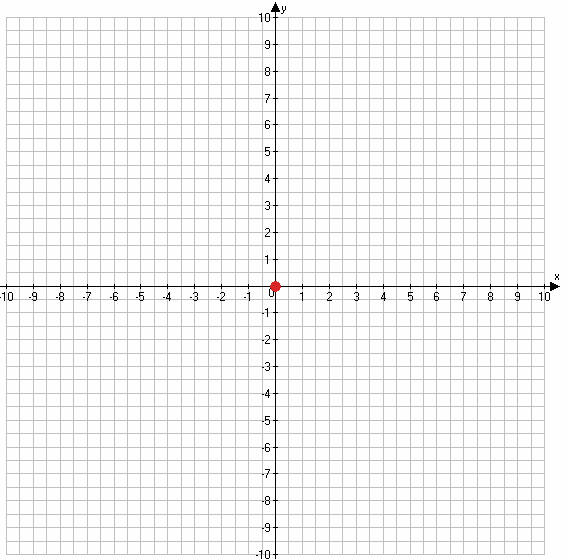
1) $y = \sqrt{-x^2}$
имеет смысл при x = 0, тогда:
$y = \sqrt{0^2}$
y = 0
если x = 0, y = 0, то графиком данной функции является точка (0;0).
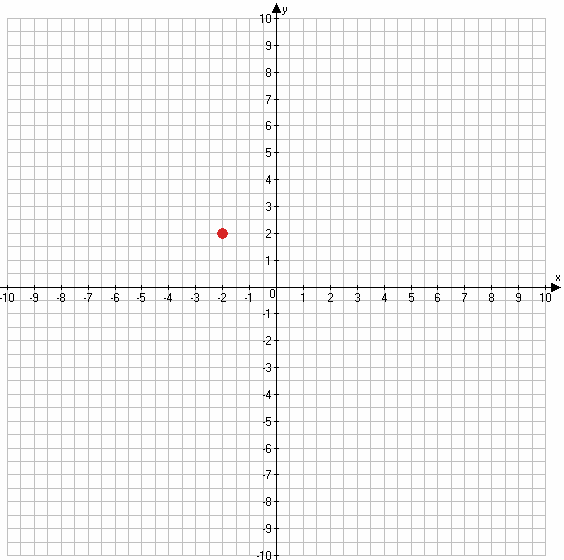
2) $y = \sqrt{-x^2 - 4x - 4} + 2$
$y = \sqrt{-(x^2 + 4x + 4)} + 2$
$y = \sqrt{-(x + 2)^2} + 2$
имеет смысл при
$-(x + 2)^2 ≥ 0$
$(x + 2)^2 ≤ 0$
x + 2 ≤ 0
x ≤ −2
$y = \sqrt{-(-2 + 2)^2} + 2$
$y = \sqrt{0^2} + 2$
y = 2
если x = −2, y = 2, то графиком данной функции является точка (−2;2).
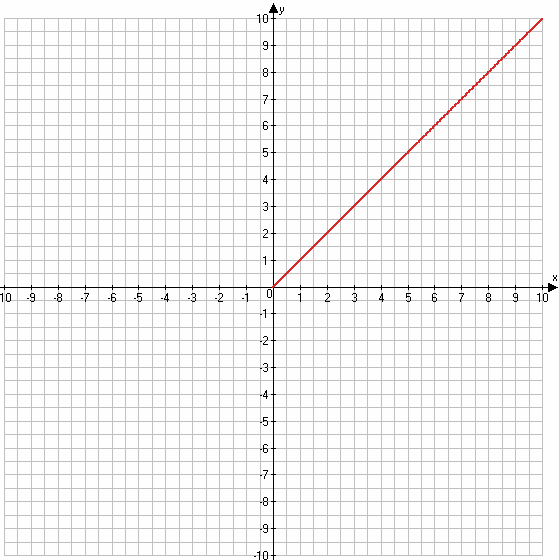
3) $y = (\sqrt{x})^2$
имеет смысл при
x ≥ 0
y = x
415. Постройте график функции $y = \sqrt{2x - 1 - x^2} - 1$.
Решение:
$y = \sqrt{2x - 1 - x^2} - 1$
$y = \sqrt{-x^2 + 2x - 1} - 1$
$y = \sqrt{-(x^2 - 2x + 1)} - 1$
$y = \sqrt{-(x - 1)^2} - 1$
имеет смысл при:
$-(x - 1)^2 ≥ 0$
$(x - 1)^2 ≤ 0$
x − 1 ≤ 0
x ≤ 1
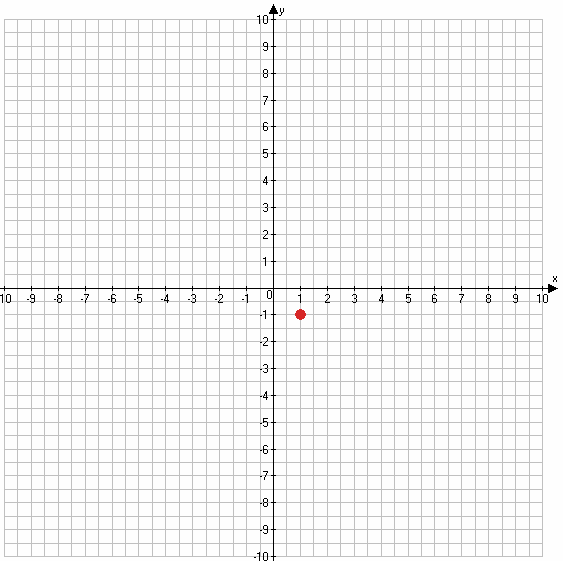
$y = \sqrt{-(1 - 1)^2} - 1$
$y = \sqrt{0^2} - 1$
y = −1
если x = 1, y = −1, то графиком данной функции является точка (1;−1).
416. Для каждого значения a решите уравнение:
1) $a\sqrt{x - 1} = 0$;
2) $\sqrt{(a - 1)x}$;
3) $a\sqrt{x - 1} = a$;
4) $\sqrt{x - 2} = a$.
Решение:
1) $a\sqrt{x - 1} = 0$
имеет смысл при
x − 1 ≥ 0
x ≥ 1
если a = 0, то:
$0 * \sqrt{x - 1} = 0$ при всех допустимых значениях x.
если a ≠ 0, то:
$\sqrt{x - 1} = 0$
x − 1 = 0
x = 1
Ответ:
при a = 0: x ≥ 1;
при a ≠ 0: x = 1.
2) $\sqrt{(a - 1)x}$
имеет смысл при:
(a − 1)x ≥ 0
неравенство будет верным, если оба множителя будут либо неотрицательными, либо неположительными.
(a − 1)x = 0
a − 1 = 0
a = 1
или
x = 0
если a = 1, то:
(1 − 1)x = 0
0x = 0
0 = 0, значит x − любое число.
если a ≠ 1, то:
(a − 1)x = 0
x = 0
Ответ:
при a = 1: x − любое число;
при a ≠ 1: x = 0.
3) $a\sqrt{x - 1} = a$
имеет смысл при
x − 1 ≥ 0
x ≥ 1
если a = 0, то:
$0 * \sqrt{x - 1} = 0$
0 = 0, значит x ≥ 1
если a ≠ 0, то:
$a\sqrt{x - 1} = a$
$\sqrt{x - 1} = \frac{a}{a}$
$\sqrt{x - 1} = 1$
x − 1 = 1
x = 1 + 1
x = 2
Ответ:
при a = 0: x ≥ 1;
при a ≠ 0: x = 2.
4) $\sqrt{x - 2} = a$
имеет смысл при
x − 2 ≥ 0
x ≥ 2
если a < 0, то:
$\sqrt{x - 2} < 0$ − нет корней.
если a ≥ 0, то:
$\sqrt{x - 2} = a$
$(\sqrt{x - 2})^2 = a^2$
$x - 2 = a^2$
$x = a^2 + 2$
Ответ:
при a < 0: корней нет;
при a ≥ 0: $x = a^2 + 2$.
417. При каких значениях a уравнение $(\sqrt{x} - 1)(x - a) = 0$ имеет только один корень?
Решение:
$(\sqrt{x} - 1)(x - a) = 0$
$\sqrt{x} - 1 = 0$
$\sqrt{x} = 1$
x = 1
или
x − a = 0
x = a
уравнение имеет смысл при x ≥ 0, поэтому если a ≤ 0, то корень x = a не подходит, следовательно уравнение будет иметь один корень x = 1.
Ответ: уравнение имеет один корень при a = 1 или при a < 0.