Ответы к странице 115

454. Какие фигуры могут быть пересечением двух лучей, лежащих на одной прямой?

Решение:

Пересечением двух лучей, лежащих на одной прямой, может быть:
1) точка

2) отрезок

3) луч

455. Какие из следующих утверждений верны:
1) {a, b} ∩ {b} = {a, b};
2) {a, b} ∩ {b} = {b};
3) {a, b} ∩ {a} = {a};
4) {a, b} ∩ {b} = {{b}}?

Решение:

1) {a, b} ∩ {b} = {a, b} − верно

2) {a, b} ∩ {b} = {b} − ложно

3) {a, b} ∩ {a} = {a} − ложно

4) {a, b} ∩ {b} = {{b}} − ложно

456. Найдите объединение множеств A и B, если:
1) A − множество равнобедренных треугольников, B − множество равносторонних треугольников;
2) A − множество простых чисел, B − множество составных чисел;
3) A − множество простых чисел, B − множество нечетных чисел.

Решение:

1) AUB = A − множество равнобедренных треугольников

2) AUB − множество всех натуральных чисел, кроме числа 1

3) AUB − множество нечетных чисел и число 2

457. Какие фигуры могут быть объединением двух лучей, лежащих на одной прямой?

Решение:

Объединением двух лучей, лежащих на одной прямой, могут быть прямая или луч.

458. Опишите на языке "необходимо и достаточно" принадлежность элемента x множествам:
1) A и B (рис.25,a);
2) A, B и C (рис.25,б,в).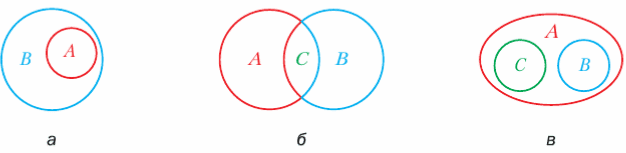

Решение:

1) а) Чтобы элемент x принадлежал множеству B, достаточно, чтобы он принадлежал множеству A.

2) б) Чтобы элемент x принадлежал множеству C, необходимо, чтобы он принадлежал и множеству A и множеству B.
в) Чтобы элемент x принадлежал множеству A, достаточно, чтобы он принадлежал одному из множеств: A или B.

459. Вместо точек поставьте слово "необходимо" или "достаточно", чтобы образовалось верное утверждение:
1) для того чтобы треугольник был равносторонним, ..., чтобы два его угла были равны;
2) для того чтобы четырехугольник был параллелограммом, ..., чтобы две его стороны были параллельны;
3) для того чтобы число делилось нацело на 3, ..., чтобы оно делилось нацело на 9;
4) для того чтобы последняя цифра десятичной записи числа была нулем, ..., чтобы число было кратным 5.

Решение:

1) Для того чтобы треугольник был равносторонним, достаточно, чтобы два его угла были равны.

2) Для того чтобы четырехугольник был параллелограммом, необходимо, чтобы две его стороны были параллельны.

3) Для того чтобы число делилось нацело на 3, достаточно, чтобы оно делилось нацело на 9.

4) Для того чтобы последняя цифра десятичной записи числа была нулем, необходимо, чтобы число было кратным 5.

460. Упростите выражение:
1) $3a^{-6}b^2 * 0,4a^{-2}b^{-5}$;
2) $\frac{4,8a^2b^{-4}}{0,6a^3b^{-6}}$.

Решение:

1) $3a^{-6}b^2 * 0,4a^{-2}b^{-5} = (3 * 0,4) * a^{-6 - 2}b^{2 - 5} = 1,2a^{-8}b^{-3} = \frac{1,2}{a^8b^3} = \frac{6}{5a^8b^3}$

2) $\frac{4,8a^2b^{-4}}{0,6a^3b^{-6}} = \frac{4,8}{0,6}a^{2 - 3}b^{-4 - (-6)} = \frac{48}{6}a^{-1}b^{-4 + 6} = 8a^{-1}b^{-2} = \frac{8b^2}{a}$