Ответы к странице 149
598. Упростите выражение:
1) $\sqrt{(1 - \sqrt{2})^2}$;
2) $\sqrt{(\sqrt{6} - \sqrt{7})^2}$;
3) $\sqrt{(2\sqrt{5} - 3)^2}$;
4) $\sqrt{(\sqrt{3} - 2)^2} + \sqrt{(3 - \sqrt{3})^2}$.
Решение:
1) $1 = \sqrt{1}$
$\sqrt{1} < \sqrt{2}$
$1 < \sqrt{2}$
тогда:
$\sqrt{(1 - \sqrt{2})^2} = |1 - \sqrt{2}| = -1 + \sqrt{2} = \sqrt{2} - 1$
2) $\sqrt{6} < \sqrt{7}$
тогда:
$\sqrt{(\sqrt{6} - \sqrt{7})^2} = |\sqrt{6} - \sqrt{7}| = -\sqrt{6} + \sqrt{7} = \sqrt{7} - \sqrt{6}$
3) $2\sqrt{5} = \sqrt{4 * 5} = \sqrt{20}$
$3 = \sqrt{9}$
$\sqrt{20} > \sqrt{9}$
$2\sqrt{5} > 3$
тогда:
$\sqrt{(2\sqrt{5} - 3)^2} = |2\sqrt{5} - 3| = 2\sqrt{5} - 3$
4) $2 = \sqrt{4}$
$\sqrt{3} < \sqrt{4}$
$\sqrt{3} < 2$
$3 = \sqrt{9}$
$\sqrt{9} > \sqrt{3}$
$3 > \sqrt{3}$
тогда:
$\sqrt{(\sqrt{3} - 2)^2} + \sqrt{(3 - \sqrt{3})^2} = |\sqrt{3} - 2| + |3 - \sqrt{3}| = 2 - \sqrt{3} + 3 - \sqrt{3} = 5 - 2\sqrt{3}$
599. Упростите выражение:
1) $\sqrt{(\sqrt{5} - 4)^2}$;
2) $\sqrt{(\sqrt{8} - 3)^2} - \sqrt{(\sqrt{2} - 3)^2}$.
Решение:
1) $4 = \sqrt{16}$
$\sqrt{5} < \sqrt{16}$
$\sqrt{5} < 4$
тогда:
$\sqrt{(\sqrt{5} - 4)^2} = |\sqrt{5} - 4| = 4 - \sqrt{5}$
2) $3 = \sqrt{9}$
$\sqrt{8} < \sqrt{9}$
$\sqrt{8} < 3$
$\sqrt{2} < \sqrt{9}$
$\sqrt{2} < 3$
тогда:
$\sqrt{(\sqrt{8} - 3)^2} - \sqrt{(\sqrt{2} - 3)^2} = |\sqrt{8} - 3| - |\sqrt{2} - 3| = 3 - \sqrt{8} - (3 - \sqrt{2}) = 3 - \sqrt{8} - 3 + \sqrt{2} = \sqrt{2} - \sqrt{8} = \sqrt{2} - \sqrt{4 * 2} = \sqrt{2} - 2\sqrt{2} = -\sqrt{2}$
600. Решите уравнение $\sqrt{x} = -x^2$.
Решение:
$\sqrt{x} = -x^2$
ОДЗ: x ≥ 0
$-x^2 ≥ 0$
$x^2 ≤ 0$
x = 0
Ответ: x = 0
601. Дана функция
$ƒ(x) = \begin{equation*} \begin{cases} \frac{4}{x}, если\;x < 0 &\\ \sqrt{x}, если\;x ≥ 0 & \end{cases} \end{equation*}$
1) Найдите: ƒ(−8), ƒ(0), ƒ(9).
2) Постройте график данной функции.
Решение:
1)
$ƒ(x) = \begin{equation*} \begin{cases} \frac{4}{x}, если\;x < 0 &\\ \sqrt{x}, если\;x ≥ 0 & \end{cases} \end{equation*}$
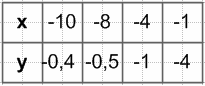
$ƒ(-8) = \frac{4}{-8} = -0,5$
$ƒ(0) = \sqrt{0} = 0$
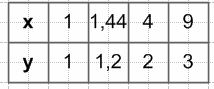
$ƒ(9) = \sqrt{9} = 3$
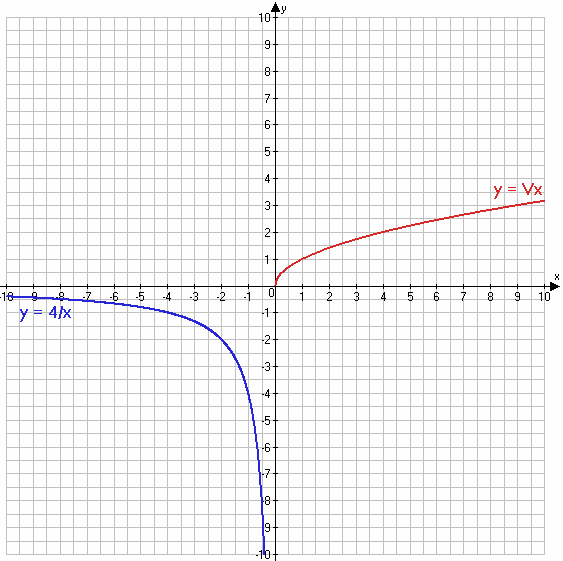
2)
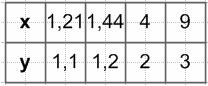
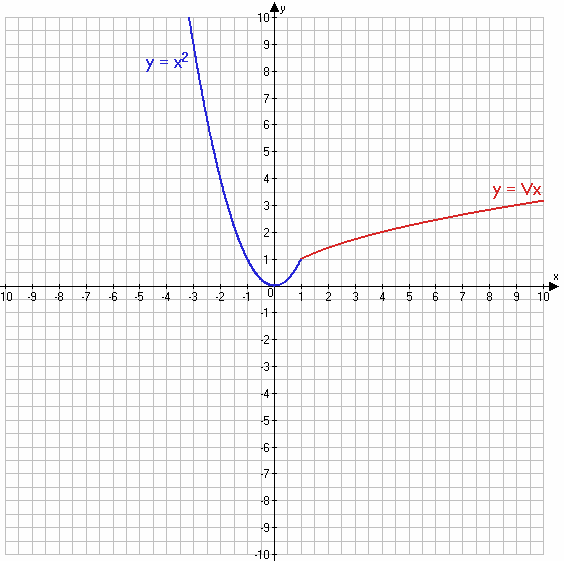
$y = \frac{4}{x}$, если x < 0
$y = \sqrt{x}$, если x ≥ 0
602. Дана функция
$ƒ(x) = \begin{equation*} \begin{cases} x^2, если\;x ≤ 1 &\\ \sqrt{x}, если\;x > 1 & \end{cases} \end{equation*}$
1) Найдите: ƒ(−2), ƒ(0), ƒ(1), ƒ(4).
2) Постройте график данной функции.
Решение:
1)
$ƒ(x) = \begin{equation*} \begin{cases} x^2, если\;x ≤ 1 &\\ \sqrt{x}, если\;x > 1 & \end{cases} \end{equation*}$
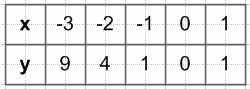
$ƒ(-2) = (-2)^2 = 4$
$ƒ(0) = 0^2 = 0$
$ƒ(1) = 1^2 = 1$
$ƒ(4) = \sqrt{4} = 2$
2)
$y = x^2$, если x ≤ 1
$y = \sqrt{x}$, если x > 1
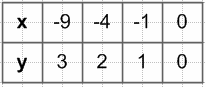
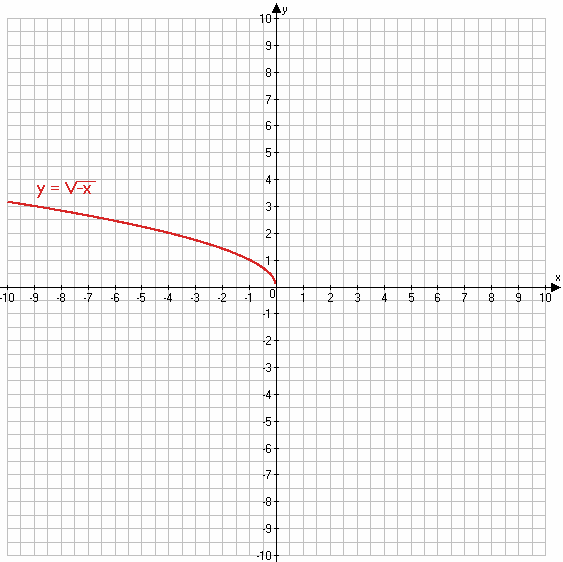
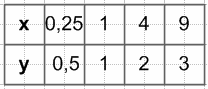
603. Найдите область определения, область значений и нули функции $y = \sqrt{-x}$. Постройте график данной функции.
Решение:
$y = \sqrt{-x}$
Область определения:
−x ≥ 0
x ≤ 0
Область значений:
x ≥ 0
Нули функции:
$\sqrt{-x} = 0$
−x = 0
x = 0
604. Постройте график функции $y = \frac{x}{\sqrt{x}}$.
Решение:
$y = \frac{x}{\sqrt{x}}$
Область определения:
x > 0
Область значений:
y > 0
$y = \frac{x}{\sqrt{x}} = \frac{(\sqrt{x})^2}{\sqrt{x}} = \sqrt{x}$
605. Упростите выражение:
1) $\sqrt{8 - 2\sqrt{7}}$;
2) $\sqrt{5 - 2\sqrt{6}}$;
3) $\sqrt{12 - 6\sqrt{3}}$;
4) $\sqrt{38 - 12\sqrt{2}}$.
Решение:
1) $\sqrt{8 - 2\sqrt{7}} = \sqrt{1 + 7 - 2\sqrt{7}} = \sqrt{1^2 - 2 * 1 * \sqrt{7} + (\sqrt{7})^2} = \sqrt{(1 - \sqrt{7})^2} = |1 - \sqrt{7}| = -1 + \sqrt{7} = \sqrt{7} - 1$
2) $\sqrt{5 - 2\sqrt{6}} = \sqrt{3 + 2 - 2\sqrt{6}} = \sqrt{(\sqrt{3})^2 - 2\sqrt{3 * 2} + (\sqrt{2})^2} = \sqrt{(\sqrt{3} - \sqrt{2})^2} = |\sqrt{3} - \sqrt{2}| = \sqrt{3} - \sqrt{2}$
3) $\sqrt{12 - 6\sqrt{3}} = \sqrt{9 + 3 - 6\sqrt{3}} = \sqrt{3^2 - 2 * 3 * \sqrt{3} + (\sqrt{3})^2} = \sqrt{(3 - \sqrt{3})^2} = |3 - \sqrt{3}| = 3 - \sqrt{3}$
4) $\sqrt{38 - 12\sqrt{2}} = \sqrt{36 + 2 - 12\sqrt{2}} = \sqrt{6^2 - 2 * 6 * \sqrt{2} + (\sqrt{2})^2} = \sqrt{(6 - \sqrt{2})^2} = |6 - \sqrt{2}| = 6 - \sqrt{2}$
606. Упростите выражение:
1) $\sqrt{9 - 4\sqrt{5}}$;
2) $\sqrt{7 - 2\sqrt{10}}$;
3) $\sqrt{37 - 20\sqrt{3}}$.
Решение:
1) $\sqrt{9 - 4\sqrt{5}} = \sqrt{4 + 5 - 4\sqrt{5}} = \sqrt{2^2 - 2 * 2 * \sqrt{5} + (\sqrt{5})^2} = \sqrt{(2 - \sqrt{5})^2} = |2 - \sqrt{5}| = -2 + \sqrt{5} = \sqrt{5} - 2$
2) $\sqrt{7 - 2\sqrt{10}} = \sqrt{5 + 2 - 2\sqrt{10}} = \sqrt{(\sqrt{5})^2 - 2\sqrt{5 * 2} + (\sqrt{2})^2} = \sqrt{(\sqrt{5} - \sqrt{2})^2} = |\sqrt{5} - \sqrt{2}| = \sqrt{5} - \sqrt{2}$
3) $\sqrt{37 - 20\sqrt{3}} = \sqrt{25+ 12 - 20\sqrt{3}} = \sqrt{5^2 - 2 * 5 * 2\sqrt{3} + (2\sqrt{3})^2} = \sqrt{(5 - 2\sqrt{3})^2} = |5 - 2\sqrt{3}| = 5 - 2\sqrt{3}$
607. Сколько корней имеет уравнение $\sqrt{x} = a - x$ в зависимости от значения a?
Решение:
$\sqrt{x} = a - x$
$\sqrt{x} + x = a$
$\sqrt{x}(1 + \sqrt{x}) = a$
при a = 0:
$\sqrt{x}(1 + \sqrt{x}) = 0$
$\sqrt{x} = 0$
$x = 0$
или
$1 + \sqrt{x} = 0$
$\sqrt{x} = -1$
при a < 0:
еcли a < 0, то $\sqrt{x} + x < 0$, что невозможно, так как x ≥ 0, поэтому при a < 0 нет корней.
при a > 0:
если a > 0, то уравнение имеет 1 корень.
Ответ:
при a = 0: x = 0;
при a < 0: корней нет;
при a > 0: один корень.
608. Упростите выражение
$\sqrt{(\sqrt{a} + 1)^2 - 4\sqrt{a}} + \sqrt{(\sqrt{a} - 2)^2 + 8\sqrt{a}}$.
Решение:
$\sqrt{(\sqrt{a} + 1)^2 - 4\sqrt{a}} + \sqrt{(\sqrt{a} - 2)^2 + 8\sqrt{a}} = \sqrt{(\sqrt{a})^2 + 2\sqrt{a} + 1^2 - 4\sqrt{a}} + \sqrt{(\sqrt{a})^2 - 2 * 2\sqrt{a} + 2^2 + 8\sqrt{a}} = \sqrt{a + 2\sqrt{a} + 1 - 4\sqrt{a}} + \sqrt{a - 4\sqrt{a} + 4 + 8\sqrt{a}} = \sqrt{a - 2\sqrt{a} + 1} + \sqrt{a + 4\sqrt{a} + 4} = \sqrt{(\sqrt{a})^2 - 2\sqrt{a} + 1^2} + \sqrt{(\sqrt{a})^2 + 2 * 2\sqrt{a} + 2^2} = \sqrt{(\sqrt{a} - 1)^2} + \sqrt{(\sqrt{a} + 2)^2} = |\sqrt{a} - 1| + |\sqrt{a} + 2|$
т.к. a ≥ 0, то $\sqrt{a} + 2 > 0$
1)
$\sqrt{a} - 1 ≥ 0$
$\sqrt{a} ≥ 0$ и a ≥ 1
$\sqrt{a} + 2 ≥ 0$
$|\sqrt{a} - 1| + |\sqrt{a} + 2| = \sqrt{a} - 1 + \sqrt{a} + 2 = 2\sqrt{a} + 1$
2)
если $\sqrt{a} - 1 < 0$, то есть $\sqrt{a} < 1, 0 < a < 1$
$|\sqrt{a} - 1| + |\sqrt{a} + 2| = -\sqrt{a} + 1 + \sqrt{a} + 2 = 3$
Ответ:
при a ≥ 1 выражение равно $2\sqrt{a} + 1$;
при 0 < a < 1 значение выражения равно 3.
609. Упростите выражение
$\sqrt{(\sqrt{a} - 6)^2 + 24\sqrt{a}} - \sqrt{(\sqrt{a} + 6)^2 - 24\sqrt{a}}$.
Решение:
$\sqrt{(\sqrt{a} - 6)^2 + 24\sqrt{a}} - \sqrt{(\sqrt{a} + 6)^2 - 24\sqrt{a}} = \sqrt{(\sqrt{a})^2 - 2 * 6\sqrt{a} + 6^2 + 24\sqrt{a}} - \sqrt{(\sqrt{a})^2 + 2 * 6\sqrt{a} + 6^2 - 24\sqrt{a}} = \sqrt{a - 12\sqrt{a} + 36 + 24\sqrt{a}} - \sqrt{a + 12\sqrt{a} + 36 - 24\sqrt{a}} = \sqrt{a + 12\sqrt{a} + 36} - \sqrt{a - 12\sqrt{a} + 36} = \sqrt{(\sqrt{a})^2 + 2 * 6\sqrt{a} + 6^2} - \sqrt{(\sqrt{a})^2 - 2 * 6\sqrt{a} + 6^2} = \sqrt{(\sqrt{a} + 6)^2} - \sqrt{(\sqrt{a} - 6)^2} = |\sqrt{a} + 6| - |\sqrt{a} - 6|$
т.к. a ≥ 0, тогда $\sqrt{a} + 6 > 0$
1)
$\sqrt{a} - 6 ≥ 0$
$\sqrt{a} ≥ 6$
a ≥ 36
$|\sqrt{a} + 6| - |\sqrt{a} - 6| = \sqrt{a} + 6 - \sqrt{a} + 6 = 12$
2)
$\sqrt{a} - 6 < 0$
$\sqrt{a} < 6$
0 < a < 36
$|\sqrt{a} + 6| - |\sqrt{a} - 6| = \sqrt{a} + 6 - (-\sqrt{a} + 6) = \sqrt{a} + 6 + \sqrt{a} - 6 = 2\sqrt{a}$
Ответ:
при a ≥ 36 значение выражения равно 12;
при 0 < a < 36 значение выражения равно $2\sqrt{a}$.