Ответы к странице 158
Ответы к параграфу 26. Цилиндр, конус, шар
Задание №767
Приведите примеры предметов, имеющих форму:
1) цилиндра;
2) конуса;
3) шара.
Решение
1) Бочка, кружка, труба.
2) Колпак, морковь, стаканчик мороженого, пожарное ведро.
3) Яблоко, мяч, мыльный пузырь.
Задание №768
На рисунке 65 изображен цилиндр. Укажите:
1) образующую цилиндра;
2) радиус нижнего основания цилиндра;
3) радиус верхнего основания цилиндра.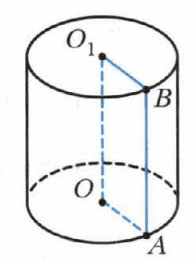
Решение
1) AB − образующая цилиндра
2) OA − радиус нижнего основания цилиндра
3) O1B − радиус верхнего основания цилиндра
Задание №769
Радиус основания цилиндра равен 6 см, а его образующая − 8 см. Найдите площадь боковой поверхности цилиндра.
Решение
Sб = 2πrl = 2π∗6∗8 = 96π $см^2$ ≈ 301,44 $см^2$
Задание №770
Найдите площадь боковой поверхности цилиндра, развертка которого изображена на рисунке 66 (длины отрезков даны в сантиметрах).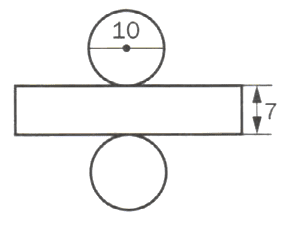
Решение
Sб = 2πrl = 2π∗5∗7 = 70π $см^2$ ≈ 219,8 $см^2$
Задание №771
На рисунке 67 изображен конус. Укажите:
1) вершину конуса;
2) центр его основания;
3) образующую конуса;
4) радиус основания конуса;
5) высоту конуса.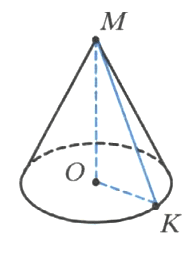
Решение
1) M − вершина конуса
2) O − центр основания конуса
3) MK − образующая конуса
4) OK − радиус основания конуса
5) OM − высота конуса
Задание №772
Радиус шара равен 6 см. Вычислите площадь сечения шара плоскостью, проходящей через центр шара.
Решение
Sсечения = πr2 = π∗62 = 36π $см^2$ ≈ 113,04 $см^2$
Задание №773
Длина окружности, ограничивающей сечение шара плоскостью, проходящей через его центр, равна 12,56 см. Чему равен радиус шара?
Решение
l = 2πr, тогда:
$r=\frac l{2{\operatorname\pi}}=\frac{12,56}{6,28}=2$ см радиус шара.
Задание №774
Какие наименьшие размеры, выраженные целым числом сантиметров, должен иметь прямоугольный лист бумаги, чтобы им можно было обклеить боковую поверхность цилиндра с радиусом основания 5 см и высотой, равной диаметру основания?
Решение
r = 5 см, тогда:
l = 2r = 2 * 5 = 10 см;
Sб = 2πrl = 2π∗5∗10 = 100π $см^2$ ≈ 314 $см^2$;
314 : 10 = 31,4 см, а это значит, что прямоугольный лист бумаги должен иметь размеры 10 см на 32 см.

