Ответы к странице 186

Задание №865

На координатной прямой отметили точки A(2) и B(8). Какую координату должна иметь точка M, чтобы отрезок BM был в 2 раза длиннее отрезка AM? Сколько решений имеет задача?

Решение

1) 

2)

Ответ: M(20) или M(4).

Задание №866

Начертите две окружности, радиусы которых равны 2 см, так, чтобы они:
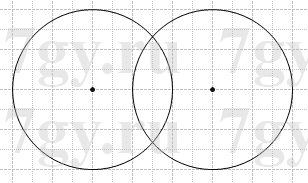
1) имели две общие точки;
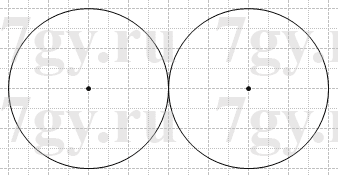
2) имели одну общую точку;
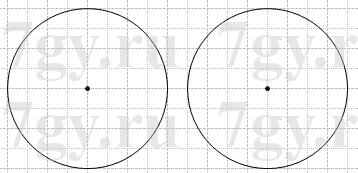
3) не имели общих точек.

Решение

1)

2)

3)

Задание №867

Из некоторого числа вычли 5/17 этого числа и получили 480. Найдите это число.

Решение

Пусть x − искомое число, тогда:
$x-\frac5{17}x=480$
$\frac{12}{17}x=480$
$x=480:\frac{12}{17}$
$x=480\ast\frac{17}{12}$
x = 40 * 17
x = 680 − искомое число.
Ответ: 680.

Задание №868

Все учащиеся 6 класса занимаются или в секции тенниса, или в секции плавания. Некоторые из них занимаются и теннисом, и плаванием: 1/6 теннисистов занимаются плаванием, а 1/5 пловцов − теннисом. Кого в классе больше − теннисистов или пловцов?

Решение

Пусть x − теннисистов и y − пловцов в классе, тогда:
$\frac16x$ теннисистов занимаются плаванием;
$\frac15y$ пловцов занимаются теннисом;
$\frac16x=\frac15y$
$\frac x6=\frac y5$
5x = 6y
$\frac xy=\frac65>1$, следовательно теннисистов в классе больше.
Ответ: теннисистов в классе больше.

Задание №869

Число 50 увеличили на 500%. Во сколько раз полученное число больше 50?

Решение

50 + 50 * 500% = 50 + 50 * 5 = 50 + 250 = 300 − число после увеличения;
300 : 50 = 6, то есть в 6 раз полученное число больше 50.
Ответ: в 6 раз.

Задание №870

На столе стоят семь стаканов − все вверх дном. За один ход разрешается перевернуть любые четыре стакана. Можно ли за несколько ходов добиться того, чтобы все стаканы стояли правильно?

Решение

Так как стаканов нечетное количество, то для того, чтобы все стаканы стояли правильно, их нужно перевернуть нечетное количество раз. По условию задачи, за один раз можно перевернуть четное число стаканов − 4. Следовательно, таким образом нельзя перевернуть все стаканы.
Ответ: перевернуть стаканы по условию задачи нельзя.