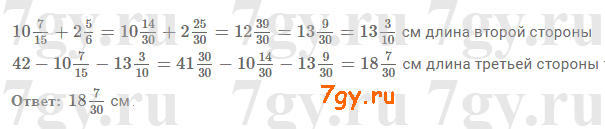Ответы к странице 61

Задача № 298

Длина одной из сторон треугольника равна 12 3/8 см, что на 4 5/24 см больше длины второй стороны и на 3 2/3 см меньше длины третьей. Вычислите периметр треугольника.

Решение задачи

Задача № 299

Периметр треугольника равен 42 см, а длина одной из сторон − 10 7/15 см, что на 2 5/6 см меньше длины второй. Найдите длину третьей стороны треугольника.

Решение от

Задача № 300

Филипок потратил 1/2 своих денег на приобретение книги "Занимательная математика", 1/4 − на книгу "Занимательная физика", 1/12 − на карандаши, а оставшиеся деньги − на конфеты. Какую часть своих денег Филипок потратил на конфеты?

Решение задачи

Задача № 301

Золотов, Серебров, Платинов и Бриллиантов нашли клад. Золотову досталась 1/6 клада, Сереброву − 2/9, Платинову − 5/18, а остальное − Бриллиантову. Какую часть клада получил Бриллиантов?

Решение

Задача № 302

Ивасик−Телесик может вспахать поле за 6 ч, а Катигорошек − за 4 ч. Какую часть поля они вспашут, работая вместе, за 1ч? За 2 ч?

Решение задачи

Задача № 303

Первый маляр может покрасить забор за 15 ч, второй − за 12 ч, а третий − за 10 ч. Какую часть забора они покрасят вместе за 1 ч? За 2 ч? За 4 ч?

Решение

Задание№ 304

1) Миша может съесть арбуз за 12 мин, а Коля − за 16 мин. Какая часть арбуза останется через 1 мин, если мальчики одновременно начнут есть его вместе?
2) Бассейн можно наполнить водой за 6 ч через одну трубу и слить воду за 10 ч через другую. Бассейн был пуст, когда Иван Забывайкин открыл краны одновременно на двух трубах. Какая часть бассейна останется незаполненной водой через 1 ч после того, как открыли краны?

Решение задач

Задача № 305

Петр Ленивцев может покрасить стену за 24 ч, а Иван Трудолюб − за 8 ч. Какая часть стены останется неокрашенной после 1 ч совместной работы Ленивцева и Трудолюба?

Решение задачи

Вся стена равна 1, тогда:
1/24 стены покрасит Петр Ленивцев за 1 ч;
1/8 стены покрасит Иван Трудолюб за 1 ч;
1−1/24−1/8=24/24−1/24−3/24=20/24=5/6 (стены) останется неокрашенной после 1 ч совместной работы Ленивцева и Трудолюба.
Ответ: 5/6 стены.

Задача № 306

Елена и Мария могут вместе набрать на компьютере текст рукописи за 6 ч. Какую часть рукописи наберет Елена за 1 ч, если Мария может набрать текст всей рукописи за 9 ч?

Решение задачи

Вся рукопись равна 1, тогда:
1/6 рукописи наберут Елена и Мария за 1 ч;
1/9 рукописи наберет Мария за 1 ч;
1/6−1/9=3/18−2/18=1/18 часть рукописи наберет Елена за 1 ч.
Ответ: 1/18 часть рукописи.

Задача № 307

Через две трубы бассейн можно наполнить водой за 3 ч. Какую часть бассейна можно наполнить за 1 ч через одну из этих труб, если через другую трубу его можно наполнить за 5 ч?

Решение задачи

Весь бассейн равен 1, тогда:
1/3 часть бассейна можно наполнить через две трубы за 1 ч;
1/5 часть бассейна можно наполнить через одну трубу за 1 ч;
1/3−1/5=5/15−3/15=2/15 части бассейна можно наполнить за 1 ч через вторую трубу.
Ответ: 2/15 части бассейна.