Ответы к странице 255

Задание №1234

На рисунке 124 AС⊥DK, OB⊥BF, ∠DBO = 54°. Вычислите градусную меру угла ABF.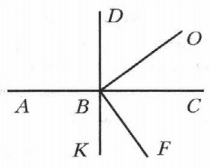

Решение

∠DBK развернутый и равен 180°.
Так как, OB⊥BF, то ∠OBF = 90°, тогда:
∠KBF = ∠DBK − ∠DBO − ∠OBF = 180° − 54° − 90° = 36°.
Так как, AС⊥DK, то ∠ABK = 90°, тогда:
∠ABF = ∠ABK + ∠KBF = 90° + 36° = 126°
Ответ: ∠ABF = 126°

Задание №1235

Как построить перпендикулярные прямые, пользуясь шаблоном угла, который равен:
1) 15°;
2) 18°?

Решение

1) 90 : 15 = 6, следовательно необходимо шаблоном угла 15° отложить 6 последовательных углов.

2) 90 : 18 = 5, следовательно необходимо шаблоном угла 18° отложить 5 последовательных углов.

Задание №1236

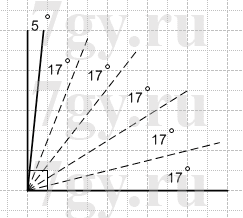
Пользуясь угольником и шаблоном угла 17°, постройте угол, градусная мера которого:
1) 5°;
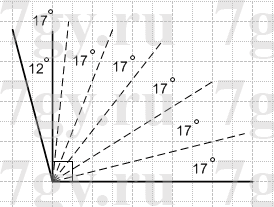
2) 12°?

Решение

1)

90° − 17° * 5 = 90° − 85° = 5°

2)

17° * 6 − 90° = 102° − 90° = 12°

Задание №1237

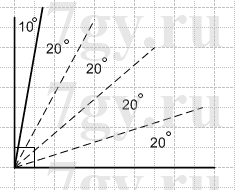
Пользуясь угольником и шаблоном угла 20°, постройте угол, градусная мера которого 10°.

Решение

90° − 20° * 4 = 90° − 80° = 10°

Задание №1238

Сумма цифр двузначного числа равна 8, количество десятков в 3 раза меньше количества единиц. Найдите это число.

Решение

Пусть x количество десятков, тогда:
3x количество единиц.
Так как, сумма цифр двузначного числа равна 8, то:
3x + x = 8
4x = 8
x = 8 : 4
x = 2 количество десятков;
3x = 3 * 2 = 6 количество единиц, следовательно искомое число 26.
Ответ: 26.

Задание №1239

Из семи учащихся четверо хорошо поют, двое выразительно читают стихи, а один красиво танцует. Сколькими способами из этих учащихся можно организовать концертную бригаду, состоящую из певца, чтеца и танцора?

Решение

В концертную бригаду можно выбрать:
одного из четырех певцов (4 способа);
одного из двух чтецов (2 способа);
одного танцора (1 способ), тогда:
4 * 2 * 1 = 8 способами можно организовать концертную бригаду.
Ответ: 8 способов.

Задание №1240

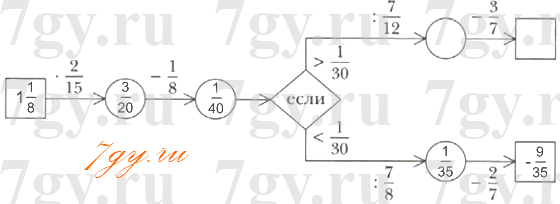
Заполните пропуски в цепочке вычислений при:
1) x = 1 1/8;
2) x = 1 1/4.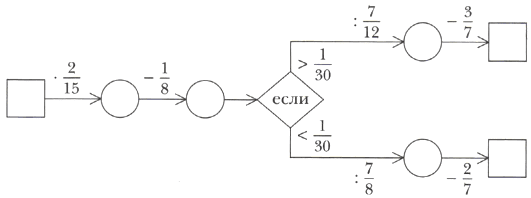

Решение

1) $x\ast\frac2{15}=1\frac18\ast\frac2{15}=\frac98\ast\frac2{15}=\frac34\ast\frac15=\frac3{20}$
$\frac3{20}-\frac18=\frac6{40}-\frac5{40}=\frac1{40}$
$\frac1{40}<\frac1{30}$
$\frac1{40}:\frac78=\frac1{40}\ast\frac87=\frac15\ast\frac17=\frac1{35}$
$\frac1{35}-\frac27=\frac1{35}-\frac{10}{35}=-\frac9{35}$


2) $x\ast\frac2{15}=1\frac14\ast\frac2{15}=\frac54\ast\frac2{15}=\frac12\ast\frac13=\frac16$
$\frac16-\frac18=\frac4{24}-\frac3{24}=\frac1{24}$
$\frac1{24}>\frac1{30}$
$\frac1{24}:\frac7{12}=\frac1{24}\ast\frac{12}7=\frac12\ast\frac17=\frac1{14}$
$\frac1{14}-\frac37=\frac1{14}-\frac6{14}=-\frac5{14}$

Задание №1241

Сегодня Василию Ивановичу исполнилось 80 лет, а его детям − 34, 36 и 40. Сколько лет прошло с того времени, когда возраст отца был в 2 раза больше суммы возрастов его детей?

Решение

Пусть x лет прошло, тогда:
80 − x лет было Василию Ивановичу;
34 − x лет было первому ребенку;
36 − x лет было второму ребенку;
40 − x лет было третьему ребенку.
Так как, возраст отца был в 2 раза больше суммы возрастов его детей, то:
2(34 − x + 36 − x + 40 − x) = 80 − x
2(−3x + 110) = 80 − x
−6x + 220 = 80 − x
−6x + x = 80 − 220
−5x = −140
x = −140 : (−5)
x = 28 лет прошло.
Ответ: 28 лет.

Задание №1242

Верно ли, что |a| + a = 2a при любом значении a?

Решение

Неверно, так как при отрицательном значении a равенство не будет верным, например a = −5, тогда:
|−5| + (−5) = 2 * (−5)
5 − 5 = −10
0 ≠ −10

Задание №1243

На шахматную доску пролили краску. Может ли количество залитых клеток быть на 17 меньше количества клеток, оставшихся чистыми?

Решение

Пусть x клеток залили, тогда:
64 − x клеток остались чистыми.
Представим, что количество залитых клеток на 17 меньше чистых, тогда:
(64 − x) − x = 17
64 − x − x = 17
−2x = 17 − 64
x = −47 : (−2)
x = 23,5 клеток залили, что невозможно, так как количество клеток должно быть натуральным числом, следовательно залитых клеток не может быть на 17 меньше количества клеток, оставшихся чистыми.
Ответ: не может.