Ответы к странице 152

Задание №751

Вычислите площадь закрашенной фигуры (рис. 46), если длина стороны клетки равна 1 см.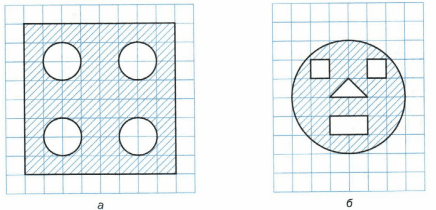

Решение

а) $S_{квадрата}=a^2=8^2=8\ast8=64(см^2)$
$S_{круга}={\operatorname\pi}r^2=3,14\ast1^2=3,14(см^2)$
На рисунке 4 одинаковых круга, поэтому их суммарная площадь:
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}\ast4=3,14\ast4=12,56{\operatorname с}{\operatorname м}^2$
$S_{\operatorname ф\operatorname и\operatorname г\operatorname у\operatorname р\operatorname ы}=S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}-4\ast S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}=64-12,56=51,44{\operatorname с}{\operatorname м}^2$

б)$S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}=a^2=1^2=1{\operatorname с}{\operatorname м}^2$
Треугольник на фигуре можно разделить пополам и сложить из этих половинок квадрат со стороной 1 см;
Прямоугольник состоит из 2 квадратов со стороной 1 см;
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}={\operatorname\pi}r^2=3,14\ast3^2=3,14\ast9=28,26{\operatorname с}{\operatorname м}^2$
$S_{\operatorname ф\operatorname и\operatorname г\operatorname у\operatorname р\operatorname ы}=S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}-5\ast S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}=28,26-5=23,26{\operatorname с}{\operatorname м}^2$

Задание №752

Пицца, диаметр которой равен 30 см, стоит столько же, сколько две пиццы диаметром 20 см. В каком случае Дима съест больше пиццы: если купит одну большую или две маленькие, если все пиццы имеют одинаковую толщину?

Решение

r1 = 30 : 2 = 15 (см) диаметр большой пиццы;
r2 = 20 : 2 = 10 (см) диаметр маленькой пиццы;
$S_1={\operatorname\pi}r_1^2=3,14\ast15^2=3,14\ast225=706,5{\operatorname с}{\operatorname м}^2$ − площадь большой пиццы;
$S_2={\operatorname\pi}r_2^2=3,14\ast10^2=3,14\ast100=314{\operatorname с}{\operatorname м}^2$ − площадь маленькой пиццы, следовательно: 314 * 2 = 628 $см^2$ − суммарная площадь двух маленьких пицц.
706,5 − 628 = 78,5 ($см^2$)
Ответ: Дима съест на 78,5 $см^2$ больше, если купит одну большую пиццу.

Задание №753

Диаметр колеса автомобиля равен 65 см. Автомобиль движется с такой скоростью, что колеса делают шесть оборотов в секунду. Найдите скорость автомобиля в километрах в час. Ответ округлите до десятых.

Решение

l = 2πr = πd = 3,14 * 65 = 204,1 см длина окружности колеса;
204,1 * 6 = 1224,6 см/сек скорость автомобиля в сантиметрах в секунду.
1 ч = 60 мин * 60 с = 3600 секунд;
1 км = 1000 м * 100 см = 100000 см, тогда:
$\frac{1224,6\ast3600}{100000}$ = 44,0856 ≈ 44,1 км/ч.

Задание №754

Диаметр колеса вагона равен 78 см. За 2,5 мин колесо делает 1000 оборотов. Найдите скорость поезда метро в километрах в час. Ответ округлите до десятых.

Решение

l = 2πr = πd = 3,14 * 78 = 244,92 см длина окружности колеса;
244,92 * 1000 : 2,5 = 97968 см/мин скорость поезда метро в сантиметрах в минуту.
1 ч = 60 мин;
1 км = 1000 м * 100 см = 100000 см, тогда:
$\frac{97968\ast60}{100000}$ = 58,7808 ≈ 58,8 км/ч.

Задание №755

Найдите длину дуги, которую описывает часовая стрелка длиной 6 см за 1 ч.

Решение

r = длина часовой стрелки = 6 см;
l = 2πr = 2 * 3,14 * 6 = 37,68 см длина окружности циферблата;
На циферблате 12 дуг по 1 часу, тогда:
37,68 : 12 = 3,14 см длина дуги, которую описывает часовая стрелка длиной 6 см за 1 ч.

Задание №756

Найдите длину дуги, которую описывает минутная стрелка длиной 24 см за 40 мин.

Решение

r = длина часовой стрелки = 24 см;
l = 2πr = 2 * 3,14 * 24 = 150,72 (см) - длина окружности циферблата;
На циферблате 60 дуг по 1 минуте, тогда:
$\frac{40}{60}=\frac23$ - часть циферблата занимает искомая дуга, следовательно:
$150,72\ast\frac23=50,24\ast2=100,48$ (см) - длина дуги, которую описывает минутная стрелка длиной 24 см за 40 мин.

Задание №757

Вычислите площадь закрашенной фигуры, изображенной на рисунке 47.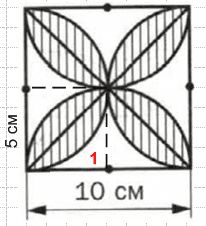

Решение

Найдем площадь не закрашенного участка отмеченного цифрой 1. Данная площадь равна площадь квадрата со стороной 5 см вычесть 1/4 площади окружности со радиусом 5 см, тогда:
$S_1=S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}-\frac14S_{\operatorname о\operatorname к\operatorname р\operatorname у\operatorname ж\operatorname н\operatorname о\operatorname с\operatorname т\operatorname и}=5^2-\frac14\ast3,14\ast5^2=25-\frac{78,5}4=25-19,625=5,375$

Так как, таких не закрашенных участков 8, то 8 * 5,375 = 43 $см^2$ - площадь не закрашенной области на рисунке 47.
Площадь закрашенной фигуры = площадь квадрата со стороной 10 см − площадь не закрашенной области = $10^2-43=100-43=57(см^2)$

Задание №758

Все вершины квадрата (рис. 48), диагональ которого равна 6 см, лежат на окружности. Вычислите площадь квадрата, не измеряя его стороны. На сколько площадь квадрата меньше площади круга, ограниченного данной окружностью?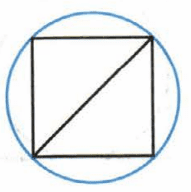

Решение

Диагональ = диаметр окружности, тогда:
r = 6 : 2 = 3 см;
$S_{круга}=\operatorname\pi r^2=3,14\ast3^2=3,14\ast9=28,26(см^2)$;
Квадрат состоит из двух треугольников, площадь каждого из которого равна
$\frac12ah$, где a − основание треугольника, а h − высота треугольника, тогда:
$S_{треугольника}=\frac12\ast6\ast3=3\ast3=9(см^2)$;
$S_{квадрата}=9\ast2=18(см^2)$;
$S_{круга}-S_{квадрата}=28,26-18=10,26(см^2)$
Ответ: на 10,26 $см^2$ площадь квадрата меньше площади круга, ограниченного данной окружностью.