Ответы к странице 159

Задание №775

Диаметр отверстия трубы равен 40 см, а толщина ее стенок − 2 см. Хватит ли 2,5 кг краски, чтобы покрасить снаружи 10 м этой трубы, если на 1 $м^2$ ее поверхности расходуется 200 г краски?

Решение

Наружный диаметр трубы равен сумме диаметра отверстия трубы и толщине двух ее стенок, тогда:
d = 40 + 2 * 2 = 44 см;
r = 44 : 2 = 22 см = 0,22;
Sб = 2πrl = 2π∗0,22∗10 = 3,14∗440 = 13,816 $м^2$ площадь, которую необходимо покрасить;
200 г = 0,2 кг;
13,816 * 0,2 ≈ 2,76 кг краски необходимо, чтобы покрасить 10 м трубы;
2,5 кг < 2,76 кг, следовательно краски не хватит.

Задание №776

Прямоугольник, площадь которого равна 40 $см^2$, вращают вокруг одной из его сторон. Вычислите площадь боковой поверхности образовавшегося цилиндра.

Решение

Sпрямоугольника=ab, а так как прямоугольник вращают вокруг одной из его сторон то
Sпрямоугольника=rl, а
Sб=2πrl, следовательно при любых размерах сторон прямоугольника площадь боковой поверхности образовавшегося цилиндра будет одним и тем же.
Пусть прямоугольник имеет стороны 4 см и 10 см, тогда:
Sб = 2πrl = 2π∗4∗10 = 3,14∗80 = 251,2 $см^2$ площадь боковой поверхности образовавшегося цилиндра.

Задание №777

Хватит ли купленной ковровой дорожки для трех коридоров длиной 22,6 м, 24,7 м и 12,8 м, если купили 2 куска дорожки по 15,8 м и 2 куска по 14,6 м?

Решение

22,6 + 24,7 + 12,8 = 60,1 м суммарная длина коридоров;
2 * 15,7 + 2 * 14,6 = 2 * (15,7 + 14,6) = 2 * 30,4 = 60,8 м суммарная длина дорожки;
60,8 м > 60,1 м, значит дорожки хватит на все три коридора.

Задание №778

Оля живет в двенадцатиэтажном доме в квартире № 189. В каком подъезде и на каком этаже живет Оля, если в ее доме на каждом этаже находится по четыре квартиры?

Решение

12 * 4 = 48 квартир в одном подъезде;
$\frac{189}{48}=3\frac{45}{48}$, следовательно Оля живет в 4 подъезде;
$\frac{45}{48}=11\frac3{48}$, следовательно Оля живет на 12 этаже.

Задание №779

Известно, что a и b − различные простые числа. Запишите все делители числа m, если:
1) m = ab;
2) m = $a^2b$;
3) m = $a^2b^2$.

Решение

1) 1; a; b; m.

2) $1;a;b;a^2;ab;m.$

3) $1;a;b;a^2;b^2;ab;a^2b;ab^2;m.$.

Задание №780

В середине XVI в. в Москве проживало 100000 жителей и она была самым многолюдным городом Московского государства. После столицы по числу жителей выделялись города Великий Новгород и Псков. Количество жителей Пскова составляло 20% от количества жителей Москвы и 80% от количества жителей Великого Новгорода. Сколько людей проживало в середине XVI в. в Великом Новгороде?

Решение

100000 * 20% = 100000 * 0,2 = 20000 жителей было в Пскове;
20000 : 80% = 20000 : 0,8 = 25000 жителей было в Великом Новгороде.

Задание №781

Пусть столбик, высота которого равна стороне клетки тетради, соответствует 1 году жизни человека. Нарисуй столбик, высота которого соответствует твоему возрасту.

Решение

Нарисуй столбик высотой столько клеток, сколько тебе полных лет.

Задание №782

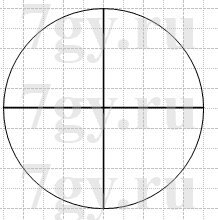
Изобразите круг, разделите его двумя диаметрами на четыре равных сектора. Сколько процентов площади круга составляет площадь одного сектора?

Решение

Весь круг 100%, тогда:
100% : 4 = 25% площади круга составляет площадь одного сектора.

Задание №783

Используя только цифры 1, 2, 3, 4, записали два неравных четырехзначных числа, у каждого из которых все цифры различны. Может ли одно из этих чисел делиться нацело на другое?

Решение

Нет, не может. Если бы это было возможно, то в частном могло получиться либо 2, либо 3. Но при умножении чисел 2 или 3 на цифры, данные в задаче, мы получим цифры, которые не даны, например 6, 8 или 9.