Ответы к странице 153

Задание №759

Докажите, что сумма длин красных дуг равна сумме длин зеленых дуг (рис.49).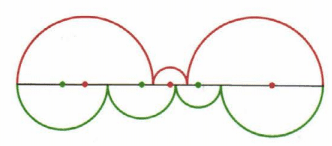

Решение

И красные и зеленые дуги являются полуокружностями длина которой равна πr, тогда:
сумма длин красных дуг равна
πr1+πr2+πr3=π(r1+r2+r3);
сумма длин зеленых дуг равна
πr4+πr5+πr6+πr7=π(r4+r5+r6+r7), а так как: r1 + r2 + r3 = r4 + r5 + r6 + r7, следовательно сумма длин красных дуг равна сумме длин зеленых дуг.

Задание №760

Задача Гиппократа. (Гиппократ Хиосский − древнегреческий геометр (V в. до н.э.).) Докажите, что сумма площадей закрашенных фигур ("луночек") равна площади прямоугольника (рис.50).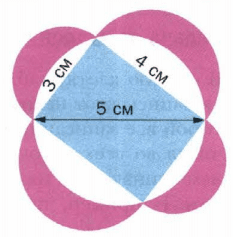

Решение

Найдем площадь не закрашенных участков, которая равна разнице площади окружности с диаметром 5 см и площади прямоугольника:
r=d:2=5:2=2,5;
$S_{\operatorname н\operatorname е\operatorname з\operatorname а\operatorname к\operatorname р.}={\operatorname\pi}r^2-ab=3,14\ast2,5^2-3\ast4=3,14\ast6,25-12=19,625-12=7,625{\operatorname с}{\operatorname м}^2$
Площадь "луночек" = сумма площадей двух полуокружностей с диаметром 3 см и двух полуокружностей с диаметром 4 см − площадь не закрашенных участков, тогда:
$2\ast\frac12{\operatorname\pi}2^2+2\ast\frac12{\operatorname\pi}1,5^2-7,625=3,14\ast(4\ast2,25)-7,625=3,14\ast6,25-7,625=19,625-7,625=12{\operatorname с}{\operatorname м}^2$,
значит сумма площадей закрашенных фигур ("луночек") равна площади прямоугольника.

Задание №761

Два квадрата со стороной 1 см имеют общий центр (центр квадрата − точка пересечения его диагоналей)(рис.51). Докажите, что площадь их общей части больше π/4.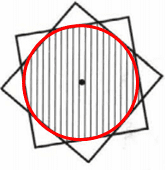

Решение

В общую часть квадратов можно вписать круг.
$r=d:2=\frac12$
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}={\operatorname\pi}r^2={\operatorname\pi}\ast\frac12^2=\frac{\operatorname\pi}4$, а так как площадь круга меньше общей части квадратов, то общая часть квадратов больше π/4.

Задание №762

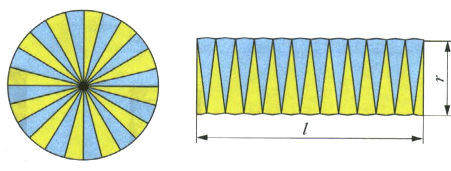
На рисунке 52 проиллюстрирован старинный способ вычисления площади круга. Объясните, почему произведение rl приближенно равно площади круга.

Решение

$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}={\operatorname\pi}r^2$;
l = 2πr, а так как на прямоугольнике синие сектора перевернуты, в отличии их расположения на круге, то l на прямоугольнике равна $\frac{2{\operatorname\pi}r}2={\operatorname\pi}r$, тогда:
${\operatorname\pi}r\ast r={\operatorname\pi}r^2=S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}$