Ответы к странице 146
Задание №716
На рисунке 37 OC = 6 см, BD = 2,5 см. Найдите длину отрезка OK.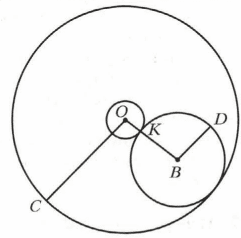
Решение
OB = OC − BD = 6 − 2,5 = 3,5 см;
OK = OB − BD = 3,5 − 2,5 = 1 см.
Задание №717
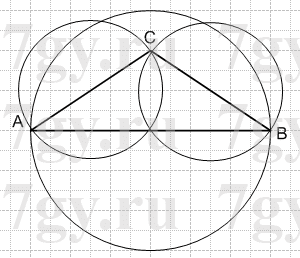
Начертите произвольный треугольник. Проведите три окружности так, чтобы стороны треугольника были их диаметрами.
Решение
Задание №718
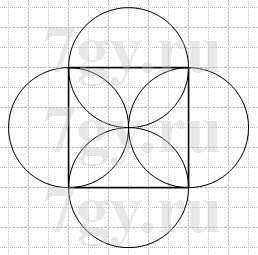
Начертите квадрат со стороной 3 см. Проведите четыре окружности так, чтобы стороны квадрата были их диаметрами.
Решение
Задание №719
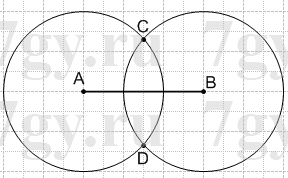
1) Начертите отрезок AB, длина которого равна 3 см. Найдите точку, удаленную от каждого из концов отрезка AB на 2 см. Сколько существует таких точек?
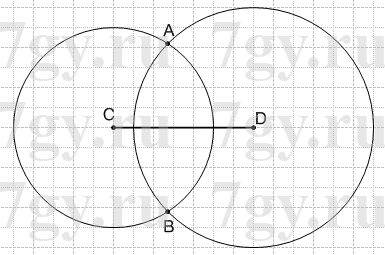
2) Начертите отрезок CD, длина которого равна 3 см 5 мм. Найдите точку, удаленную от точки C на 2 см 5 мм, а от точки D - на 3 см.
Сколько существует таких точек?
Решение
1)
Две точки: C и D;
AC = CB = BD = AD = 2 см.
2)
Две точки: A и B;
AD = DB = 3 см;
AС = СB = 2 см 5 мм.
Задание №720
С помощью циркуля и линейки постройте треугольник со сторонами:
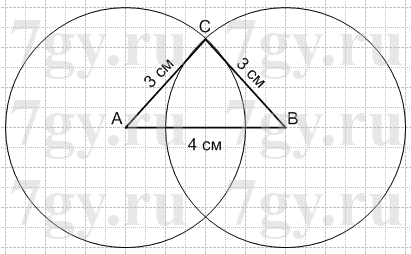
1) 3 см, 3 см и 4 см;
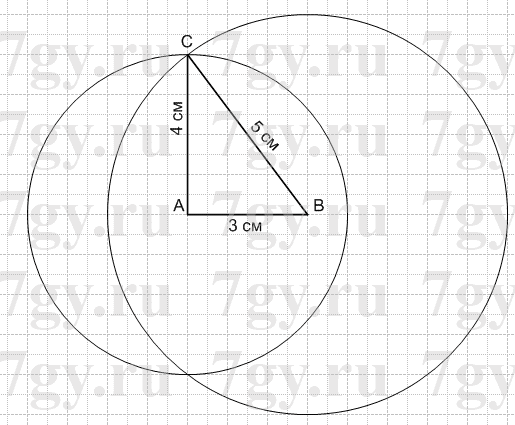
2) 3 см; 4 см и 5 см.
Решение
1) 1 действие: строим отрезок AB = 4 см;
2 действие: строим две окружности, радиус которых равен 3 см, с центрами в точках A и B.
3 действие: точку С ставим в одной любой точке пересечения окружностей;
4 действие: проводим отрезки AC = BC = 3 см.
2) 1 действие: строим отрезок AB = 3 см;
2 действие: строим окружность, с радиусом равным 4 см, с центром в точке A;
3 действие: строим окружность, с радиусом равным 5 см, с центром в точке B;
4 действие: точку С ставим в одной любой точке пересечения окружностей;
5 действие: проводим отрезки AC = 4 см и BC = 5 см.
Задание №721
С помощью циркуля и линейки постройте треугольник со сторонами:
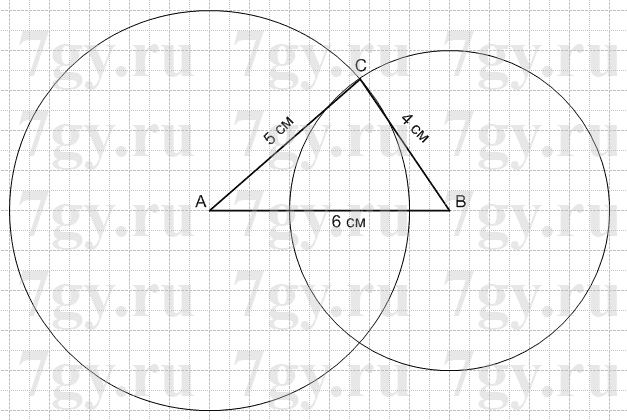
1) 5 см, 6 см и 4 см;
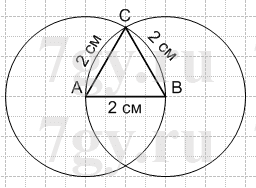
2) 2 см; 2 см и 2 см.
Решение
1) 1 действие: строим отрезок AB = 6 см;
2 действие: строим окружность, с радиусом равным 5 см, с центром в точке A;
3 действие: строим окружность, с радиусом равным 4 см, с центром в точке B;
4 действие: точку С ставим в одной любой точке пересечения окружностей;
5 действие: проводим отрезки AC = 5 см и BC = 4 см.
2) 1 действие: строим отрезок AB = 2 см;
2 действие: строим две окружности, радиус которых равен 2 см, с центрами в точках A и B.
3 действие: точку С ставим в одной любой точке пересечения окружностей;
4 действие: проводим отрезки AC = BC = 2 см.
Задание №722
Установите, можно ли построить треугольник со сторонами:
1) 2 см, 6 см и 7 см;
2) 2 см, 6 см и 8 см;
3) 2 см, 6 см и 9 см.
Решение
1) Для того, чтобы построить треугольник, каждая сторона треугольника должна быть меньше суммы двух других сторон.
2 < 6 + 7;
6 < 2 + 7;
7 < 2 + 6, следовательно треугольник с данными сторонами построить можно.
2) Для того, чтобы построить треугольник, каждая сторона треугольника должна быть меньше суммы двух других сторон.
2 < 6 + 8;
6 < 2 + 8;
8 = 2 + 6, следовательно треугольник с данными сторонами построить нельзя.
3) Для того, чтобы построить треугольник, каждая сторона треугольника должна быть меньше суммы двух других сторон.
2 < 6 + 9;
6 < 2 + 9;
9 > 2 + 6, следовательно треугольник с данными сторонами построить нельзя.
Задание №723
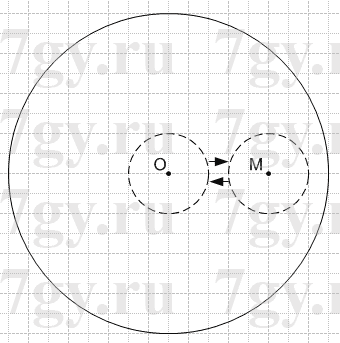
В круге с центром O отметили точку M. Как разрезать этот круг:
1) на три части;
2) на две части − так, чтобы из них можно было составить новый круг, в котором отмеченная точка M была бы его центром?
Решение
1) 1 действие:
Необходимо вырезать два круга с центром в точках O и M, причем радиус вырезаемых кругов должен быть меньше радиуса исходного круга более, чем в три раза.
2 действие:
Вырезанные круги необходимо поменять местами.
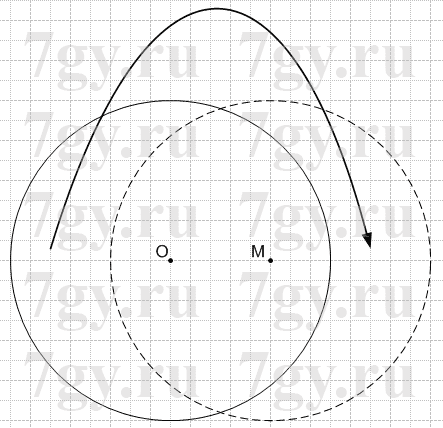
2) 1 действие:
Необходимо построить круг с центром в точке M и радиусом равным радиусу исходного круга с центром в точке O.
2 действие:
Разрезать круг с центром в точке O по дуге, образованной кругом с центром в точке O.
3 действие:
Отрезанные части приложить друг к другу с обратной стороны.
Задание №724
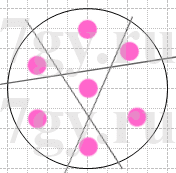
На торте кондитер расположил семь кремовых розочек (рис.38). Как тремя прямолинейными разрезами разделить торт на семь порций, на каждой из которых была бы одна розочка?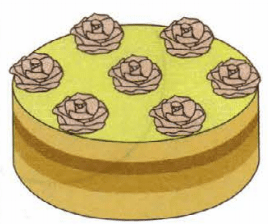
Решение
Задание №725
Вычислите:
1) $7^2=7\ast7=49$
2) $0,4^2=0,4\ast0,4=0,16$
3) $1,2^2=1,2\ast1,2=1,44$
4) $(\frac13)^2=\frac13\ast\frac13=\frac19$
5) $(2\frac29)^2=\frac{20}9\ast\frac{20}9=\frac{400}{81}=4\frac{76}{81}$