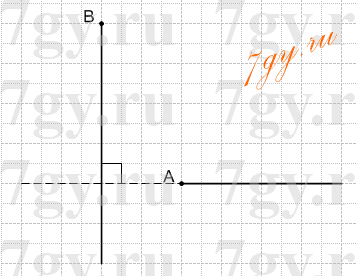Ответы к странице 254
Задание №1223
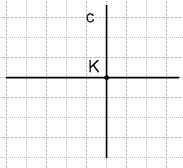
Проведите прямую c и отметьте точку K, принадлежащую ей. Проведите через точку K прямую, перпендикулярную прямой c.
Решение
Задание №1224
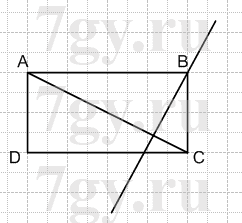
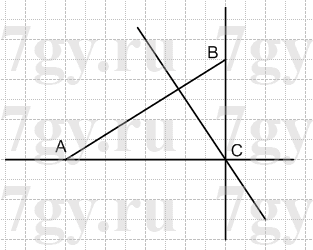
Начертите прямоугольник ABCD, соедините точки A и C. Проведите через точку B прямую, перпендикулярную прямой AC.
Решение
Задание №1225
Начертите треугольник:
1) остроугольный;
2) тупоугольный;
3) прямоугольный.
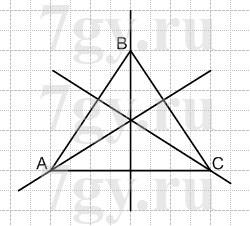
Проведите через каждую вершину треугольника прямую, перпендикулярную противоположной стороне.
Решение
1)
2)
3)
Задание №1226
Начертите угол ABK, градусная мера которого равна:
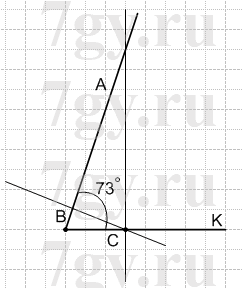
1) 73°;
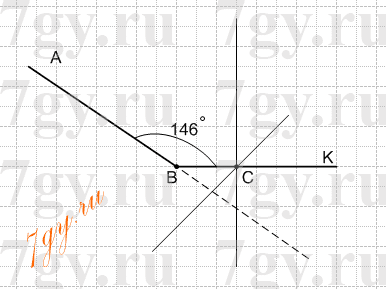
2) 146°.
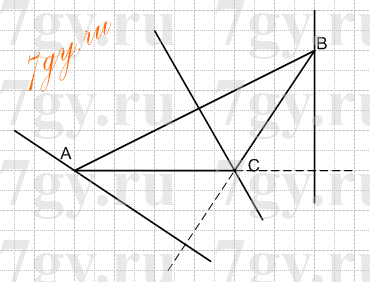
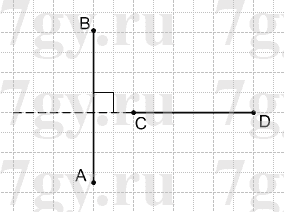
Отметьте на луче BK точку C и проведите через нее прямые, перпендикулярные прямым AB и BK.
Решение
1)
2)
Задание №1227
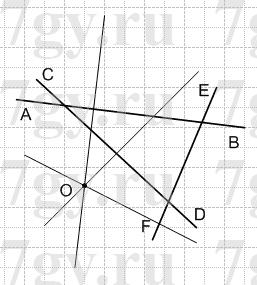
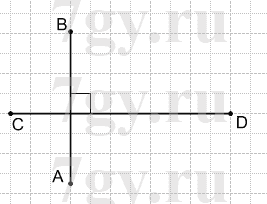
Перерисуйте в тетрадь рисунок 121. Проведите через точку O прямые, перпендикулярные прямым AB, CD и EF.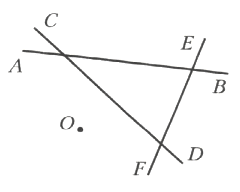
Решение
Задание №1228
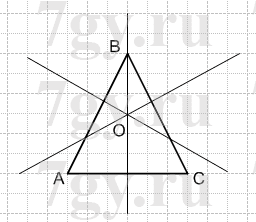
Начертите остроугольный треугольник и отметьте внутри него точку. Проведите через эту точку прямые, перпендикулярные сторонам треугольника.
Решение
Задание №1229
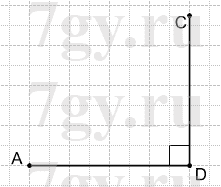
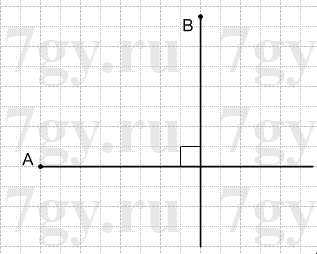
Начертите четырехугольник ABCD, в котором:
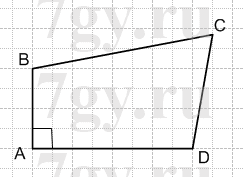
1) AB⊥AD;
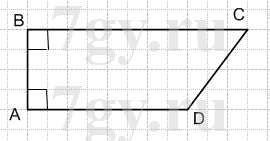
2) AB⊥AD, AB⊥BC;
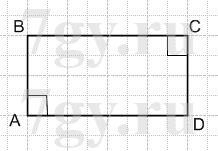
3) AB⊥AD, BC⊥CD.
Решение
1)
2)
3)
Задание №1230
С помощью угольника определите, какие из прямых, изображенных на рисунке 122, перпендикулярны.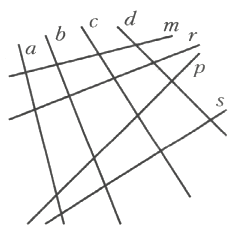
Решение
a⊥m; b⊥r; c⊥s; d⊥p.
Задание №1231
Начертите два перпендикулярных отрезка так, чтобы они:
1) пересекались;
2) не имели общих точек;
3) имели общий конец.
Решение
1)
2)
3)
Задание №1232
Начертите два перпендикулярных луча так, чтобы они:
1) пересекались;
2) не имели общих точек.
Решение
1)
2)
Задание №1233
На рисунке 123 AB⊥CD, ∠MOC + ∠BOK = 130°, COK = 42°. Найдите:
1) ∠MOK;
2) ∠MOD.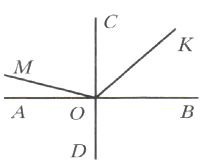
Решение
1) Так как, AB⊥CD, то ∠COB = 90°, тогда:
∠KOB = ∠COB − ∠COK = 90° − 42° = 48°.
∠MOC + ∠BOK = 130°, тогда:
∠MOC = 130° − ∠BOK = 130° − 42° = 82°.
∠MOK = ∠MOC + ∠COK = 82° + 42° = 124°.
Ответ: ∠MOK = 124°
2) Так как, AB⊥CD, то ∠COB = 90°; ∠AOC = 90°, тогда:
∠AOB = ∠COB + ∠AOC = 90° + 90° = 180°;
∠AOM = ∠AOB − (∠MOC + ∠BOK) − ∠COK = 180° − 130° − 42° = 8°.
Так как, AB⊥CD, то ∠AOD = 90°, тогда:
∠MOD = ∠AOD + ∠AOM = 90° + 8°= 98°.
Ответ: ∠MOD = 98°